
- •«Введение в теорию надёжности»
- •1 Основные определения и количественные показатели
- •1.1 Надёжность объектов как комплексное свойство
- •1.2 Классификация отказов и предельное состояние объекта
- •1.3 Единичные и комплексные показатели надёжности
- •Средняя наработка на отказ – это отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки
- •1.4.1 Состав и общие правила задания требований на надёжность
- •1.5 Аналитические зависимости между показателями надёжности
- •2 Расчёт показателей надёжности
- •2.1.1 Прикидочный расчёт надёжности
- •2.1.2 Ориентировочный расчёт надёжности
- •2.1.3 Окончательный (коэффициентный) расчёт надёжности
- •2.1.4 Методика оценки безотказности технических средств
- •2.2 Расчёт структурной надёжности резервированных систем
- •2.2.1 Классификация методов резервирования
- •2.2.2 Расчёт надёжности при общем и раздельном резервировании
- •2.2.7 Расчёт надёжности по схеме «гибели-размножения»
- •2.3 Расчёт надёжности программных средств
- •2.3.1 Основные определения теории надёжности программного обеспечения
- •2.3.2 Методика оценки числа оставшихся ошибок в программе
- •2.3.3 Методика расчёта интенсивности обнаружения ошибок в зависимости от времени эксплуатации программы
- •2.3.5 Рекомендации по повышению надёжности программного обеспечения
- •3 Расчёт показателей надёжности при проектировании
- •3.1 Расчёт функциональной надёжности системы
- •3.1.1 Определение термина «функциональная надёжность» системы
- •3.2 Анализ качества структурной схемы
- •3.2.1 Показатели качества структурной схемы
- •Распределение требований к надёжности элементов схемы
- •3.4 Сравнение различных методов повышения надёжности системы
- •3.4.1 Краткое описание основных методов повышения надёжности
- •3.4.2 Примеры, иллюстрирующие сложность проблемы повышения надёжности
2.3.2 Методика оценки числа оставшихся ошибок в программе
Оценка
потенциального числа ошибок в ПО перед
началом разработки программы может
быть проведена путём расчёта количества
независимых входных и выходных величин
 ,
потенциального объёма программы и
возможного числа ошибок в ней. Приведём
примеры анализа входных и выходных
данных.
,
потенциального объёма программы и
возможного числа ошибок в ней. Приведём
примеры анализа входных и выходных
данных.
Пример
1. Рассматривается
система контроля посадки самолётов в
условиях ограниченной видимости. В
состав системы входят курсовой радиомаяк,
глиссадный радиомаяк, ответчик
радиодальномера. Входными величинами
системы являются : три пространственные
координаты (азимут, угол места, дальность),
всего количество координат равно
 Три информационных эталонных канала,
т.е. -
четыре координаты самолёта (высота,
путевая скорость, крен, тангаж).
Три информационных эталонных канала,
т.е. -
четыре координаты самолёта (высота,
путевая скорость, крен, тангаж).
Всего есть сорок входных величин. Выходных величин для каждого информационного канала будет четыре (три пространственные координаты плюс время), т.е. всего 12 независимых величин.
Решение.

потенциальный объём программы равен
 бит,
бит,
а количество потенциальных ошибок в ПО равно

Пример 2. Определить характеристики программного обеспечения для боевой космической станции (БКС) системы противоракетной обороны (ПРО) типа стратегической оборонной инициативы президента США Рейгана. БКС должна быть рассчитана на перехват около 1000 целей с расстояния примерно 400 км.
Решение. Для перехвата необходимо рассчитать местоположение целей, их скорость, расстояние до них и условные параметры прицеливания. Упростим задачу и попытаемся получить оценку снизу. Поэтому не будем рассматривать задачи распознавания целей и согласования полученных данных с моделью боевой ситуации. Будем рассматривать предельно простой случай полной децентрализации, когда процессор управляющего компьютера непосредственно подключён к датчикам БКС и обрабатывает данные о координатах наблюдаемых объектов с целью вычислить их положение на момент перехвата. Полагаем, что на одном экране БКС появляется одновременно не более 20 целей, а 30 последовательных измерений положения объекта и его скорости статистически достаточно для получения необходимой точности и выбора наилучшего момента поражения одной цели.
Пусть
для определения природы объекта
необходимо измерить пять величин и на
экране измеряются две координаты для
каждого из 20 объектов. Таким образом,
количество входных величин оказывается
равным
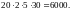
Выходные
величины программы – это угловые
координаты целей и расстояние до них.
Для 20 целей количество выходных величин
составляет

Итак,

что даёт для потенциального объёма программы значение равное
 бит.
бит.
Расчёты показывают, что для создания такого объёмного ПО требуется около 1012 чел. - часов. Потенциальное количество ошибок в этом гигантском по объёму ПО для языков различного уровня равно:

На устранение такого огромного количества ошибок может потребоваться значительно больше времени, чем на создание самого программного обеспечения. Поэтому разработка ПО такого большого объёма сомнительна.
Выполним расчёт потенциального количества ошибок в ПО перед началом комплексной отладки. Уточнение значения числа ошибок можно было бы провести путём прямого подсчёта значений и . Однако для программ, написанных на языке низкого уровня это сделать затруднительно. Возможен иной подход, который рассмотрим для ПО при условиях примера 1. Особенностью этого ПО является то, что оно написано на Ассемблере.
Значение
складывается из числа команд
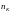 ,
используемой системы команд и из числа
отдельных подпрограмм
,
используемой системы команд и из числа
отдельных подпрограмм
 .
В ПО примера использовалось 45 различных
операторов, число подпрограмм составило
157. Таким образом,
.
В ПО примера использовалось 45 различных
операторов, число подпрограмм составило
157. Таким образом,

Количество
операндов
равно сумме
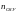 (различные
переменные и массивы данных, используемых
в ПО); плюс количество локальных меток
(различные
переменные и массивы данных, используемых
в ПО); плюс количество локальных меток
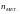 и констант
и констант
 .
Для облегчения подсчёта
используют имеющееся распределение
памяти оперативного запоминающее
устройства (ОЗУ), при этом подходе
исключается повторяемость соответствующих
операндов. Число локальных меток
подсчитывают по тексту программы на
Ассемблере слева от мнемонической
записи команды. Таким способом
гарантируется не повторяемость меток,
а общепринятая табуляция облегчает
подсчёт. Сложнее сосчитать число
различных констант, которые оформляются
в массивы числовых данных и используются
при адресации в Ассемблере. Поэтому по
тексту программы считают лишь число
констант, заведомо помещающихся в одном
байте. Как правило, они выделяются в
тексте и вероятность их совпадения
очень мала. К значению этой величины
прибавляют 256 – число возможных байтовых
констант. Для рассматриваемого ПО
указанные величины имеют следующие
значения :
.
Для облегчения подсчёта
используют имеющееся распределение
памяти оперативного запоминающее
устройства (ОЗУ), при этом подходе
исключается повторяемость соответствующих
операндов. Число локальных меток
подсчитывают по тексту программы на
Ассемблере слева от мнемонической
записи команды. Таким способом
гарантируется не повторяемость меток,
а общепринятая табуляция облегчает
подсчёт. Сложнее сосчитать число
различных констант, которые оформляются
в массивы числовых данных и используются
при адресации в Ассемблере. Поэтому по
тексту программы считают лишь число
констант, заведомо помещающихся в одном
байте. Как правило, они выделяются в
тексте и вероятность их совпадения
очень мала. К значению этой величины
прибавляют 256 – число возможных байтовых
констант. Для рассматриваемого ПО
указанные величины имеют следующие
значения :

Тогда
 82
+ 334 + 280 + 256 = 952.
82
+ 334 + 280 + 256 = 952.
Полученные
значения
и
можно сопоставить с расчётными значениями,
которые определены из решения уравнений
Холстеда для

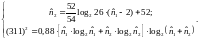
В
результате решения
 Эти значения можно полагать приемлемыми
(отличие от реального ПО составляет
11,0 % и 10,5 %).
Эти значения можно полагать приемлемыми
(отличие от реального ПО составляет
11,0 % и 10,5 %).
Рассчитаем длину программы
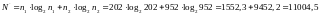
и определим объём программы
 бит.
бит.
Уточнённая оценка переданного количества ошибок в ПО равна:

Оценка
 отличается от полученной ранее
отличается от полученной ранее
 = 168 лишь на 12 % и по своему смыслу является
более близкой к реальности.
= 168 лишь на 12 % и по своему смыслу является
более близкой к реальности.
