
- •«Введение в теорию надёжности»
- •1 Основные определения и количественные показатели
- •1.1 Надёжность объектов как комплексное свойство
- •1.2 Классификация отказов и предельное состояние объекта
- •1.3 Единичные и комплексные показатели надёжности
- •Средняя наработка на отказ – это отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки
- •1.4.1 Состав и общие правила задания требований на надёжность
- •1.5 Аналитические зависимости между показателями надёжности
- •2 Расчёт показателей надёжности
- •2.1.1 Прикидочный расчёт надёжности
- •2.1.2 Ориентировочный расчёт надёжности
- •2.1.3 Окончательный (коэффициентный) расчёт надёжности
- •2.1.4 Методика оценки безотказности технических средств
- •2.2 Расчёт структурной надёжности резервированных систем
- •2.2.1 Классификация методов резервирования
- •2.2.2 Расчёт надёжности при общем и раздельном резервировании
- •2.2.7 Расчёт надёжности по схеме «гибели-размножения»
- •2.3 Расчёт надёжности программных средств
- •2.3.1 Основные определения теории надёжности программного обеспечения
- •2.3.2 Методика оценки числа оставшихся ошибок в программе
- •2.3.3 Методика расчёта интенсивности обнаружения ошибок в зависимости от времени эксплуатации программы
- •2.3.5 Рекомендации по повышению надёжности программного обеспечения
- •3 Расчёт показателей надёжности при проектировании
- •3.1 Расчёт функциональной надёжности системы
- •3.1.1 Определение термина «функциональная надёжность» системы
- •3.2 Анализ качества структурной схемы
- •3.2.1 Показатели качества структурной схемы
- •Распределение требований к надёжности элементов схемы
- •3.4 Сравнение различных методов повышения надёжности системы
- •3.4.1 Краткое описание основных методов повышения надёжности
- •3.4.2 Примеры, иллюстрирующие сложность проблемы повышения надёжности
2.3.1 Основные определения теории надёжности программного обеспечения
Основными терминами, которые используются в теории надёжности программного обеспечения, являются следующие: программная ошибка; число оставшихся в программе ошибок, которые будут переданы далее пользователю; интенсивность обнаружения ошибок (функция риска); «прогон» программы; отказ программы; вероятность безотказной работы программного обеспечения.
Основная трудность определения термина «программная ошибка» состоит в том, что ошибка в программе – это по своей сути функция самой программы и того, чего ожидает от неё пользователь. Перечислим основные проявления, которые можно идентифицировать как ошибку:
появление при программировании ошибочного операнда или операции;
несоответствие выполняемых ПО функций требованиям спецификаций, либо ошибка в спецификации, которая приводит к ошибке при выполнении операции ПО;
ошибки вычислительного характера (например, переполнение);
исправление ПО, улучшающее его взаимодействие с пользователем.
К программным ошибкам не относят исправления, создающие или уничтожающие временные программные «заглушки» на отсутствующую или не корректную программу, а так же перетрансляцию программы, вызванную накопившимися исправлениями. Количество оставшихся в ПО или переданных ошибок – это потенциальное число ошибок в ПО, которое может быть обнаружено в нём на последующих этапах его жизненного цикла после исправлений, внесённых на данном этапе. Это количество ошибок будем обозначать символом В.
Введём
интенсивность обнаружения ошибок или
функцию риска r(t),
которая определяется отношением числа
обнаруженных ошибок к промежутку
времени, за который
эти ошибки были обнаружены. Для
интенсивности обнаружения ошибок
справедливы все формулы, которые известны
из теории надёжности. В отличие от
интенсивности отказов
 функция риска убывает по мере обнаружения
и исправления ошибок. Если предположить,
что
функция риска убывает по мере обнаружения
и исправления ошибок. Если предположить,
что
 остаётся постоянной между моментами
обнаружения и исправления ошибок,
уменьшаясь скачкообразно на постоянную
величину в момент обнаружения ошибок,
то для простоты целесообразно полагать
её пропорциональной количеству оставшихся
ошибок
остаётся постоянной между моментами
обнаружения и исправления ошибок,
уменьшаясь скачкообразно на постоянную
величину в момент обнаружения ошибок,
то для простоты целесообразно полагать
её пропорциональной количеству оставшихся
ошибок
 ,
(2.80)
,
(2.80)
где
 - число обнаруженных ошибок на данном
этапе.
- число обнаруженных ошибок на данном
этапе.
Дифференцируя уравнение (2.80) по времени получим

где
 - есть функция риска
.
Если решить дифференциальное уравнение
- есть функция риска
.
Если решить дифференциальное уравнение
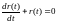 ,
с начальными условиями
,
с начальными условиями
 то
то
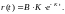 (2.81)
(2.81)
Обозначим
 Тогда уравнение (2.81) можно переписать
в виде
Тогда уравнение (2.81) можно переписать
в виде
 (2.82)
(2.82)
Функцию
риска зададим дискретно, придав интервалу
времени заданное значение (день, неделя,
месяц). Логарифмируя уравнение (2.82) для
выбранных значений времени
 ,
получим систему уравнений вида
,
получим систему уравнений вида
 (2.83)
(2.83)
Расчёт экспоненциальной регрессии даёт следующие выражения для её коэффициентов
 (2.84)
(2.84)
 (2.85)
(2.85)
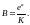 (2.86)
(2.86)
Программа для расчёта экспоненциальной регрессии приведена ниже в 2.3.3.
Будем под удельной интенсивностью обнаружения ошибок в ПО понимать следующую функцию времени:
 (2.87)
(2.87)
где
 -
число ошибок в ПО, которые исправлены
к моменту времени t
;
-
число ошибок в ПО, которые исправлены
к моменту времени t
;
 - число команд в программе. Приближенно
можно полагать, что
- число команд в программе. Приближенно
можно полагать, что
 (2.88)
(2.88)
здесь
 - разрядность команды;
- разрядность команды;
 - объем программы по Холстеду, что будет;
В
– число оставшихся ошибок в ПО к моменту
t
= 0; К –
коэффициент пропорциональности. Величины
В
и К
являются неизвестными.
- объем программы по Холстеду, что будет;
В
– число оставшихся ошибок в ПО к моменту
t
= 0; К –
коэффициент пропорциональности. Величины
В
и К
являются неизвестными.
Рассмотрим два периода отладки программы Т1 и Т2 такие, что Т1 < Т2. Пусть n1 и n2 соответственно количество ошибок в ПО, обнаруженных в каждом из периодов. Тогда для среднего времени безошибочной (безотказной) работы в каждом из периодов можно записать следующие выражения:
 (2.89)
(2.89)
 (2.90)
(2.90)
Разделив первое равенство на второе, после преобразований можно получить:
 (2.91)
(2.91)
где
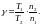
Подставив полученное значение B в формулу для среднего времени безотказной работы в первом периоде отладки программы, можем определить коэффициент пропорциональности
 . (2.92)
. (2.92)
Определив
В
и К,
можно для любого момента времени
вычислить значение удельной интенсивности
обнаружения ошибок в ПО
 и вероятность безотказной работы,
полагая, что время исправной работы
подчинено экспоненциальному закону
распределения.
и вероятность безотказной работы,
полагая, что время исправной работы
подчинено экспоненциальному закону
распределения.
Прогоном программы называют совокупность действий, включающую в себя:
ввод возможной комбинации Еi входных данных;
выполнение расчёта по программе, которая заканчивается получением результата F(Ei) или отказом.
Для определенного набора входных данных отклонение результата от заданного значения F`(Ei), полученное в результате выполнения программы, находится в допустимых пределах
 (2.93)
(2.93)
а
для всех остальных Ei
, образующих подмножество
 ,
выполнение программы не обеспечивает
приемлемого результата, т.е.
,
выполнение программы не обеспечивает
приемлемого результата, т.е.
 >
> (2.94)
(2.94)
События, описываемые неравенством (2.94), называются отказами программы.
Методика статистической оценки вероятности отказа ПО за n независимых прогонов программы является традиционной и формально включает в себя оценку
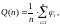 (2.95)
(2.95)
где
 если
выполняется неравенство (2.93);
если
выполняется неравенство (2.93);
 если
выполняется неравенство (2.94).
если
выполняется неравенство (2.94).
Обозначим
через
 допустимую относительную погрешность
оценки вероятности отказа. Тогда
необходимое число независимых прогонов
программы
n
должно быть пропорционально величине
допустимую относительную погрешность
оценки вероятности отказа. Тогда
необходимое число независимых прогонов
программы
n
должно быть пропорционально величине
 где
где
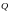 - заданное значение вероятности отказа.
Так, при
- заданное значение вероятности отказа.
Так, при
 и значении
и значении
 число независимых прогонов должно быть
не меньше
число независимых прогонов должно быть
не меньше

Такое количество прогонов трудно реализовать на практике и обычно обращаются к другим методам оценки вероятности отказа ПО. Зная вероятность отказа, нетрудно вычислить вероятность безотказной работы ПО.
Для
проверки надёжности ПО используются
методы проверки статистических гипотез
и, в частности, последовательный анализ
Вальда. Сопоставим дихотомической
переменной
 значение 1,
если выполняется (2.94), и значение 0, если
выполняется (2.93 ). Тогда результат
прогонов образует выборку случайных
величин
значение 1,
если выполняется (2.94), и значение 0, если
выполняется (2.93 ). Тогда результат
прогонов образует выборку случайных
величин
 Обозначим вероятность того, что
Обозначим вероятность того, что
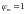 ,
т.е. программа отказывает, как Р; а
вероятность Р0
того. что
,
т.е. программа отказывает, как Р; а
вероятность Р0
того. что
 принимает значение 0, а программа
исправна. Тогда выбор значения
принимает значение 0, а программа
исправна. Тогда выбор значения
Р0 =0,99 означает, что в серии из 100 прогонов вероятно в среднем появление одного отказа.
Применение
последовательного анализа позволяет
существенно ограничить число испытаний
на надёжность ПО и не налагает жёстких
требований на закон распределения
случайной величины
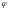 .
Практическое применение последовательного
анализа будет продемонстрировано ниже.
.
Практическое применение последовательного
анализа будет продемонстрировано ниже.
Большое значение для получения приближенных оценок показателей надёжности ПО имеют так называемые метрики Холстеда. Эти же метрики позволяют численно оценить и другие характеристики ПО: длину программы, её объём, уровень программы, её интеллектуальное содержание, длительность разработки и т.п. Метрики прошли серьезную практическую апробацию и показали приемлемую для практических расчётов точность. Рассмотрим сущность метода Холстеда.
Для любой программы можно определить:
число различных операций
 ,
например,
,
например,
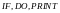 и др.;
и др.;общее число всех операндов
 (переменных и констант);
(переменных и констант);общее число всех операций

общее число всех операндов

Тогда
словарь программы есть
 ,
а длина реализации составляет
,
а длина реализации составляет
 Длина программы в этом случае равна
Длина программы в этом случае равна
 (2.96)
(2.96)
а
объём программы
 (2.97)
(2.97)
потенциальный объём программы
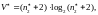 (2.98)
(2.98)
где
 минимальное
число различных операндов (точнее, число
независимых входных и выходных величин).
минимальное
число различных операндов (точнее, число
независимых входных и выходных величин).
Потенциальный
объём
 - минимально возможный объём определённого
алгоритма. Уровень программы L
определяется через отношение потенциального
объёма к объёму программы
- минимально возможный объём определённого
алгоритма. Уровень программы L
определяется через отношение потенциального
объёма к объёму программы
 (2.99)
(2.99)
Работа по программированию Е оценивается как суммарное число элементарных мысленных отличий между элементами, необходимых для генерации программы:
 (2.100)
(2.100)
Уровень языка позволяет оценивать преимущество языка более высокого уровня по сравнению со своим предшественником и определяется выражением
 (2.101)
(2.101)
что позволяет иначе выразить характеристики Е и V:
 (2.102)
(2.102)
 (2.103)
(2.103)
В таблице 2.2 приведены численные значения для языков различного уровня.
Таблица 2.2 – Численные значения уровня языка
-
Язык
Уровень
Ассемблер
0,88
Бейсик
1,14
Английский
2,16
Трудоемкость разработки программного обеспечения определяется по формуле
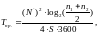 чел. - часов;
(2.104)
чел. - часов;
(2.104)
где
 - параметр Страуда, т.е. время, которое
необходимо человеческому мозгу для
определения существенного отличия
между двумя элементами, оценивается
значением 5-20 существенных различий в
секунду.
- параметр Страуда, т.е. время, которое
необходимо человеческому мозгу для
определения существенного отличия
между двумя элементами, оценивается
значением 5-20 существенных различий в
секунду.
Замечено, что при разработке сложных программ трудоёмкость их создания и количество выявленных при отладке ошибок существенно возрастают. При этом число переданных ошибок пропорционально объёму программы.
 (2.105)
(2.105)
или
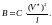 (2.106)
(2.106)
Коэффициент
пропорциональности С
определяют, исходя из следующих
соображений. В соответствии с эмпирическим
законом Д. Миллера «7
2»
для
 определим, что
определим, что
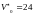 ,
а для английского языка с учётом (2.100)
получим
,
а для английского языка с учётом (2.100)
получим

что
позволяет оценить коэффициент С
как

однако для языков более низкого уровня правильнее оценивать С, используя выражение более общего вида
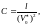 (2.107)
(2.107)
что,
в частности, для Ассемблера даёт значение
 Таким образом,
Таким образом,
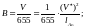 (2.108)
(2.108)
или в более общей форме
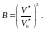 (2.109)
(2.109)
Значения величин и могут быть определены из результатов анализа ПО или косвенно путем решения уравнений Холстеда, если известны значения и :
 (2.110)
(2.110)
