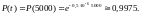- •«Введение в теорию надёжности»
- •1 Основные определения и количественные показатели
- •1.1 Надёжность объектов как комплексное свойство
- •1.2 Классификация отказов и предельное состояние объекта
- •1.3 Единичные и комплексные показатели надёжности
- •Средняя наработка на отказ – это отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки
- •1.4.1 Состав и общие правила задания требований на надёжность
- •1.5 Аналитические зависимости между показателями надёжности
- •2 Расчёт показателей надёжности
- •2.1.1 Прикидочный расчёт надёжности
- •2.1.2 Ориентировочный расчёт надёжности
- •2.1.3 Окончательный (коэффициентный) расчёт надёжности
- •2.1.4 Методика оценки безотказности технических средств
- •2.2 Расчёт структурной надёжности резервированных систем
- •2.2.1 Классификация методов резервирования
- •2.2.2 Расчёт надёжности при общем и раздельном резервировании
- •2.2.7 Расчёт надёжности по схеме «гибели-размножения»
- •2.3 Расчёт надёжности программных средств
- •2.3.1 Основные определения теории надёжности программного обеспечения
- •2.3.2 Методика оценки числа оставшихся ошибок в программе
- •2.3.3 Методика расчёта интенсивности обнаружения ошибок в зависимости от времени эксплуатации программы
- •2.3.5 Рекомендации по повышению надёжности программного обеспечения
- •3 Расчёт показателей надёжности при проектировании
- •3.1 Расчёт функциональной надёжности системы
- •3.1.1 Определение термина «функциональная надёжность» системы
- •3.2 Анализ качества структурной схемы
- •3.2.1 Показатели качества структурной схемы
- •Распределение требований к надёжности элементов схемы
- •3.4 Сравнение различных методов повышения надёжности системы
- •3.4.1 Краткое описание основных методов повышения надёжности
- •3.4.2 Примеры, иллюстрирующие сложность проблемы повышения надёжности
2.2.2 Расчёт надёжности при общем и раздельном резервировании
Общее резервирование с постоянно включённым резервом (с целой кратностью). Упрощающие предположения: а) отказы элементов системы описываются простейшими потоками отказов; б) резервируемые и резервные элементы равно надёжны. Итак, заданы число основных элементов в системе N; вероятность безотказной работы i –го элемента, кратность резервирования.
1
2
N
0
1
2
N
1
1
2
N
m
Рисунок 2.2 – Схема общего резервирования с постоянно включённым
резервом
Для системы без резервирования при независимых отказах вероятность безотказной работы равна
 (2.12)
(2.12)
а вероятность отказа равна
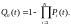 (2.13)
(2.13)
Вероятность отказа системы с общим резервированием составляет
 (2.14)
(2.14)
Так
как элементы системы равно надёжны, то
 или
или
 (2.15)
(2.15)
где
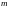 - число резервированных цепей.
- число резервированных цепей.
Для экспоненциального закона надёжности


где
 - интенсивность отказов любой из
- интенсивность отказов любой из
 систем.
систем.
 (2.16)
(2.16)
 (2.17)
(2.17)
Средняя наработка до отказа равна
 (2.18)
(2.18)
плотность вероятности
 (2.19)
(2.19)
интенсивность отказов
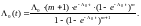 (2.20)
(2.20)
Раздельное резервирование с постоянно включённым резервом.
Схема этого вида резервирования имеет вид
1
N
2
0
1
2
N
1
2
N
m
Рисунок 2.3 – Схема раздельного резервирования с постоянно
включённым резервом
Вероятность того, что произойдёт отказ системы из-за отказов функциональной группы элементов i – го типа, равна произведению вероятностей отказа i – го элемента и всех элементов его резервирующих
 (2.21)
(2.21)
а вероятность безотказной работы функциональной группы элементов равна
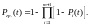 (2.22)
(2.22)
Если основные и резервные элементы равно надёжны, то
 (2.23)
(2.23)
Полагая, что функциональные группы в системе соединены последовательно, и принимая их отказы независимыми в совокупности, получаем
 (2.24)
(2.24)
Принимая экспоненциальный закон надёжности, и полагая, как и ранее, что все элементы системы равно надёжны, вероятность безотказной работы системы можно рассчитать по формуле
 (2.25)
(2.25)
где интенсивность отказов равна
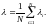 (2.26)
(2.26)
Выражение для средней наработки до отказа имеет вид
 (2.27)
(2.27)
Общее резервирование замещением с целой кратностью.
При резервировании замещением необходимо устройство, которое включает резервные элементы взамен отказавших основных элементов. Само это устройство часто называют переключателем, и оно обладает определённой вероятностью отказа. По этой причине вероятность отказа системы резервированной замещением вычисляют по формуле
 (2.28)
(2.28)
1
2
N
1
2
N N N
1
1
2
N
m
Рисунок 2.4 – Схема общего резервирования замещением
Вероятность безотказной работы системы определяется по рекуррентному соотношению
 (2.29)
(2.29)
где
 вероятности безотказной работы
резервированной системы кратности
и
соответственно;
вероятности безотказной работы
резервированной системы кратности
и
соответственно;
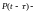 вероятность безотказной работы основной
системы в течение времени
вероятность безотказной работы основной
системы в течение времени
 ;
;
 плотность вероятности отказов
резервированной системы кратности
в момент времени
плотность вероятности отказов
резервированной системы кратности
в момент времени
 .
Рекуррентная формула (2.29) позволяет
получить расчётные соотношения для
устройств любой кратности резервирования.
Для получения этих формул необходимо
выполнить интегрирование в правой
части, подставив вместо
.
Рекуррентная формула (2.29) позволяет
получить расчётные соотношения для
устройств любой кратности резервирования.
Для получения этих формул необходимо
выполнить интегрирование в правой
части, подставив вместо
 и
и
 их выражения в соответствии с выбранным
законом распределения и состоянием
резерва.
их выражения в соответствии с выбранным
законом распределения и состоянием
резерва.
При экспоненциальном законе надёжности и ненагруженном состоянии резерва
 (2.30)
(2.30)
 (2.31)
(2.31)
где
 интенсивность отказов и средняя наработка
до первого отказа основного (не
резервированного) элемента системы.
интенсивность отказов и средняя наработка
до первого отказа основного (не
резервированного) элемента системы.
При экспоненциальном законе надёжности и недогруженном состоянии резерва
 (2.32)
(2.32)
 (2.33)
(2.33)
здесь
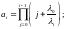
 интенсивность отказов резервного
элемента
интенсивность отказов резервного
элемента
до замещения.
При
нагруженном состоянии резерва формулы
для
 и
и
 совпадают с формулами для общего
резервирования с постоянно включённым
резервом и целой кратностью.
совпадают с формулами для общего
резервирования с постоянно включённым
резервом и целой кратностью.
Раздельное резервирование замещением с целой кратностью. Вероятность безотказной работы системы вычисляется по формуле
 (2.34)
(2.34)
где
 вероятность безотказной работы системы
из-за отказов элементов i
– го типа, которые резервированы по
способу замещения. Вычисляется
вероятность безотказной работы системы
из-за отказов элементов i
– го типа, которые резервированы по
способу замещения. Вычисляется
 по формулам общего резервирования
замещением (2.29), (2.30), (2.32).
по формулам общего резервирования
замещением (2.29), (2.30), (2.32).
Пример
1. Вероятность
безотказной работы преобразователя
частоты переменного тока, питающего
электродвигатель переменного тока
главного циркуляционного насоса
технологического аппарата в течение t
= 1000 часов равна 0,95. Для повышения
надёжности системы управления насосом
есть ещё один такой же преобразователь
частоты, который включается в работу
при отказе первого. Определить вероятность
безотказной работы системы из двух
преобразователей, полагая, что
переключающее устройство является
абсолютно надёжным, и построить графики
зависимости от времени функций
 и
и

Решение. Из условия задачи, очевидно, что имеет место общее резервирование замещением кратностью =1 с не нагруженным резервом.

по
условию задачи
 ;
отсюда
;
отсюда
 ;
а вероятность безотказной работы системы
;
а вероятность безотказной работы системы


Для
t
= 1000 часов и





Графики
и
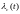 имеют следующий вид
имеют следующий вид



 5,0
5,0


 3,0
3,0




 1,0
1,0
 ,
час
,
час
1,6 3,2 4,8 6,4 8,0
Пример 2.
Логический контроллер имеет вероятность
безотказной работы
 Для
повышения надёжности он резервируется
ещё одним таким же контроллером в
состоянии нагруженного резерва,
переключающий элемент имеет вероятность
безотказной работы
Для
повышения надёжности он резервируется
ещё одним таким же контроллером в
состоянии нагруженного резерва,
переключающий элемент имеет вероятность
безотказной работы
 .
Определить, каким должно быть значение
вероятности безотказной работы
переключателя, чтобы вероятность
безотказной работы системы была не ниже
0,98
.
.
Определить, каким должно быть значение
вероятности безотказной работы
переключателя, чтобы вероятность
безотказной работы системы была не ниже
0,98
.
Решение. Так как раздельное резервирование замещением с нагруженным резервом соответствует общему резервированию замещением, то вероятность безотказной работы системы следует вычислять по формуле

Решим полученное неравенство


отсюда вероятность безотказной работы переключателя равна или больше

2.2.3 Расчёт надёжности при общем резервировании с дробной кратностью и нагруженным резервом
При резервировании с дробной кратностью эксплуатация резервированной системы возможна при условии, если количество исправных элементов не меньше необходимого для нормальной работы.
1
2
N





1
k
Рисунок 2.5 - Схема общего резервирования с дробной кратностью
Кратность
резервирования определяется из
соотношения
 где
где
 - общее число элементов расчёта
резервированной системы;
- общее число элементов расчёта
резервированной системы;
 - число элементов, которое необходимо
для нормальной работы;
- число элементов, которое необходимо
для нормальной работы;
 - число резервных элементов.
- число резервных элементов.
Количество
замещений, не нарушающих работу
резервированной системы в целом, не
может быть больше
 .
В предположении абсолютной надёжности
переключающих устройств и равной
надёжности элементов системы с
интенсивностью отказов
средняя наработка до отказа такой
резервированной системы равна
.
В предположении абсолютной надёжности
переключающих устройств и равной
надёжности элементов системы с
интенсивностью отказов
средняя наработка до отказа такой
резервированной системы равна
 (2.35)
(2.35)
Система
в течение времени
 будет работать безотказно, если за это
время произойдёт хотя бы одно из
следующих событий:
будет работать безотказно, если за это
время произойдёт хотя бы одно из
следующих событий:
 - все элементы исправны;
- все элементы исправны;
 - один элемент отказал,
- один элемент отказал,
 элементов исправны;
элементов исправны;
 элементов отказали,
элементов отказали,
 элементов исправны;
элементов исправны;
 элементов отказали, а
элементов исправны. Количество различных
вариантов равно числу сочетаний
элементов отказали, а
элементов исправны. Количество различных
вариантов равно числу сочетаний

 (2.36)
(2.36)
В этом случае вероятность безотказной работы системы определяется соотношением
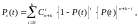 (2.37)
(2.37)
где - вероятность безотказной работы элемента при условии, что все элементы равно надёжны.
Пример 3. В системе защиты от превышения уровня в технологическом аппарате применена схема группирования уровнемеров «3 из 5», т.е. результат измерения считается верным по показаниям трёх приборов. Определить вероятность безотказной работы этой системы, если переключатель имеет вероятность безотказной работы .
Решение.
Для мажоритарного резервирования по
схеме «3 из 5»
= 3,
= 2. Тогда
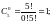


для
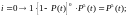

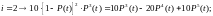
а вероятность безотказной работы системы будет равна

2.2.4 Логико-вероятностные методы расчёта резервированных систем
Основные правила преобразования логических высказываний
Логико-вероятностный метод расчёта надёжности состоит в описании схемы системы при помощи аппарата математической логики с последующим использованием выводов теории вероятностей для определения показателей надёжности. При расчётах характеристик надёжности наиболее часто применяют следующие правила для преобразования сложных высказываний.
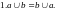
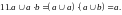


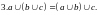
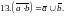

 (2.38)
(2.38)


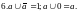

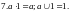



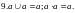

Логическую функцию сложного высказывания необходимо привести к минимальной бесповторной форме, «арифметизировать» её и затем заменить высказывание его вероятностью. Логические уравнения, содержащие операции дизъюнкции (логическое суммирование), конъюнкции (логическое умножение) и отрицания, можно привести к арифметическому виду, если заменить логические операции арифметическими по следующему правилу:
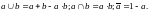 (2.39)
(2.39)
Пример
4. Определить
вероятность сложного высказывания
 ,
если вероятность высказываний
,
если вероятность высказываний
 и
и
 равна 0,8.
равна 0,8.
Решение.
 арифметизируем логическую функцию:
арифметизируем логическую функцию:
 Заменим события
Заменим события
 их вероятностями и получим
их вероятностями и получим
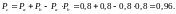
Расчёт надёжности, основанный на использовании
параллельно-последовательных структур
Схема надёжности для элементов, которые соединены параллельно, имеет вид



Рисунок 2.5 - Схема расчёта надёжности параллельно соединённых
элементов
Условие
работоспособности системы: система
работоспособна, если работоспособен
элемент
 или элемент
или элемент
 ,
или элемент
,
или элемент
 .
Этому условию соответствует логическая
формула
.
Этому условию соответствует логическая
формула

 .
.
Минимизируем это выражение
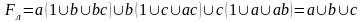 .
.
Примечание.

 .
.
Арифметизируем
выражение для логического высказывания
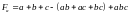 и заменим события
и заменим события
 их вероятностями:
их вероятностями:

Вероятность
безотказного состояния системы,
состоящего из
параллельно соединённых элементов,
равна
Среднее время работы до отказа (2.40)
 (2.41)
Интенсивность отказов системы,
состоящей из
параллельно соединённых элементов с
интенсивностью отказов
(2.41)
Интенсивность отказов системы,
состоящей из
параллельно соединённых элементов с
интенсивностью отказов
 (Пуассоновский поток событий) равна
(Пуассоновский поток событий) равна

 (2.42)
(2.42)
Расчётные формулы для элементов, соединённых последовательно
Рисунок 2.6 - Расчётная схема надёжности для элементов,
соединённых последовательно
Условие работоспособности системы следующее: система работоспособна, если работоспособен элемент , элемент , элемент .
Этому
условию соответствует логическая
формула
 Арифметизируем
эту логическую формулу
Арифметизируем
эту логическую формулу
 Заменяем
события
их вероятностями
Заменяем
события
их вероятностями
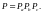
Для
системы, состоящей из
 последовательно соединённых элементов,
показатели надёжности таковы:
последовательно соединённых элементов,
показатели надёжности таковы:
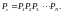
 (2.43)
(2.43)
Пример 5. Определить вероятности состояний системы, схема которой и граф состояний изображены на рисунке 2.7, если интенсивность отказов элементов 1 и 2 равна 0,02; а интенсивность восстановления равна 1,0 .
1
2
С0
С1
С2
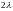


Рисунок 2.7 - Расчётная схема резервированной системы и
её граф состояния
Решение.
Итак, интенсивность переходов системы
в состояния С0
, С1
, С2
равны:

Финальные вероятности для цепи Маркова вычисляются по формулам
 ;
;
 .
.
Вероятность
состояния С0:

Вероятность
состояния С1
равна
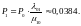
Вероятность
состояния С2
равна

Способы преобразования сложных структур
К этим преобразованиям относятся: преобразование с эквивалентной заменой «треугольника» на «звезду» и обратно; и разложение сложной структуры по базовому элементу.
Сущность способа преобразования сложных структур с эквивалентной заменой «треугольника» на «звезду» заключается в том, что соединение одной конфигурации заменяют на соединение другой конфигурации, более простое с точки зрения расчёта надёжности. При этом подбираются такие характеристики нового соединения, чтобы его показатели надёжности были такими же, что и до преобразования.
Допустим, что
необходимо заменить «треугольник»
«звездой» при условии, что вероятность
отказа элемента
равна
 ,
элемента
равна
,
элемента
равна
 ,
элемента
равна
,
элемента
равна
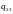 .
Переход к соединению «звездой» не
должен изменять надёжность цепей 1-2,
1-3, 2-3.
.
Переход к соединению «звездой» не
должен изменять надёжность цепей 1-2,
1-3, 2-3.
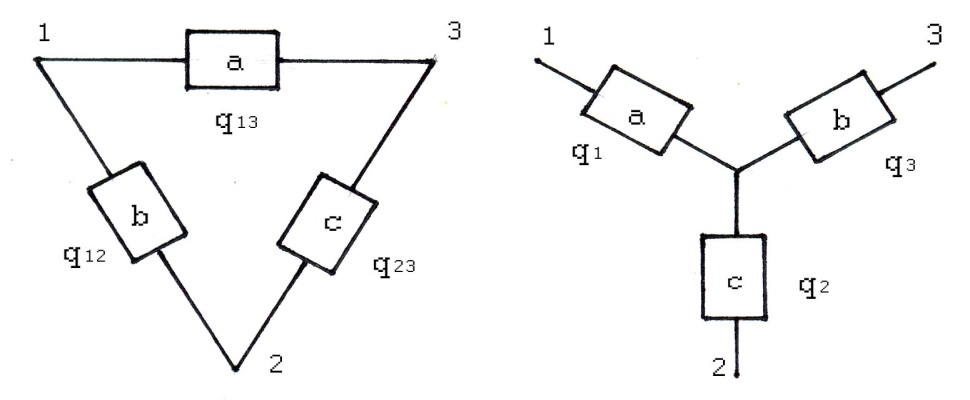
Поэтому
значения вероятности отказов элементов
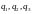 должны удовлетворять следующей системе
уравнений:
должны удовлетворять следующей системе
уравнений:
 (2.44)
(2.44)
Если
пренебречь произведениями вида
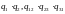 и другими, то в результате решение
системы уравнений (2.46) может быть записано
в виде
и другими, то в результате решение
системы уравнений (2.46) может быть записано
в виде
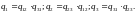 (2.45)
(2.45)
Для
обратного преобразования «звезды» в
«треугольник» используют соотношения
 (2.47)
(2.47)
Пример 6. Определить вероятность безотказной работы системы, структурная схема которой изображена ниже, если известно, что вероятность безотказной работы каждого из элементов системы равна 0,9 .
1
3

5

2
4
Решение. Преобразуем соединение элементов 1-2-5 из «треугольника» в «звезду» и определим эквивалентные значения вероятностей отказов для новых элементов :

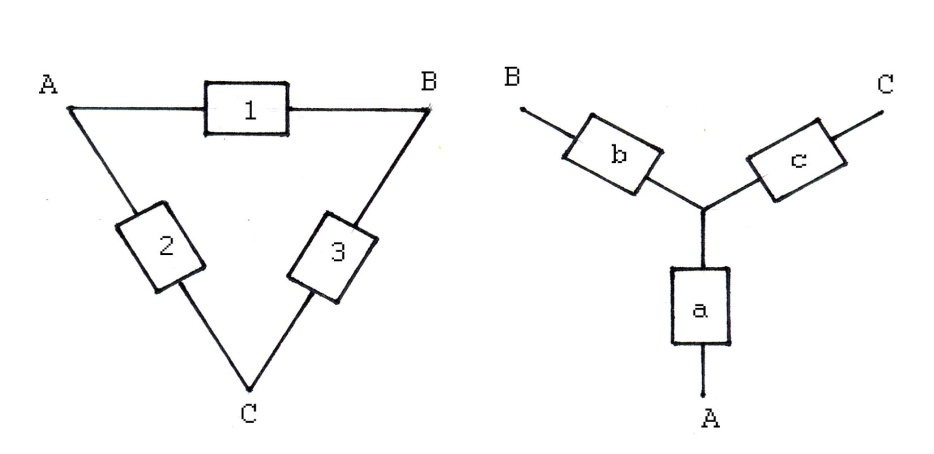
Определим
значения вероятностей исправного
состояния элементов эквивалентной
схемы:
 Схема эквивалентной системы имеет вид
Схема эквивалентной системы имеет вид
3
4
Вероятность безотказной работы эквивалентной системы равна

Преобразование с помощью разложения сложной структуры
по некоторому базовому элементу
Этот способ преобразования сложных структур основан на использовании теоремы о сумме вероятностей несовместных событий. В системе выбирают базовый элемент (или группу базовых элементов) и решают задачу в два этапа: 1) сначала допускают, что базовый элемент находится в работоспособном состоянии (сигнал через него проходит); 2) затем допускают, что базовый элемент находится в состоянии отказа (сигнал через него не проходит).
Для этих случаев, представляющих собой два несовместных события, исходная структурная схема преобразуется в две новые схемы. В одной из них вместо базового элемента ставится «короткое замыкание», а во второй – «разрыв». Вычисляется вероятность безотказной работы каждой из полученных структур и они перемножаются: первая - на вероятность безотказного состояния базового элемента; вторая – на вероятность отказа базового элемента. Полученные произведения суммируются. Эта сумма равна искомой вероятности безотказной работы исходной системы.
Пример 7. Решить пример 6 методом разложения сложной структуры.
1
3
5

2
4
В
качестве базового элемента принимаем
элемент 5. «Закоротим» базовый элемент
и присоединим его с вероятностью
безотказной работы
 к полученной структуре последовательно.
В результате получим новую схему
к полученной структуре последовательно.
В результате получим новую схему
1
3
5

2
4
Произведём
«обрыв» базового элемента. К полученной
структуре присоединяют последовательно
базовый элемент, имеющий вероятность
отказа
 .
В результате получим схему вида
.
В результате получим схему вида
1
3
2
4


Искомая вероятность равна сумме вероятностей безотказной работы полученных схем, каждая из которых является параллельно-последовательной:
 =
0,9(0,9 + 0,9 – 0,92)2
+ 0,1(2
0,92
– 0,94)
= 0,978 .
=
0,9(0,9 + 0,9 – 0,92)2
+ 0,1(2
0,92
– 0,94)
= 0,978 .
Расчёт надёжности иерархической структуры передачи данных
Допустим, что необходимо определить для информационной системы, схема которой приведена ниже, вероятность передачи информации от верхнего элемента «0» до четырёх, трёх, двух, одного из нижних элементов и для полного отказа в передаче информации. Вероятность передачи информации определяется только аппаратной надёжностью каналов связи. Вероятность исправного состояния канала связи равна 0,9 .
 6
6

0 2 5

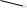 4
4
1 3
Решение. Обозначив 1,2,3,4,5,6 – события, заключающиеся в том, что соответствующие каналы исправны, запишем условие для передачи информации к четырём, трём, двум, одному и ни к одному из нижних элементов системы. Далее определим искомые вероятности в последовательности, которая указана в условии задачи.
А. Определение вероятности того, что информация дойдёт до четырёх нижних элементов.
Логическая функция работоспособности имеет вид
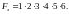
Арифметизируем
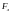 :
:

Заменим события их вероятностями

Б. Определение вероятности того, что информация дойдёт до трёх нижних звеньев из четырёх.
Логическая функция работоспособности имеет вид:


=

Арифметизируем логическую функцию и заменим события их вероятностями:

=
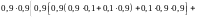

=

В. Определим вероятность того, что информация дойдёт до двух нижних элементов из четырёх.
Логическая функция работоспособности такова:



Бесповторная форма логической функции имеет вид


арифметизируя логическую функцию и заменяя события их вероятностями, получим

+

Г. Определим вероятность того, что информация дойдёт до одного нижнего элемента из четырёх:


=

=
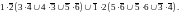

Д.
Определим вероятность того, что
информация не дойдёт ни до одного нижнего
элемента системы из четырёх. Логическая
функция работоспособности равна
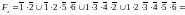
=
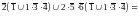
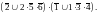
Арифметизируем :



Проверка:

Расчёт надёжности системы передачи информации
с дополнительными обходными каналами



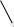 4
4
2
1 3
5
Рисунок 2.8 - Структурная схема системы передачи информации
с дополнительными обходными каналами
Логическая функция работоспособности системы имеет вид:

Арифметизируем
:
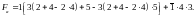
Заменим события их вероятностями, тогда получим


Пусть
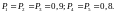
В
этом случае

2.2.5 Расчёт надёжности систем при «скользящем» резервировании
Из
теории передаточных функций известно,
что получить динамические характеристики
системы по известным динамическим
характеристикам отдельных звеньев
просто лишь для параллельного соединения
звеньев (сумма характеристик каждого
звена). Для цепочки последовательного
соединения звеньев необходимо
последовательное применение интеграла
Дюамеля (свёртки) к каждому звену.
Например, при последовательном включении
двух звеньев с динамическими
характеристиками
 и
и



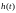
переходная характеристика системы может рассматриваться как реакция второго звена с на входное воздействие, которым для этого звена является переходная характеристика первого звена . Применив для вычисления интеграл Дюамеля, получим
 (2.46)
(2.46)
где
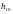 - значение переходной функции
для
- значение переходной функции
для

Этот же подход применяют для расчёта надёжности систем при «скользящем» резервировании, которое изображается следующими схемами
1
N
1
N
1
1
N
2
2
б)
а)
Рисунок 11 - Схема «скользящего» резервирования однотипными» (а) и
не однотипными элементами (б).
Вероятность безотказной работы при «скользящем» резервировании определяется соотношением


+...+

...+ (2.47)
(2.47)
где
 - число элементов основной системы;
- количество резервных элементов;
- число элементов основной системы;
- количество резервных элементов;
 - вероятность безотказной работы одного
элемента в течение времени
- вероятность безотказной работы одного
элемента в течение времени
 плотность распределения вероятности
безотказной работы одного из основных
элементов в момент времени
плотность распределения вероятности
безотказной работы одного из основных
элементов в момент времени

Здесь не учитывается вероятность безотказной работы переключающих элементов. Для экспоненциального закона распределения вероятности безотказной работы можно получить следующее соотношение
 (2.48)
(2.48)
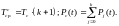 (2.49)
(2.49)
Индекс
относится к не резервированной системе,
кратность резервирования в этом случае

Рассмотрим,
в качестве примера, расчёт вероятности
безотказной работы восстанавливаемой
системы, состоящей из основного и
не нагруженных резервных элементов,
если распределение вероятности
безотказной работы элементов системы
не является экспоненциальным. Она может
быть вычислена путём решения следующего
рекуррентного уравнения
 .
.
Значение
 определяется рекуррентно, а
определяется рекуррентно, а
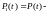 это
вероятность безотказной работы одного
элемента;
это
вероятность безотказной работы одного
элемента;
 вероятность восстановления, являющаяся
частным случаем функции Грина. Для
важного в практике случае, когда
вероятность восстановления, являющаяся
частным случаем функции Грина. Для
важного в практике случае, когда
 (дублирование), а время восстановления
элемента
(дублирование), а время восстановления
элемента
 и средняя наработка до первого отказа
и средняя наработка до первого отказа
 удовлетворяют выражению
удовлетворяют выражению
 (2.50)
(2.50)
значение
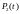 можно вычислить по приближённой формуле
можно вычислить по приближённой формуле
 (2.51)
(2.51)
где
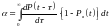 .
Если
.
Если
 а
а
 то
то
 Т –
наработка на отказ одного не резервированного
элемента системы
Т –
наработка на отказ одного не резервированного
элемента системы
т.е.,
для
 (2.52)
(2.52)
 .
.
Для
 ,
соответственно,
,
соответственно,
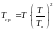
Итак, если применяется скользящее резервирование с числом резервных элементов и восстановлением отказавших элементов для системы, состоящей из однотипных элементов, а её наработка на отказ в не резервированном состоянии равна = 1000 часов, то можно рассчитать наработку до отказа для резервированной системы по формуле:
 (2.53)
(2.53)
Тогда
при одном резервном элементе (системе)
наработка на отказ будет превышать
 часов, если
часов, если
 часа, что вполне реально.
часа, что вполне реально.
2.2.6 Расчёт надёжности при учёте последействия отказов
Приведённые выше формулы, кроме формул для общего резервирования с целой кратностью и для экспоненциального закона надёжности при не нагруженном состоянии резерва, могут быть использованы только в случаях, когда справедливо допущение об отсутствии последействия отказов.
Элементы резервированных систем в ряде случаев могут иметь два вида отказов: «обрыв» и «короткое замыкание». Вероятность безотказной работы системы в этом случае вычисляют, суммируя вероятности всех благоприятных гипотез, не приводящих к отказу:
 (2.54)
(2.54)
где
- число благоприятных гипотез,
 - вероятность j-й
благоприятной гипотезы, которая вычислена
с учётом двух видов отказа. При этом
- вероятность j-й
благоприятной гипотезы, которая вычислена
с учётом двух видов отказа. При этом
 (2.55)
(2.55)
здесь
 - вероятности возникновения «обрыва»
и «короткого замыкания». Для
экспоненциального закона надёжности
вероятность безотказной работы равна
- вероятности возникновения «обрыва»
и «короткого замыкания». Для
экспоненциального закона надёжности
вероятность безотказной работы равна
 (2.56)
(2.56)
Пример 9. Определить вероятность безотказной работы схемы соединения диодов
Интенсивность
отказов диода
 вероятность отказов типа «пробой»
(короткое замыкание)
вероятность отказов типа «пробой»
(короткое замыкание)
 время непрерывной работы схемы
время непрерывной работы схемы
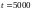 часов.
часов.
Решение. Рассмотрим для вышеприведенной схемы благоприятные гипотезы:
Все диоды исправны

Один любой диод отказал, остальные исправны

Один любой диод отказал по «обрыву», а другой – по «короткому замыканию», оставшиеся два диода исправны

Два диода отказали по «обрыву», остальные диоды – исправны

Два диода отказали по «короткому замыканию», остальные – исправны

6. Один диод
исправен, два отказали по «обрыву», а
один – по «короткому замыканию»
7. Один диод
исправен, два – отказали по «короткому
замыканию», один диод отказал по «обрыву»

Суммируя вероятности гипотез, получим вероятность безотказной работы системы в виде

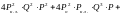
+
Для
 получим
получим

Вероятность
безотказной работы одного диода равна