
- •Методическое пособие по элементарной математике
- •Составители:
- •§1 Множества.
- •§2 Числовая ось
- •§3 Модуль действительного числа
- •§4 Степени и корни
- •§5 Функции и их свойства
- •§ 6 Линейные преобразования графика функций
- •§7 Обзор элементарных функций
- •§8 Многочлены
- •§9 Корни алгебраического уравнения
- •§10 Рациональные неравенства
- •§11 Прогрессии
§8 Многочлены
Многочленом от
называется выражения вида:
![]() ,
,![]()
![]() ;
- старшая степень многочлена;
;
- старшая степень многочлена;
![]() - коэффициенты многочлена,
- аргумент многочлена. Если
- коэффициенты многочлена,
- аргумент многочлена. Если
![]() ,
то
,
то
![]() .
Число
.
Число
![]() ,
обращающее многочлен в 0, называется
корнем многочлена
,
обращающее многочлен в 0, называется
корнем многочлена
![]() .
.
Рассмотрим действие
деление многочленов если существует
такой многочлен
![]() ,
что
,
что
![]() ,
где
,
где
![]() ,
то говорят, что
,
то говорят, что
![]() делится на
и
- делитель, а
делится на
и
- делитель, а
![]() - частное.
- частное.
![]() .
.
![]() - делитель,
- делитель,
![]() - частное.
- частное.
Более общая операция
называется делением с остатком:
![]() ,
где
,
где
![]() .
.
![]() - остаток, от деления
на
.
Другая запись:
- остаток, от деления
на
.
Другая запись:
![]() - правильный.
- правильный.
Пример.
![]() - неправильная дробь. Выделим целую
часть: для этого поделим
- неправильная дробь. Выделим целую
часть: для этого поделим
![]() на
на
![]() .
.

1)сначала делим старшей степени и результат записываем в частное
2)умножаем
![]() на делитель и вычитаем из делимого.
на делитель и вычитаем из делимого.
Процесс повторяется пока степень делимого не будет меньше степени делителя.
![]()
Теорема.
Если
![]() ,
то для любого числа
,
то для любого числа
![]() справедливо равенство
справедливо равенство
![]() .
.
Пример.
![]() .
Найти
.
Найти
![]() .
.
Решение.
![]() .
.
![]() (*)
(*)
1 способ.
подставляя в обе
части равенства значения аргумента
![]()
![]() .
.
2 способ. нахождения
![]() .
.
Согласно определению
равенства многочленов справа должен
стоять многочлен первой степени с теми
же коэффициентами, что и у многочлена
стоящего слева:
![]()
Решая систему
находим:
![]() .
.
§9 Корни алгебраического уравнения
Число
![]() - является корнем многочлена
если
.
- является корнем многочлена
если
.
Задача. Найти все
корни многочлена это задача: решить
уравнение
![]() .
.
![]() при
при
![]() .
.
![]() при
при
![]() ,
согласно теореме Виета
,
согласно теореме Виета
![]() .
.
При решении
алгебраических уравнений степени больше
(равно 3) полезна теорема Безу, следствие
из которой: если
корень многочлена
![]() ,
то этот многочлен делится без остатка
на разность
,
то этот многочлен делится без остатка
на разность
![]() ;
частное от деления
на
есть многочлен степень которого равна
;
частное от деления
на
есть многочлен степень которого равна
![]() .
Целые корни многочлена
.
Целые корни многочлена
![]() с целыми коэффициентами ищутся среди
делителей свободного члена
с целыми коэффициентами ищутся среди
делителей свободного члена
![]() .
.
Теорема.
Каждое алгебраическое уравнение п-ой
степени
![]() имеет ровно п
корней.
имеет ровно п
корней.
§10 Рациональные неравенства
Рациональные неравенства – это неравенства вида:
1)
![]() или 2)
или 2)
![]() Э,
где
Э,
где
![]() и
и
![]() некоторые многочлены.
некоторые многочлены.
Поскольку
![]() .
.
![]() ,
то для решения рациональных неравенств
удобно применить метод интегралов.
,
то для решения рациональных неравенств
удобно применить метод интегралов.
![]() .
Раскладывая числитель на множители.
Подбором среди делителей свободного
члена числителя находим что корень
многочлена
.
Раскладывая числитель на множители.
Подбором среди делителей свободного
члена числителя находим что корень
многочлена
![]() .
.
Деля данный
многочлен углом на
![]() получаем
получаем
![]() .
.
Исходное неравенство равносильно системе:
![]()
Решая 1-ое неравенство методом интервалов:
корни многочлена, стоящего в левой части неравенства разбивают ось на интервалы знакопостоянства многочлена;
определяем знак многочлена в каждом из интервалов;
пишем ответ.
Выкалывая точки
![]() и
и
![]() .
Получаем окончательно:
.
Получаем окончательно:
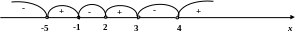
![]() .
.
§11 Прогрессии
Арифметическая прогрессия (а.п.)
если
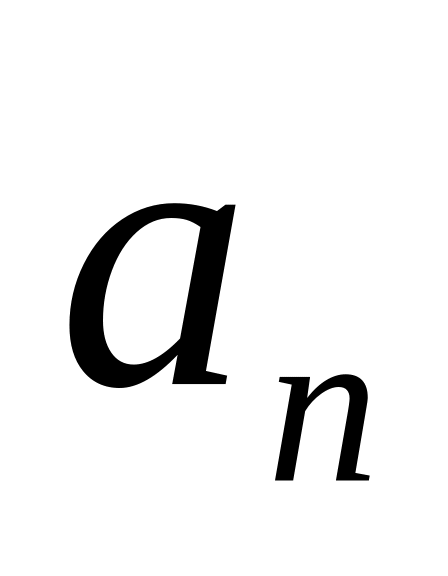 есть п-й
член,
есть п-й
член,
 разность и
разность и
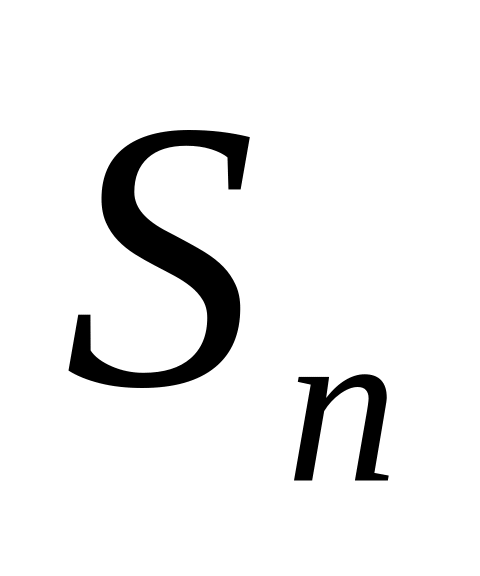 - сумма п
первых членов а.п., то
- сумма п
первых членов а.п., то
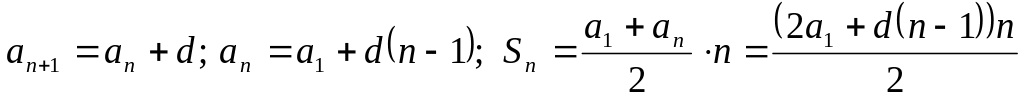 .
а.п. возрастает, если
.
а.п. возрастает, если
 ,
убывает, если
,
убывает, если
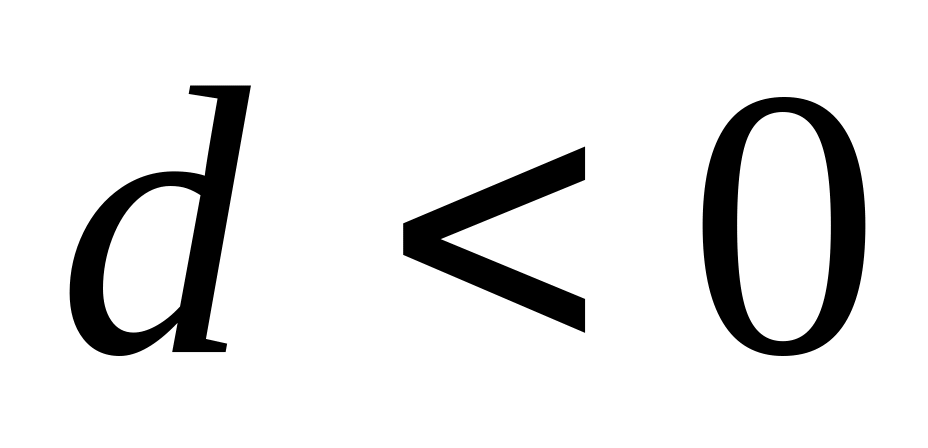 .
.Для каждого члена а.п., начиная со второго выполняется равенство
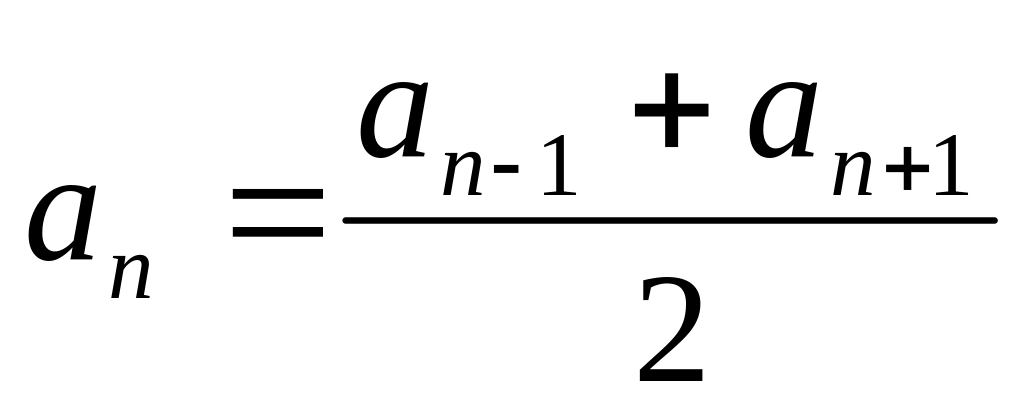 .
.
Геометрическая прогрессия (г.п.)
если
 есть п-ый
член,
есть п-ый
член,
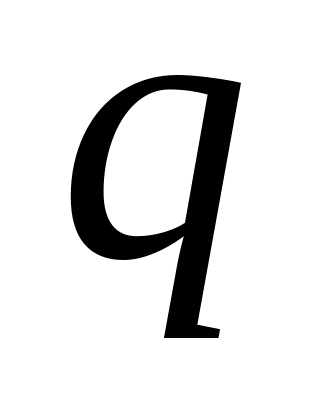 -
знаменатель,
- сумма п
первых членов прогрессии, то:
-
знаменатель,
- сумма п
первых членов прогрессии, то:
 .
.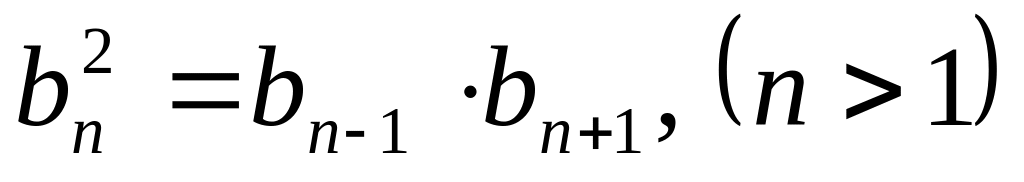
Бесконечно
убывающая геометрическая прогрессия
![]()
![]() .
.
