Министерство образования и науки РФ
Государственное образовательное учреждение
высшего профессионального образования
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Р.Е. Алексеева
Кафедра «Прикладная математика»
Методическое пособие по элементарной математике
Нижний Новгород 2011
Составители:
УДК 517
МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ/НГТУ;cост.: Т.А. Горева, Л.Н. Камаева -Н. Новгород, 2011 –15 с.
Научный редактор Л.Н. Камаева
Редактор С.Н. Митяков
Компьютерный набор: Т.О. Парфенова
Учебное пособие содержит подробное изложение лекционного материала по элементарной математике. Приведены примеры.
Подписано в печать . Формат 60х84 1/16. Бумага газетная.
Печать офсетная. Усл. п. л. . Уч.-изд. л. . Тираж 300 экз. Заказ .
Нижегородский государственный технический университет.
Типография НГТУ.603950, Нижний Новгород, ул.Минина, 24. © Нижегородский государственный
технический университет
им. Р.Е. Алексеева, 2011
§1 Множества.
Множество
называется множеством натуральных
чисел, обозначается буквой
.
Наибольшим
общим делителем
(НОД) двух натуральных чисел
и
называется наибольший из общих делителей
этих чисел.
Наименьшим общим кратным (НОК) двух натуральных чисел и называется наименьшее число из общих кратных этих чисел.
Пример.
.
Целыми
числами
называются числа
множество целых чисел и обозначается
;
.
Рациональным
множеством
называется множество чисел
,
где
,
а
;
а
несократимая дробь.
Иррациональное
множество
.
Иррациональные
числа бывают двух типов: алгебраические,
которые являются корнем некоторого
многочлена и неалгебраические:
.
Иррациональные числа записываются в
виде бесконечных непериодических
десятичных дробей.
Объединение
множеств рациональных и иррациональных
чисел называется множество
действительных чисел
и обозначается
.
§2 Числовая ось
Числовой осью называется ось, на которой выбрана точка начала отсчета и единица длины.
Можно установить взаимно однозначное соответствие между действительными числами и точками на числовой оси.
§3 Модуль действительного числа
Определение:
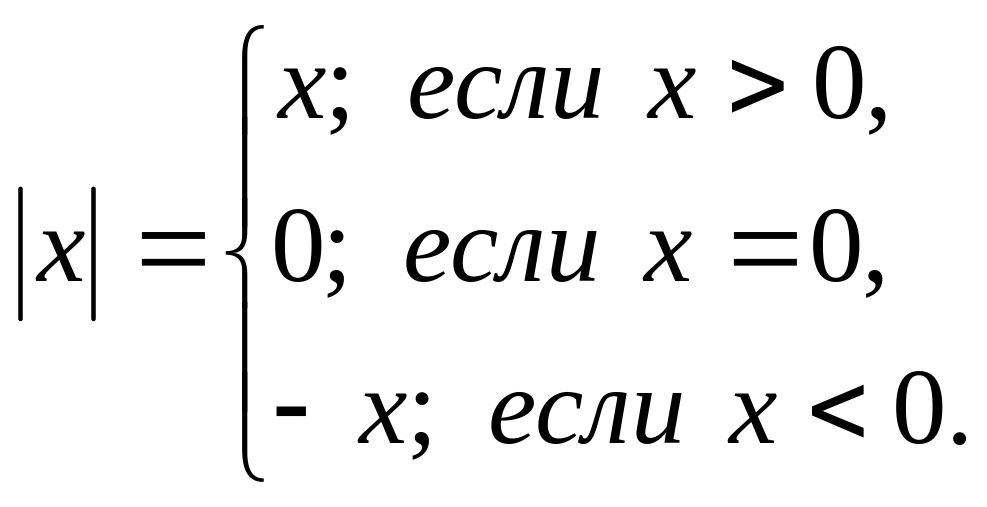
Геометрически
есть расстояние от точки
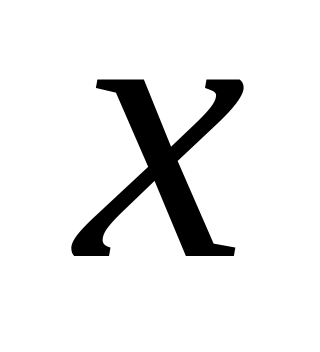на числовой оси до начала отсчета –
точки
.
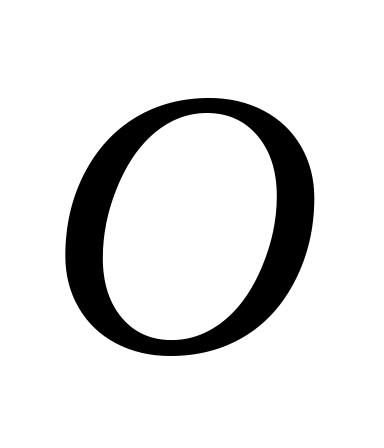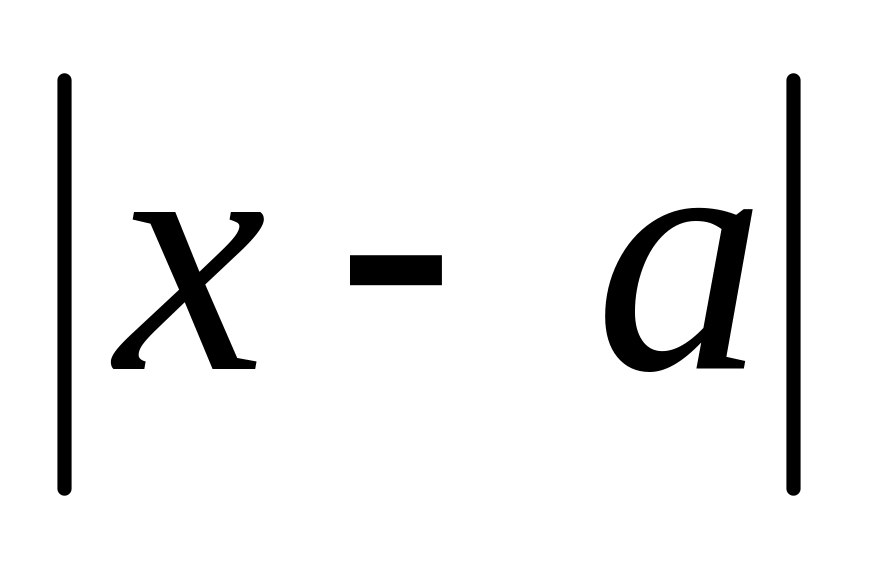есть расстояние
между точками
и
числовой оси.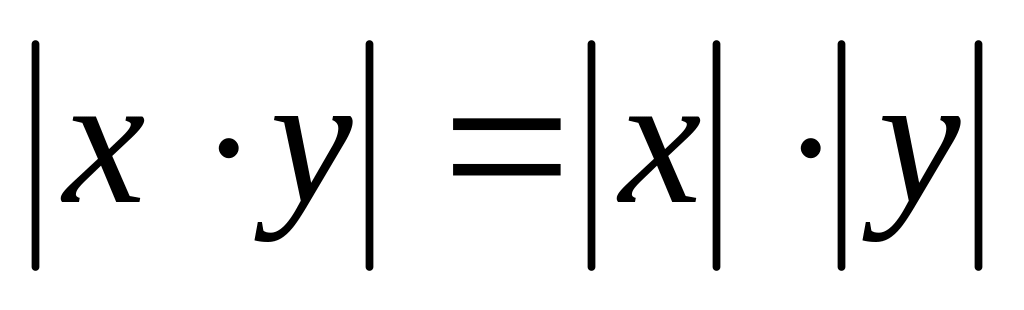
;
;
;
;
.
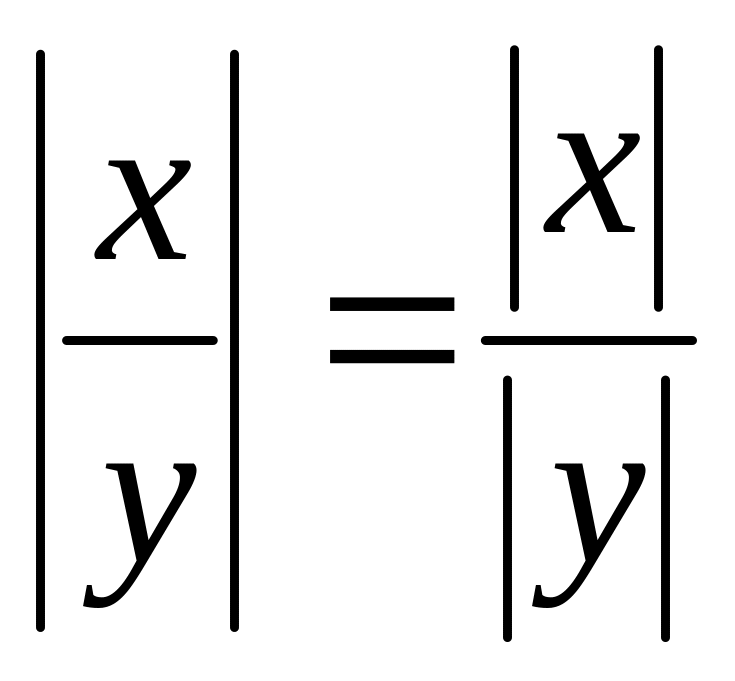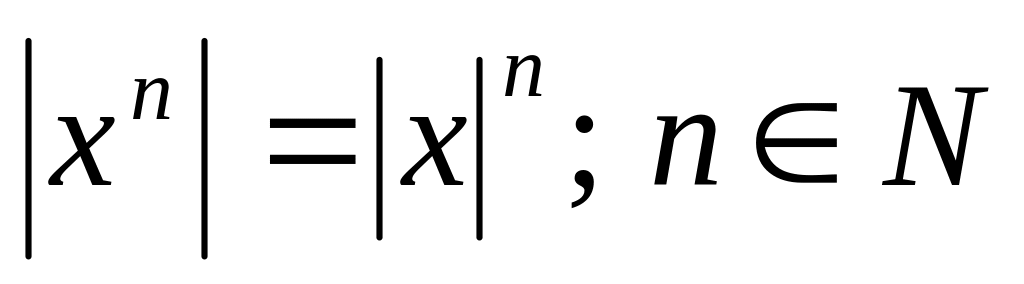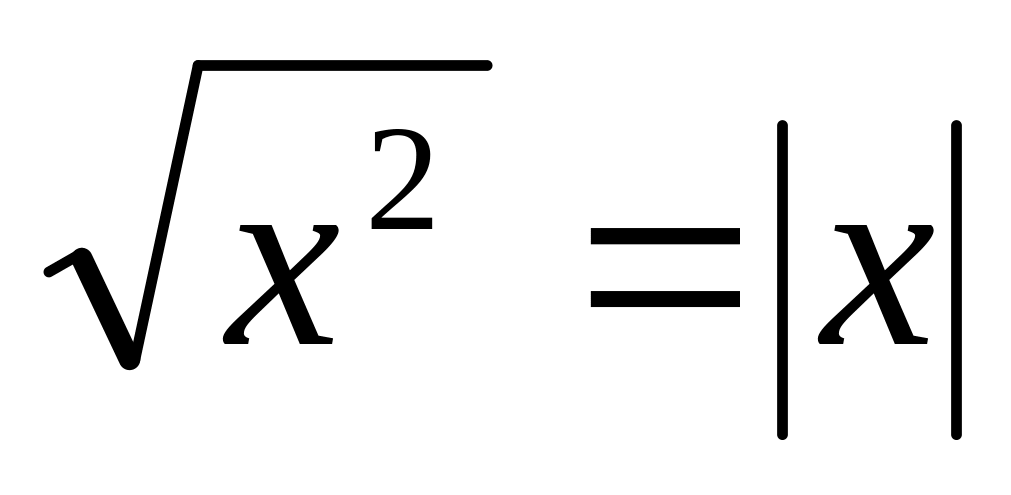Используя свойство
№3 легко решаются неравенство
.
Найти
,
находящиеся на расстоянии от точки
меньше, чем
.
§4 Степени и корни
Определение
.
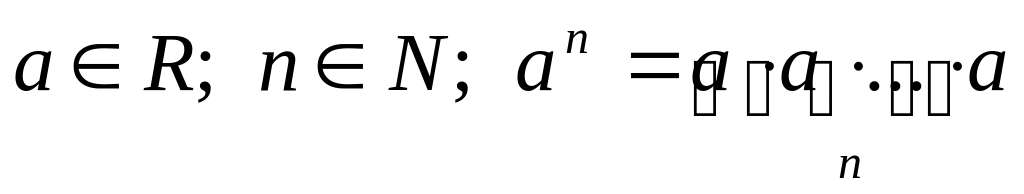- основание степени,
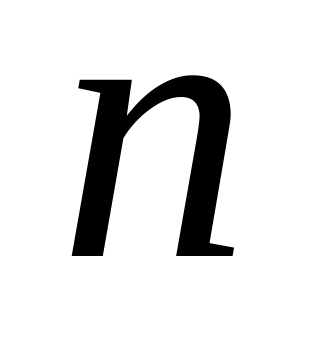- показатель степени.
-
не определено.
,
если
- четное.
знак равносильности.
,
при
- нечетном.
.
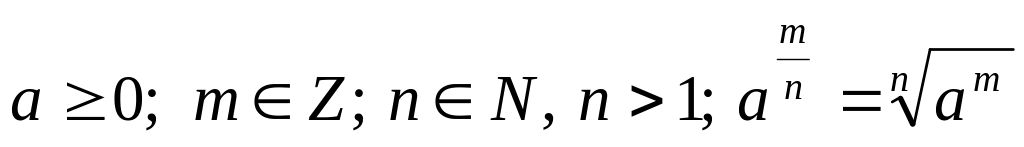Правила действия с радикалами
.
.
Пример.
Правила действия со степенями
.
Формулы сокращенного умножения
.
Чтобы избавиться от иррациональности в числителе (знаменателе) дроби надо умножить и числитель и знаменатель на множитель, используя формулы сокращенного умножения.
Пример.
1)
;
2)
.
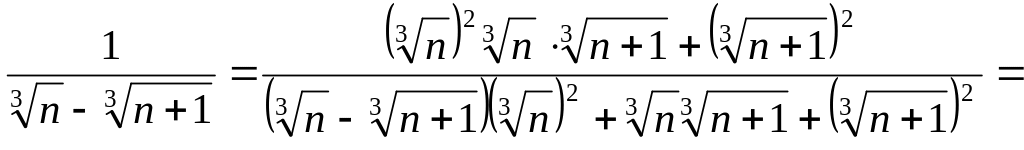
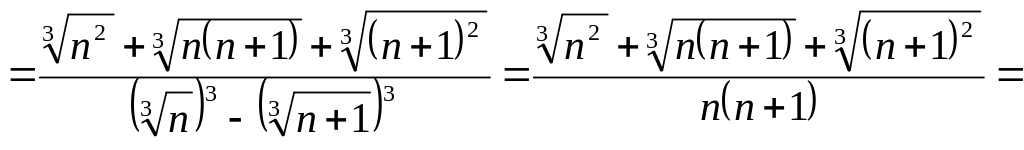