
I уровень
1.1. Найдите функцию, обратную данной, если она существует:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
1.2. Докажите, что пары функций являются взаимно-обратными:
1)![]() и
и
![]() если
если
![]()
2)![]() и
и
![]()
3)![]() и
и
![]()
4)![]() и
и
![]() если
если
![]()
1.3. Постройте график функции и ей обратной (если она существует) в одной системе координат:
1)
если
![]() 2)
2)
![]()
3)![]() 4)
4)![]() если
если
![]()
1.4. Найдите точку (точки), принадлежащую кривой для заданного значения х0:
1)
![]()
![]()
2)
![]()
![]()
3)
![]()
![]()
1.5. Запишите функцию (функции) в явном виде:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
1.6. Найдите соответствующие точки
кривой, заданной параметрически, если
указаны значения параметра t:
![]()
![]()
![]()
![]()
![]()
1)
![]() 2)
2)
![]() 3)
3)
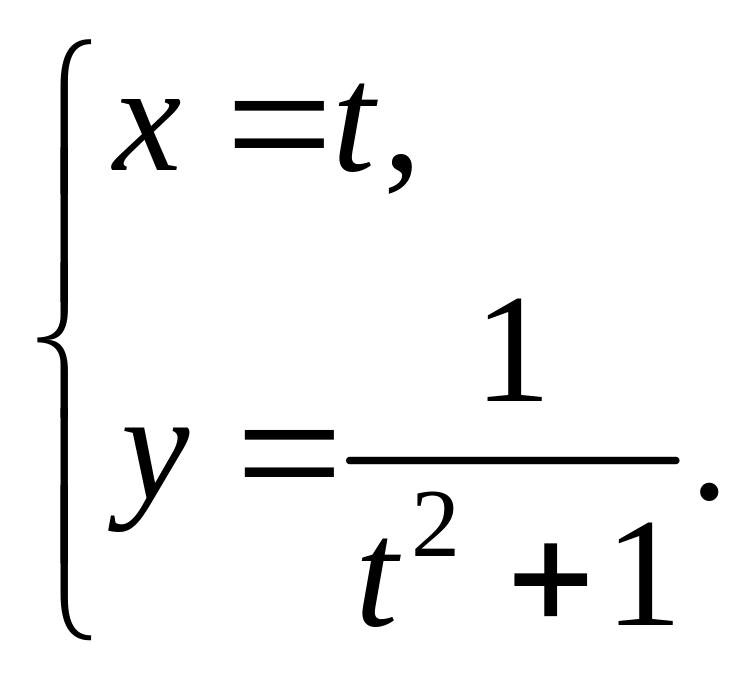
II уровень
2.1. Найдите функцию, обратную данной, и постройте их графики в одной системе координат:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
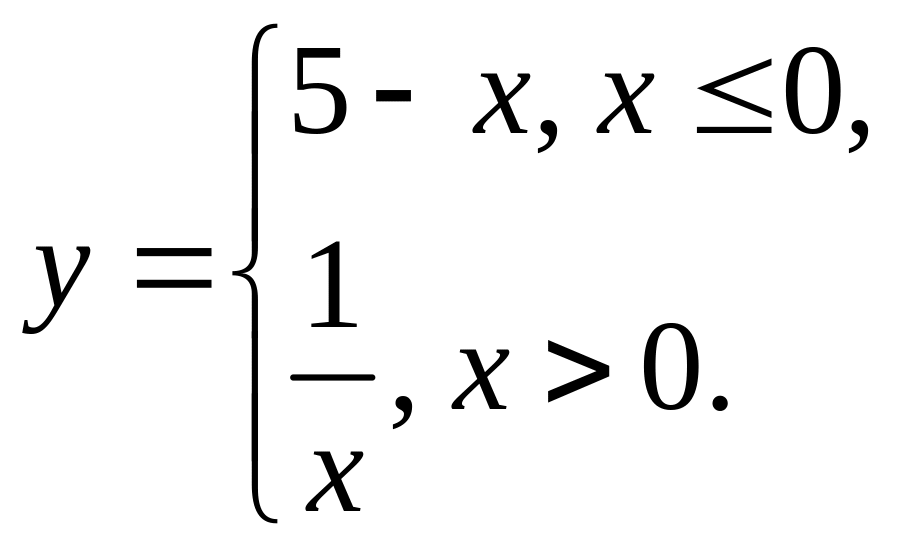
2.2. Определите, обратима ли функция
![]()
2.3. Найдите точки пересечения графиков
функции
![]() где
где
![]() и обратной ей функции.
и обратной ей функции.
2.4. Пусть графиком функции является полуокружность с центром О(0; 0) и радиусом, равным 5, расположенная в нижней координатной полуплоскости. Определите, существует ли функция, обратная данной.
2.5. Пусть задана функция
![]()
Найдите промежутки, на которых данная функция обратима.
2.6. Выразите явно у через х из уравнения и постройте данную линию:
1)
![]()
2)
![]() если
если
![]()
3)
![]() если
если
![]()
4)
![]() если
если
![]()
2.7. Постройте линию, заданную параметрически уравнениями:
1)
![]()
![]() 2)
2)
![]()
![]()
3)
![]()
![]() 4)
4)
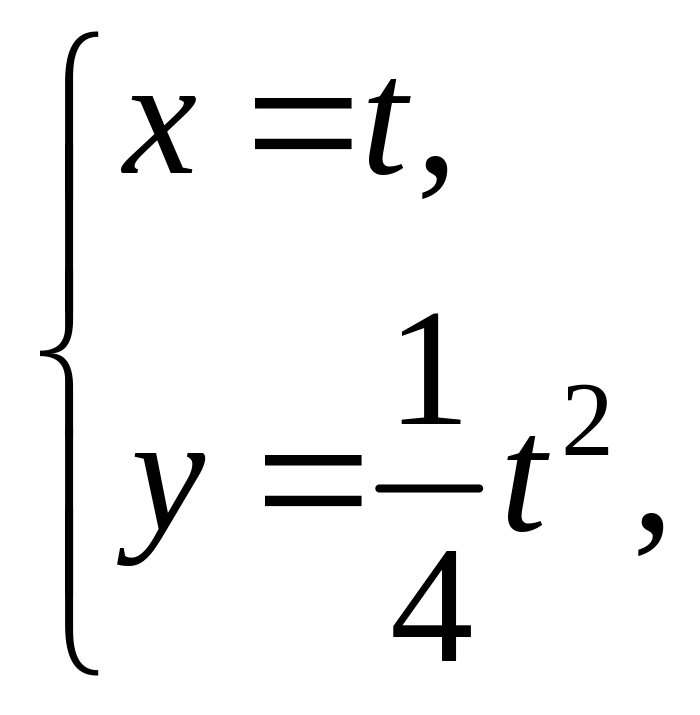
![]()
III уровень
3.1. Найдите функцию, обратную данной, и постройте их графики в одной системе координат:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]()
![]() 6)
6)
![]()
3.2. Докажите, что функция
![]() обратна сама себе.
обратна сама себе.
3.3. Найдите
![]() если функция
если функция
![]() обратна функции
обратна функции
![]()
4.3. Преобразования графиков
Приведем графики некоторых функций:
1)
|
2)
парабола (рис. 4.8); |

Рис. 4.7 Рис. 4.8
3)
|
4)
(рис. 4.10); |
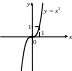
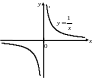
Рис. 4.9 Рис. 4.10
5)
![]() – график квадратного корня (рис. 4.11).
– график квадратного корня (рис. 4.11).
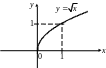
Рис. 4.11
Правила преобразования графиков:
Пусть дана функция
![]()
1. Для построения графика функции
![]() исходный график функции
симметрично отображаем относительно
оси Ох (рис. 4.12).
исходный график функции
симметрично отображаем относительно
оси Ох (рис. 4.12).
2. Для функции
![]() заданный график симметрично отображаем
относительно оси Оу (рис. 4.13).
заданный график симметрично отображаем
относительно оси Оу (рис. 4.13).

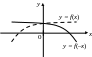
Рис. 4.12 Рис. 4.13
3. Для функции
![]() этот график получается параллельным
переносом графика функции
на
этот график получается параллельным
переносом графика функции
на
![]() масштабных единиц вдоль оси Оу
вверх, если
масштабных единиц вдоль оси Оу
вверх, если
![]() и вниз, если
и вниз, если
![]() (рис. 4.14).
(рис. 4.14).
4. Для функции
![]() этот график получается параллельным
переносом графика функции
на
этот график получается параллельным
переносом графика функции
на
![]() масштабных единиц вдоль оси Ох
вправо, если
масштабных единиц вдоль оси Ох
вправо, если
![]() и влево, если
и влево, если
![]() (рис. 4.15).
(рис. 4.15).
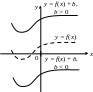
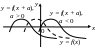
Рис. 4.14 Рис. 4.15
5. Для функции
![]() где
где
![]() график функции
«растянут» в k раз
вдоль оси Оу (от оси Ох), если
график функции
«растянут» в k раз
вдоль оси Оу (от оси Ох), если
![]() «сжат» в
«сжат» в
![]() раз вдоль оси Оу
(к оси Ох),
если
раз вдоль оси Оу
(к оси Ох),
если
![]() (рис. 4.16).
(рис. 4.16).
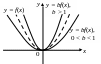
Рис. 4.16
6. Для функции
![]() где
где
![]() график
«растянут» вдоль оси Ох (от оси Оу)
в
график
«растянут» вдоль оси Ох (от оси Оу)
в
![]() раз при
раз при
![]() «сжат» вдоль Ох (к оси Оу) в
m раз, при
«сжат» вдоль Ох (к оси Оу) в
m раз, при
![]() (рис. 4.17).
(рис. 4.17).
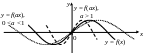
Рис. 4.17
7. Для функции
![]() сохраняется та часть графика функции
сохраняется та часть графика функции
![]() которая находится над осью Ох и на
оси Ох, а та часть, которая находится
под осью Ох, отображается симметрично
оси Ох в верхнюю полуплоскость (рис.
4.18).
которая находится над осью Ох и на
оси Ох, а та часть, которая находится
под осью Ох, отображается симметрично
оси Ох в верхнюю полуплоскость (рис.
4.18).
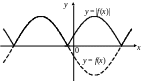
Рис. 4.18
8. Для функции
![]() часть графика функции
соответствующая отрицательному значению
х, отбрасывается, а неотрицательному
– сохраняется и дополняется симметричной
ей относительно оси Оу частью (рис.
4.19).
часть графика функции
соответствующая отрицательному значению
х, отбрасывается, а неотрицательному
– сохраняется и дополняется симметричной
ей относительно оси Оу частью (рис.
4.19).
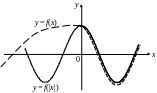
Рис. 4.19
Пример 1.
Построить график функции
![]()
Решение. Преобразуем заданную функцию:
![]()
![]()
Получили
![]()
Для построения графика полученной функции используем следующие преобразования:
строим график функции
график функции
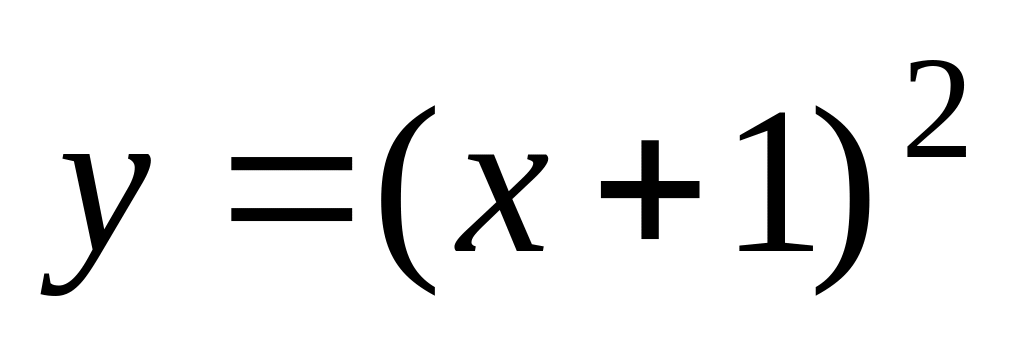 получаем из графика функции
путем движения его на единицу влево по
оси Ох;
получаем из графика функции
путем движения его на единицу влево по
оси Ох;график функции
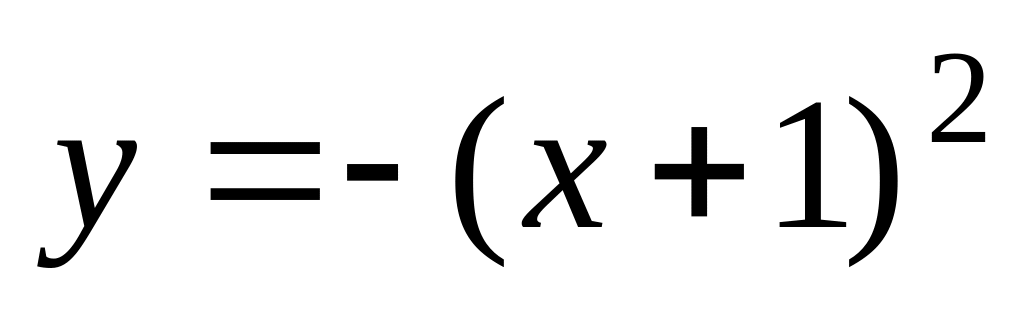 получаем из предыдущего симметричным
отображением относительно оси Ох;
получаем из предыдущего симметричным
отображением относительно оси Ох;график заданной функции получаем из графика функции параллельным переносом на две единицы вниз по оси Оу (рис. 4.20).
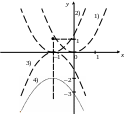
Рис. 4.20
Пример 2.
Построить график функции
![]()
Решение. Вначале преобразуем формулу, задающую функцию:
![]()
Шаги построения (рис. 4.21):
1)
![]()
2)
![]() – отображение симметрично оси Оу
в левую полуплоскость;
– отображение симметрично оси Оу
в левую полуплоскость;
3)
![]() – смещение вдоль оси Ох
вправо на две единицы;
– смещение вдоль оси Ох
вправо на две единицы;
4)
![]() – увеличение коэффициента роста в два
раза.
– увеличение коэффициента роста в два
раза.
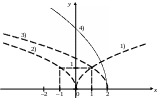
Рис. 4.21
Пример 3. Построить
график функции
![]() и найти наибольшее значение функции,
если
и найти наибольшее значение функции,
если
![]()
Решение.
![]()
Преобразуем функцию
![]()
Данный график
может быть получен из графика функции
![]() следующими преобразованиями (рис. 4.22):
следующими преобразованиями (рис. 4.22):
1)
![]() – смещение вдоль оси Ох
на единицу влево;
– смещение вдоль оси Ох
на единицу влево;
2)
![]() – смещение вдоль оси Оу
вверх на единицу;
– смещение вдоль оси Оу
вверх на единицу;
3)
![]() – отображение той части графика у3,
которая расположена ниже оси Ох,
в верхнюю полуплоскость (рис. 4.22). Заметим,
что такие же преобразования необходимо
применить к асимптотам функции
– отображение той части графика у3,
которая расположена ниже оси Ох,
в верхнюю полуплоскость (рис. 4.22). Заметим,
что такие же преобразования необходимо
применить к асимптотам функции
![]() (вертикальной) и
(вертикальной) и
![]() (горизонтальной).
(горизонтальной).
Анализ графика
показывает, что наибольшее значение на
![]() функция достигает в точке
функция достигает в точке
![]() Вычисляем его:
Вычисляем его:
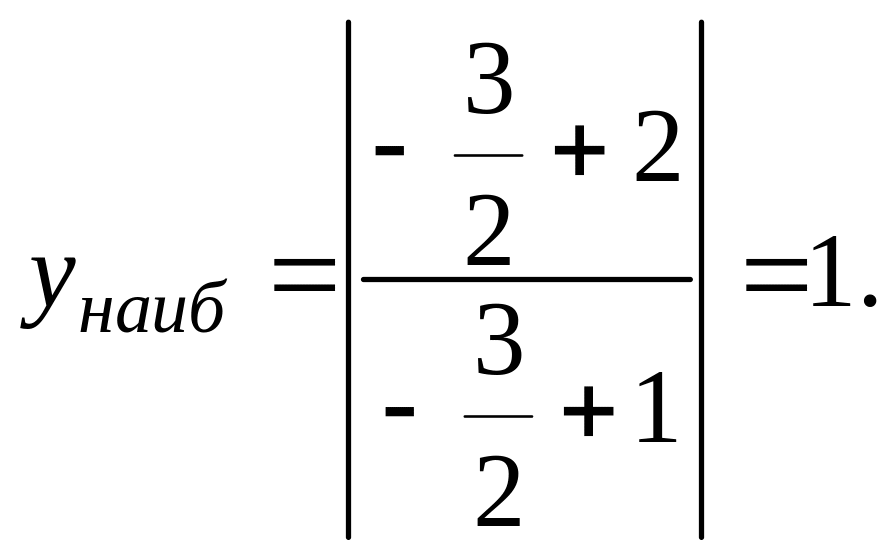

Рис. 4.22
Пример 4. Определить, при каком значении а уравнение имеет ровно 3 решения:
![]()
Решение. Решим задачу графически.
Построим графики
функций
![]() и
и
![]() и исследуем, при каком значении а
они имеют ровно 3 общие точки.
и исследуем, при каком значении а
они имеют ровно 3 общие точки.
Строим график
функции
![]()
Поскольку
![]() то
то
![]() – это парабола,
вершина которой смещена в точку
– это парабола,
вершина которой смещена в точку
![]()
Для построения графика функции сохраняем ту часть графика параболы, которая находится над осью Ох и на оси Ох, а ту часть графика, которая находится под осью Ох, отображаем симметрично оси Ох в верхнюю полуплоскость.
![]() – прямая, параллельная
оси Ох
(рис. 4.23).
– прямая, параллельная
оси Ох
(рис. 4.23).
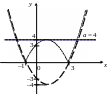
Рис. 4.23
По построению
видно, что ровно 3 решения будет тогда
и только тогда, когда
![]()
Задания
I уровень
1.1. Постройте график функции:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
II уровень
2.1. Постройте график функции:
1)
![]()
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
2.2. Постройте график функции:
1)
 2)
2)
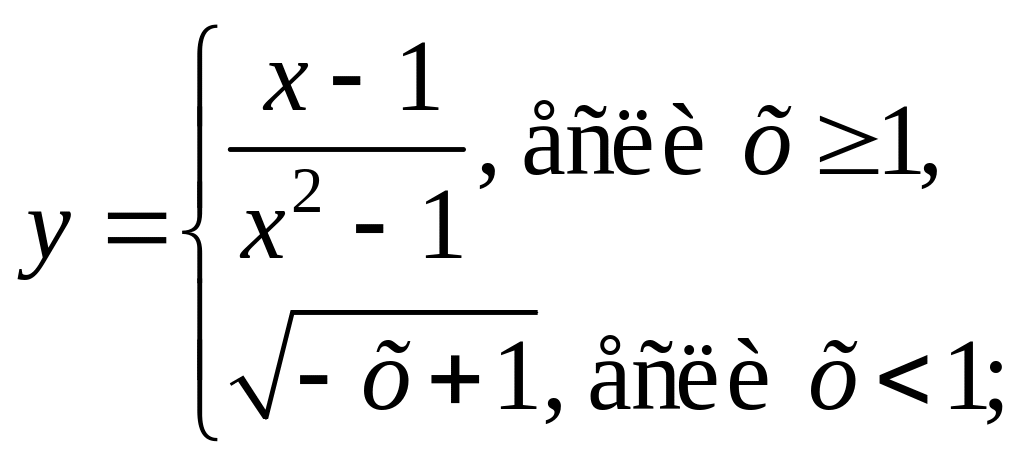
3)
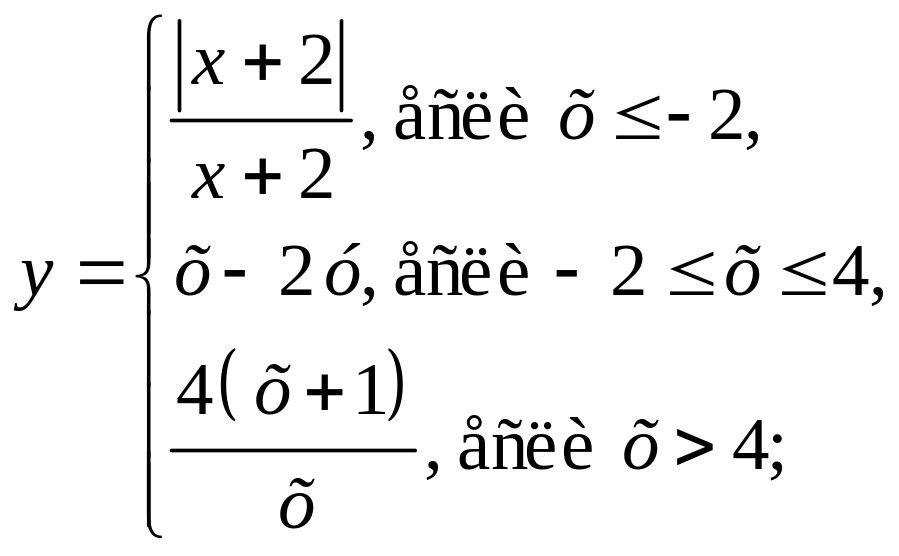 4)
4)
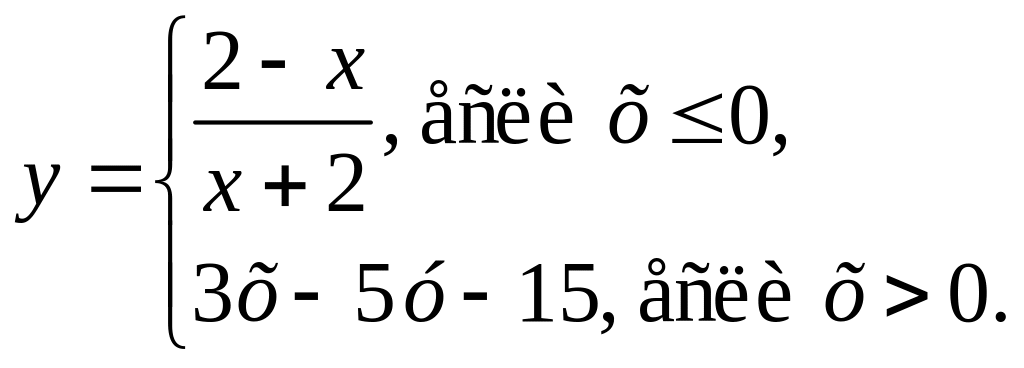
2.3. Определите, при каком значении a система имеет ровно одно решение:
1)
![]() 2)
2)

2.4. Определите, при каких значениях a система имеет ровно два решения:
1)
![]() 2)
2)
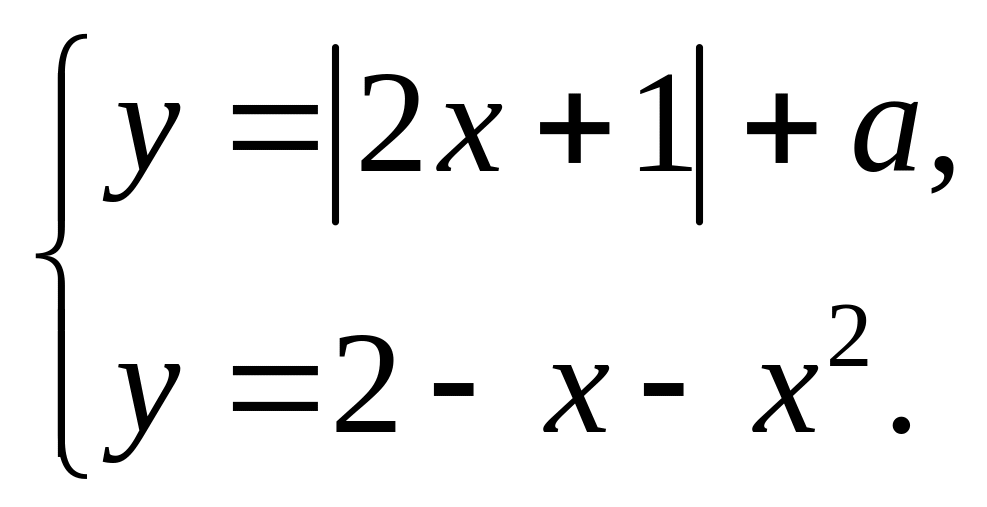
В ответе запишите сумму полученных значений.
III уровень
3.1. Постройте график функции:
1)
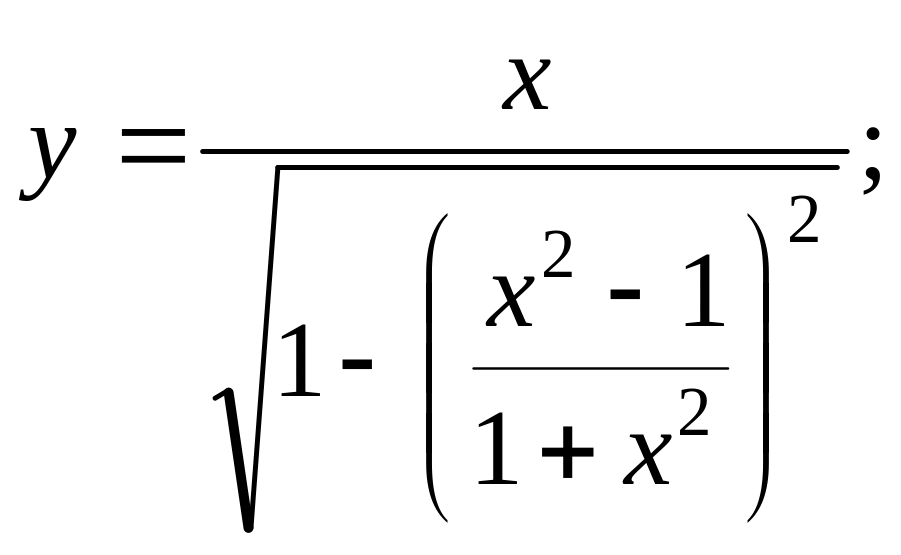 2)
2)
![]()
3)
![]() 4)
4)
![]()
3.2. Определите, при каком значении
b система
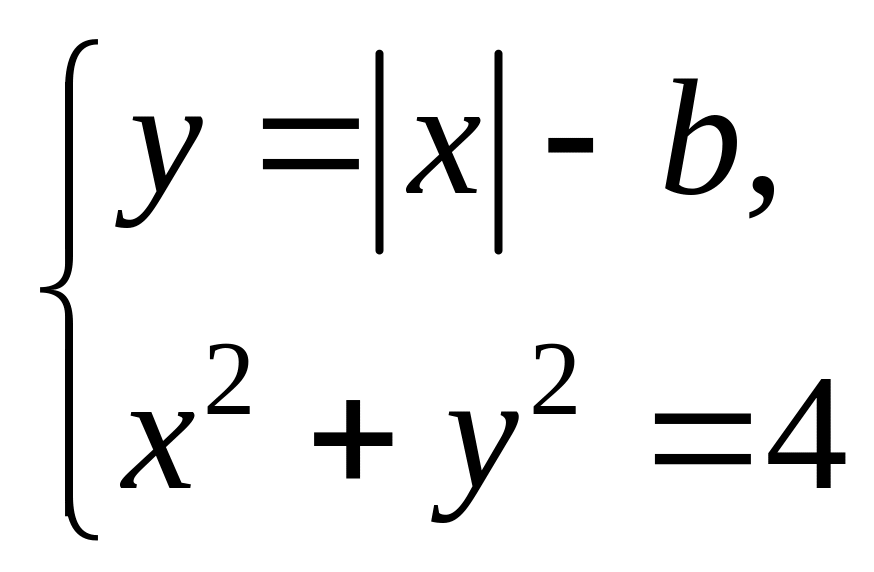 имеет:
имеет:
1) одно единственное решение;
2) ровно три решения;
3) более трех решений;
4) не имеет решений.
3.3. Найдите наибольшее и наименьшее
значения функции
![]() если
если
![]() Выполните построение.
Выполните построение.
4.4. Неравенства с двумя переменными и их системы
Неравенством с двумя переменными х и у называется неравенство вида
![]() (или знак
(или знак
![]() ),
),
где
![]() – некоторое выражение с данными
переменными.
– некоторое выражение с данными
переменными.
Решением неравенства с двумя
переменными называют упорядоченную
пару чисел
![]() при которой это неравенство обращается
в верное числовое неравенство.
при которой это неравенство обращается
в верное числовое неравенство.
Решить неравенство – значит найти множество всех его решений. Решением неравенства с двумя переменными является некоторое множество точек координатной плоскости.
Основным методом решений данных неравенств является графический. Он заключается в том, что строят линии границ (если неравенство строгое, линии строят пунктиром). Уравнение границы получают, если в заданном неравенстве заменяют знак неравенства на знак равенства. Все линии в совокупности разбивают координатную плоскость на части. Искомое множество точек, которое соответствует заданному неравенству или системе неравенств, можно определить, если взять контрольную точку внутри каждой области.
Системы, содержащие неравенства с двумя переменными, вида
![]()
называются системами неравенств с двумя переменными. Решением данных систем является пересечение решений всех неравенств, входящих в систему.
Совокупность неравенств с двумя переменными имеет вид
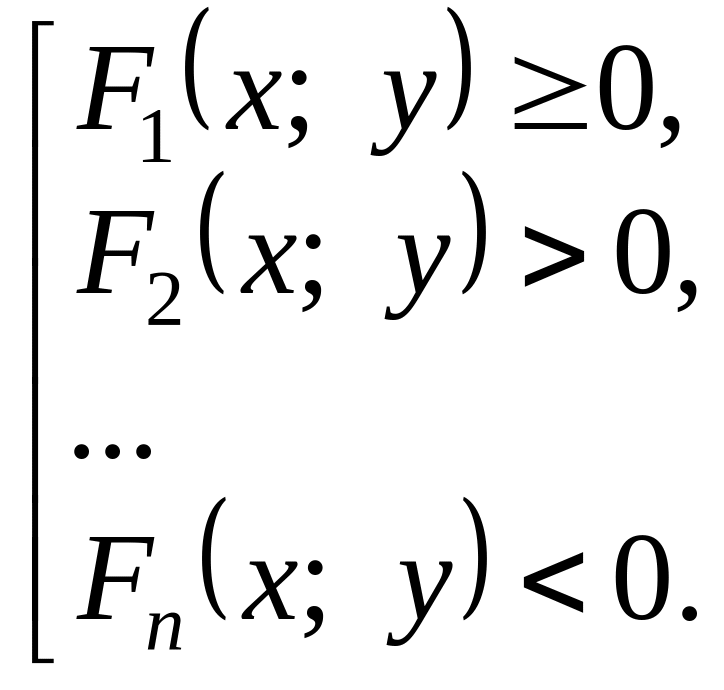
Решением совокупности является объединение всех решений неравенств.
Пример 1.
Решить
систему
![]()
Решение. Построим в системе Оху соответствующие линии (рис. 4.24):
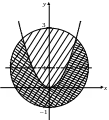
Рис. 4.24
Уравнение
![]() задает окружность с центром в точке
О(0;
1) и R
= 2.
задает окружность с центром в точке
О(0;
1) и R
= 2.
Уравнение
![]() определяет параболу с вершиной в точке
О(0;
0).
определяет параболу с вершиной в точке
О(0;
0).
Найдем решения каждого из неравенств, входящих в систему. Первому неравенству соответствует область внутри окружности и сама окружность (в справедливости этого убеждаемся, если подставим в неравенство координаты любой точки из этой области). Второму неравенству соответствует область, расположенная под параболой.
Решение системы – пересечение двух указанных областей (на рис. 4.24 показано наложением двух штриховок).
Задания
