5. Комплексные числа.
5.1 Записать комплексное число
в тригонометрической и показательной
формах
Решение.
так как абсцисса отрицательна, а ордината положительна, то точка лежит во второй четверти.
,
,
,
т.е.
.
Поэтому
.
5.2. Записать комплексное число
в тригонометрической и показательной
формах
Решение.
,
,
,
т.е.
и
.
5.3. Выполнить следующие операции над комплексными числами.
Решение.
1)
2)
3)
5.4. Найти
.
Решение.
Запишем сначала число
в тригонометрической форме:
;
,
.
По формуле Муавра имеем
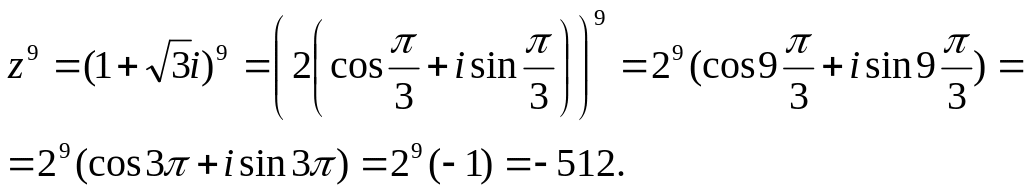
5.5 Найти частное
.
Решение:
.
5.6. Найти
.
Решение. Запишем подкоренное
выражение в тригонометрической форме
.
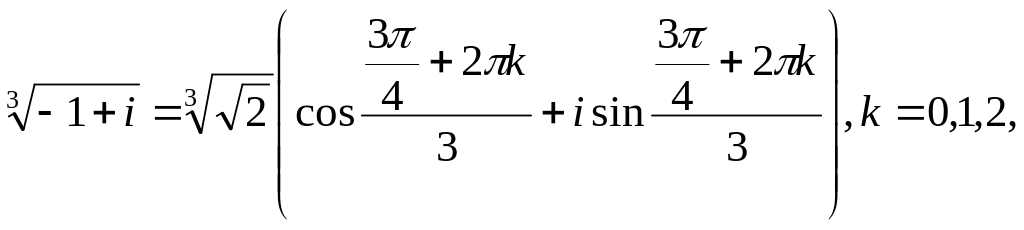
Откуда получаем три значения корня
при
,
при
,
при
.
На комплексной плоскости найденные
значения корня представляют равноотстоящие
друг от друга точки
,
,
,
расположенные на окружности радиуса
.
5.7. Изобразить на рисунке множество
точек
комплексной плоскости, удовлетворяющих
условию:
Решение:
1) Запишем
в алгебраической форме
,
тогда
.
Найдем
.
Тогда
(возведем в квадрат),
.
- окружность с центром
и радиусом 2.
Н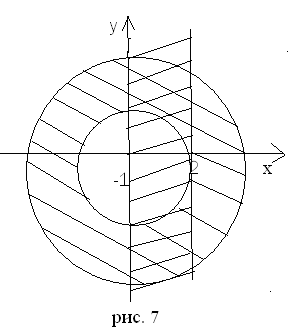
еравенство
задает множество точек, лежащих за
пределами окружности.
- окружность с центром
и радиусом 4. Неравенство
задает множество точек, лежащих внутри
окружности.
2)
,
т.е. получаем неравенства
.
Изобразим полученные множества точек.
Решением является пересечение заштрихованных областей.
5.8. Найти все корни уравнения
.
Решение. .
.
.
5.9. Доказать, что если число
является чисто мнимым, то
.
Решение. По условию
,
где
- действительное число. Тогда
,
,
5.10. Решите уравнение
.
Решение:
,
.
Тогда получим уравнение
Из определения равенства комплексных чисел следует
,
,
,
.
Следовательно,
.