Поверхности 2 порядка.
3.17. Определить вид и параметры поверхности второго порядка, заданной уравнением
Решение. Преобразуем это уравнение, выделив в левой части полные квадраты:
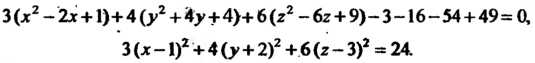
Введем новые координаты по формулам:
(I)
Тогда уравнение примет вид
Полученное уравнение определяет
эллипсоид, для которого
Центр
эллипсоида находится в точке
В
новой системе
Координат центром является точка с
координатами
Из
этих равенств и формул (I) находим
Т.
е. координаты точки
3.18. Определить вид и параметры поверхности
Решение. Преобразуем это уравнение:
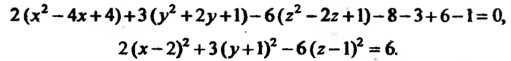
Переходя к новым координатам по
формулам
Получаем
Или
Это уравнение определяет однополостный
гиперболоид, для которого 
С
центром в точке
3.19. Доказать, что уравнение
Определяет
гиперболический параболоид.
Решение. Введем новые координаты
по формулам
Тогда Уравнение примет вид
Полученное уравнение является уравнением
вида x2/a2-y2/b2=2z,
для которого
,
;
оно определяет гиперболический
параболоид.
3.20 Приведите уравнение поверхности
к каноническому виду.
Решение. Квадратичная форма имеет вид
Выписываем ее матрицу
.
Находим ее собственные числа. Для этого запишем характеристическое уравнение
.
После вычисления определителя получим
.
Подбором находим один корень
.
Преобразуем уравнение, выделяя множитель
или
.
Находим два других корня характеристического
уравнения
и
.
Находим собственные векторы. Для
собственного числа
для координат собственного вектора
получим систему уравнений
Решая ее находим, что фундаментальная
система решений содержит только одно
решение, и в качестве собственного
вектора можно взять
.
Для собственного числа
находим собственный вектор
.
Для собственного числа
находим собственный вектор
.
Легко проверить, что
,
то есть собственные векторы попарно
ортогональны. Их длины равны соответственно
.
Поэтому векторы нового ортонормированного
базиса будут иметь координаты
,
,
Матрица перехода имеет вид
.
Старые координаты связаны с новыми
уравнением
,
то есть
,
Подставим эти выражения в исходное уравнение. Квадратичная форма примет вид, в котором произведения переменных будут отсутствовать, а коэффициентами при квадратах будут служить собственные числа
Приводим подобные члены
Выделим полные квадраты
Выполняем параллельный перенос осей координат
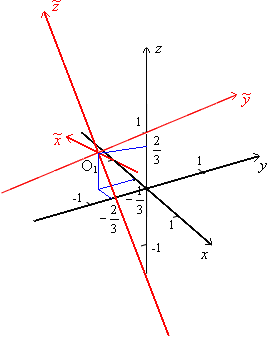
Новое начало системы координат О1 имеет координаты
В исходной системе координат точка О1 (подставляем в формулы замены) имеет координаты
Получили уравнение однополостного гиперболоида.
4 Абстрактная алгебра.
4.1. Бинарная операция
задана на множестве
.
Определить ее свойства, если
.
Решение.
Проверим коммутативность. Для этого
следует убедиться, что для всех
,
R
выполняется равенство
.
Поскольку
,
а
,
то условие коммутативности примет вид:
,
что равносильно тому, что
.
Ясно, что это равенство выполняется не всегда. Следовательно, заданная операция некоммутативна.
Проверим теперь ассоциативность
операции, то есть выясним, при каких x,
y, z
имеет место равенство
.
Точнее, нас интересует только один факт: при всех ли значениях переменных это равенство справедливо. Преобразуем выражения:
;
.
Очевидно, что полученные выражения не всегда дают равные значения. Приведем контрпример.
Пусть
,
,
.
Тогда:
;
.
Следовательно, ассоциативность не выполняется.
4.2 Задано отображение
на множестве
.
Является ли оно бинарной операцией,
если
?
Решение.
Пусть
.
Поскольку арифметические действия
умножения, сложения и вычитания однозначно
определены для любых действительных
чисел, то ясно, что
определено однозначно и
.
Покажем, что
.
Предположим, что
,
т.е.
.
Тогда, упростив, получаем
.
Получаем противоречие, так как
.
Полученное противоречие показывает,
что
.
Следовательно,
,
и правило * есть бинарная операция.
4.3. На множестве действительных
чисел определена бинарная операция
(*) следующим образом:
.
Найти корень уравнения
.
Решение.
Имеем:
,
,
.
4.4. Примеры операций над множествами.
Решение.
1) Пусть
Тогда
2) Пусть
Тогда
3) Пусть
Тогда
4) Пусть
Тогда
4.5 Найти образ и ядро оператора,
заданного матрицей A =
.
Решение.
Область значений оператора - образ-– это множество всех векторов
.
Ядро линейного оператора – это множество
всех векторов, которые А отображает в
нуль-вектор, т.е. решение
:
.
4.6. Найти матрицу и образ оператора А, действующего в R3 следующим образом:
.
Решение:
Матрица оператора имеет вид:
.
Образ оператора
