22

Тренировочные задачи и упражнения

Специальность ИВТ

Дисциплина алгебра и геометрия

1 семестр

2012-2013

Модуль 1

1 Линейная алгебра.

1. Даны матрицы А = 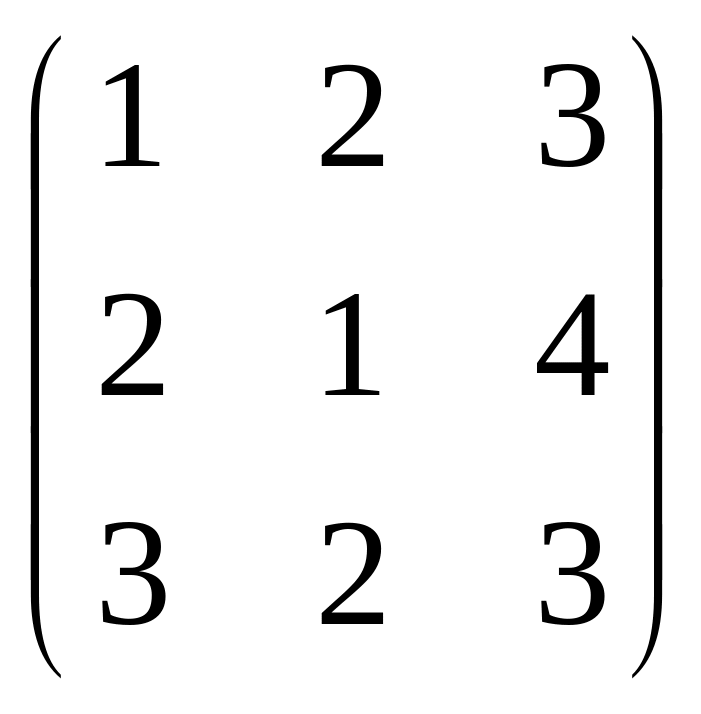; B = , найти 2А + В.

Решение. 2А = , 2А + В = .

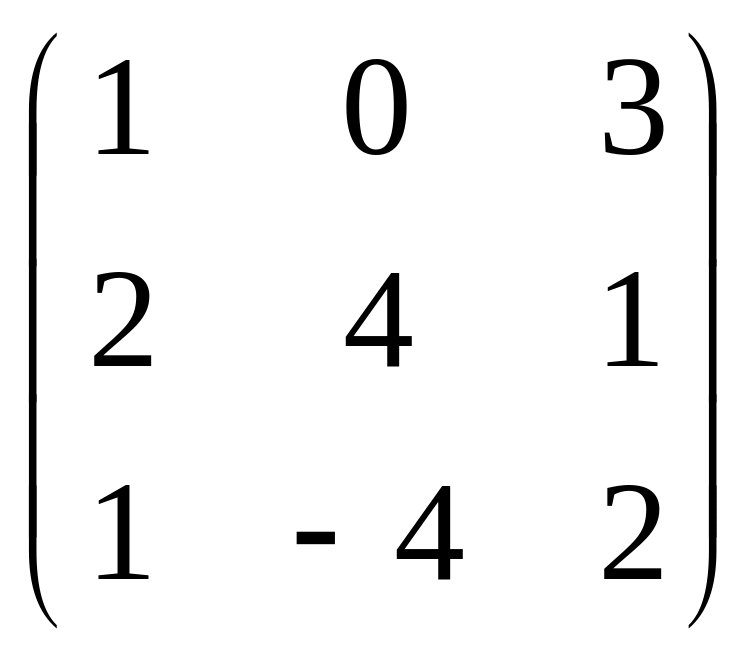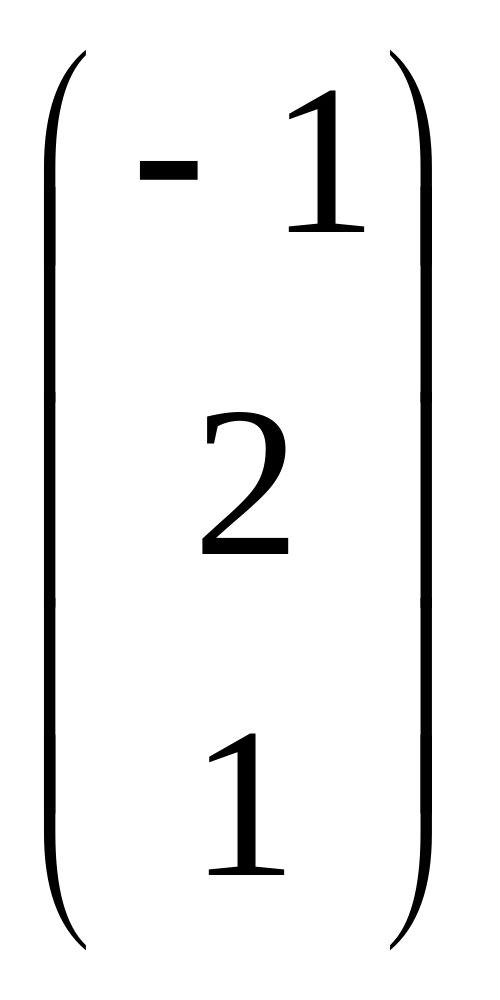2. Даны матрицы А = , В = , С = и число  = 2. Найти А^ТВ+С.

Решение. A^T = ;

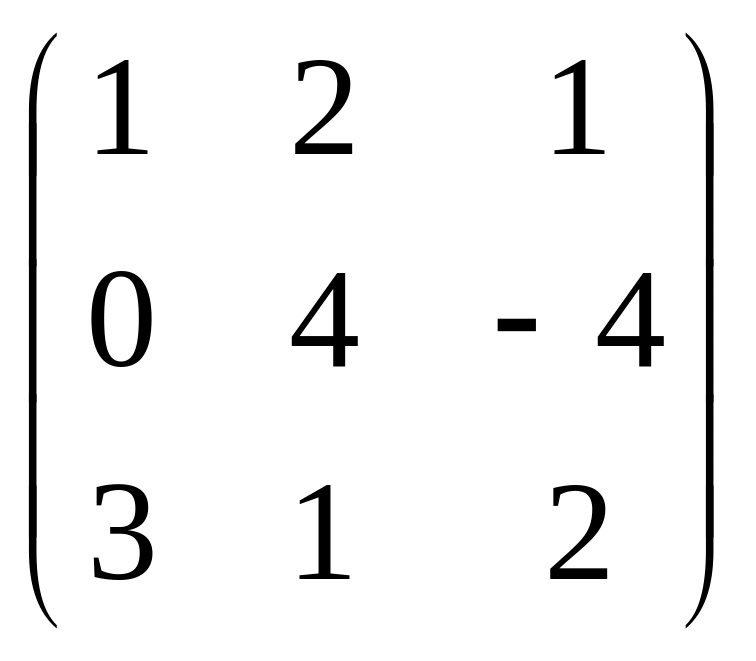A^TB = 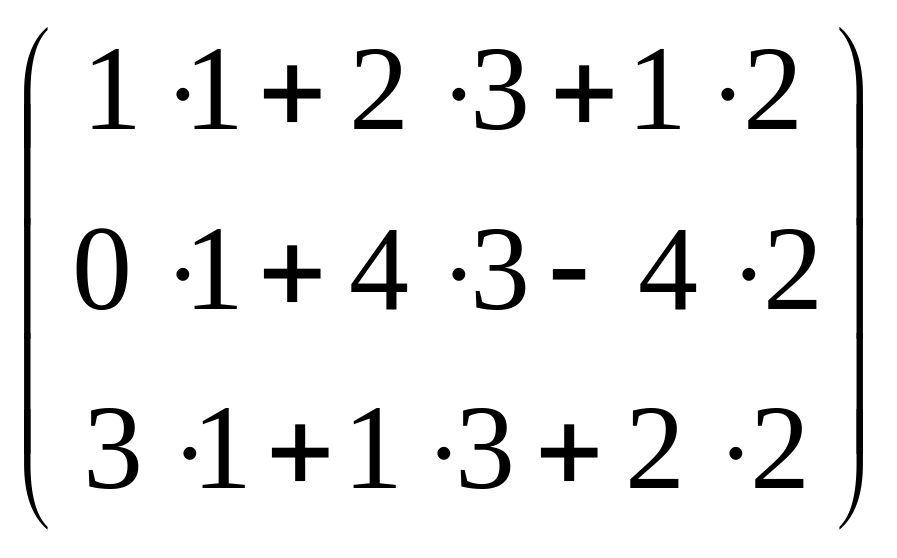 = = ; C = ;

А^ТВ+С = + = .

1.3 Вычислить определитель матрицы А =

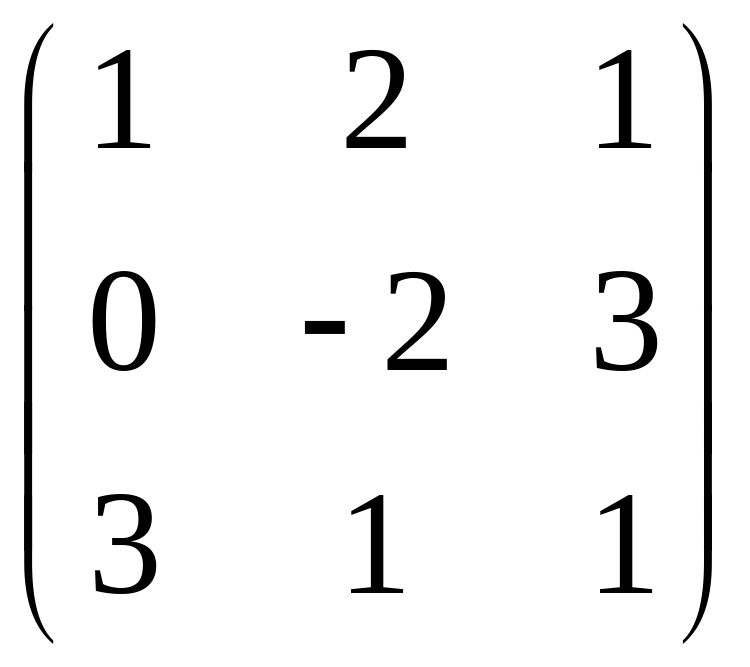
Решение:

= -5 + 18 + 6 = 19.(раскладывали по 1 строке.)

1.4. Найти значение матричного многочлена если .

Решение.

.

1.5. Определить ранг матрицы .

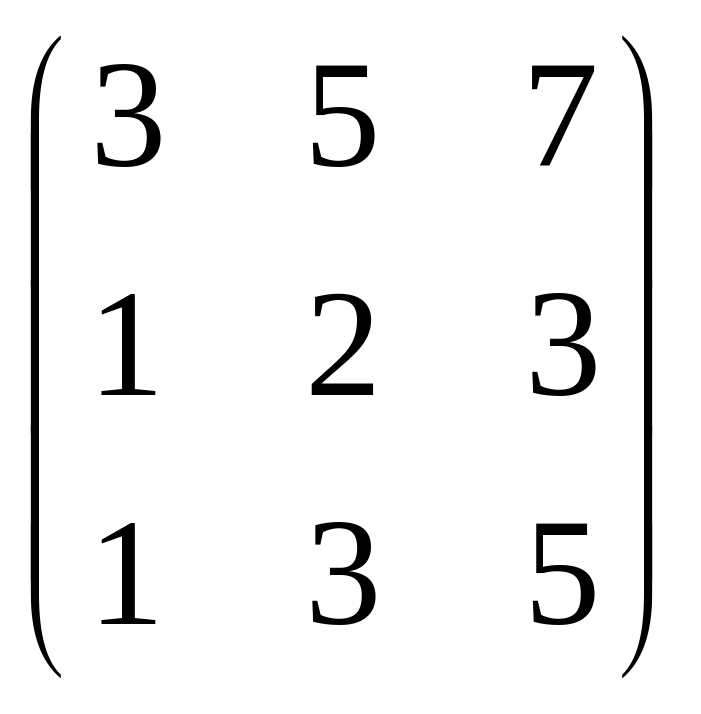Решение:

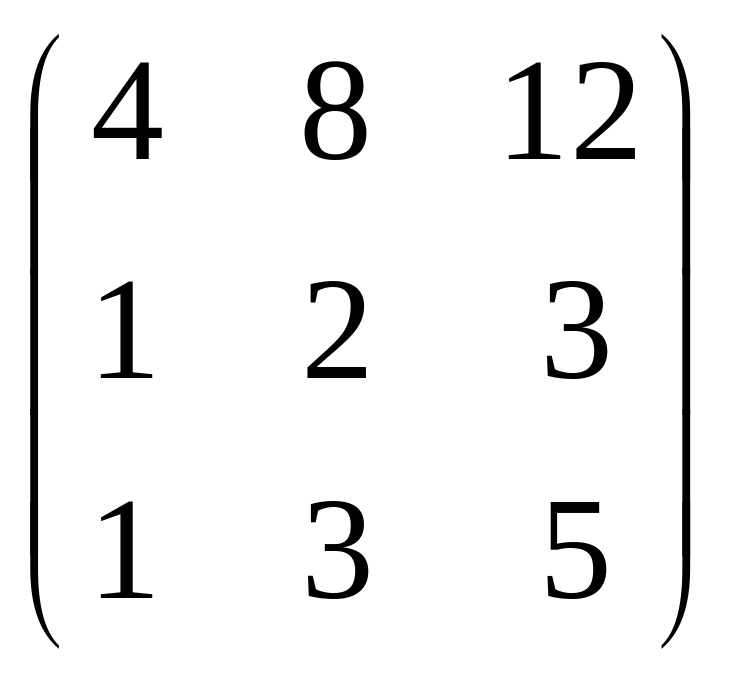
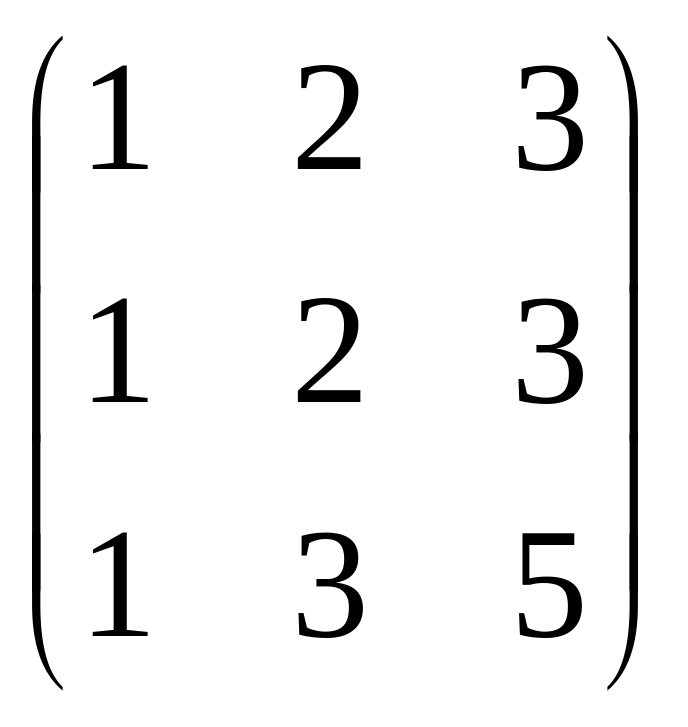1 стр.+3 стр ~  1стр.-2стр*4~ 1стр-2стр, нулевую отбрасываем~ , rang (А) = 2.

1.6 Определить след, норму матрицы .

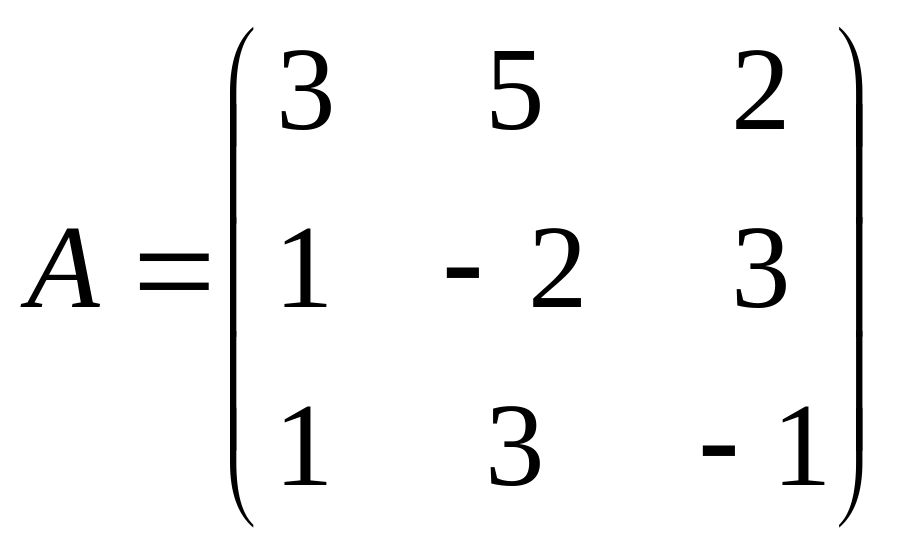Решение:

(сумма диагональных элементов)

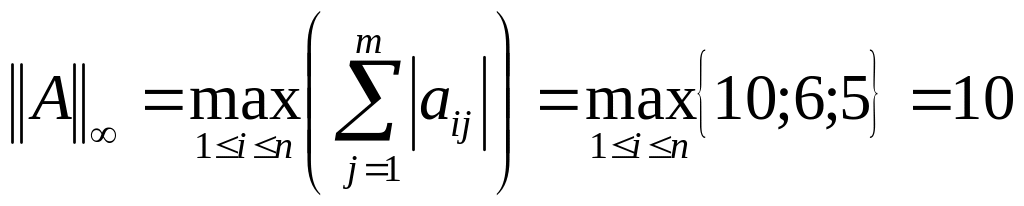
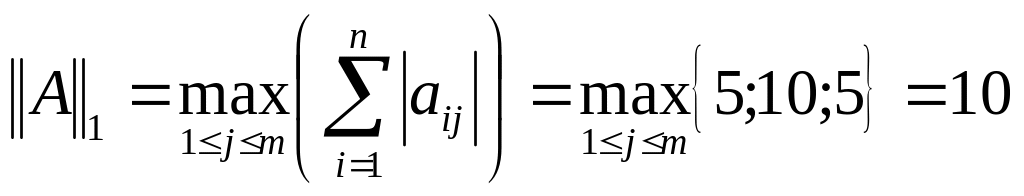
1.7 Решить систему уравнений матричным методом:

Решение:

Х = , B = , A =

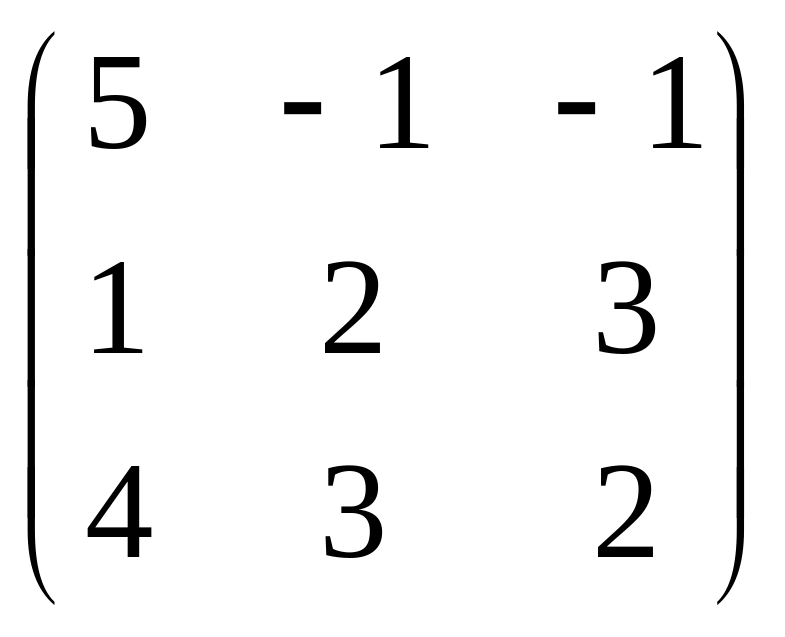
Найдем обратную матрицу А^-1.

 = det A = 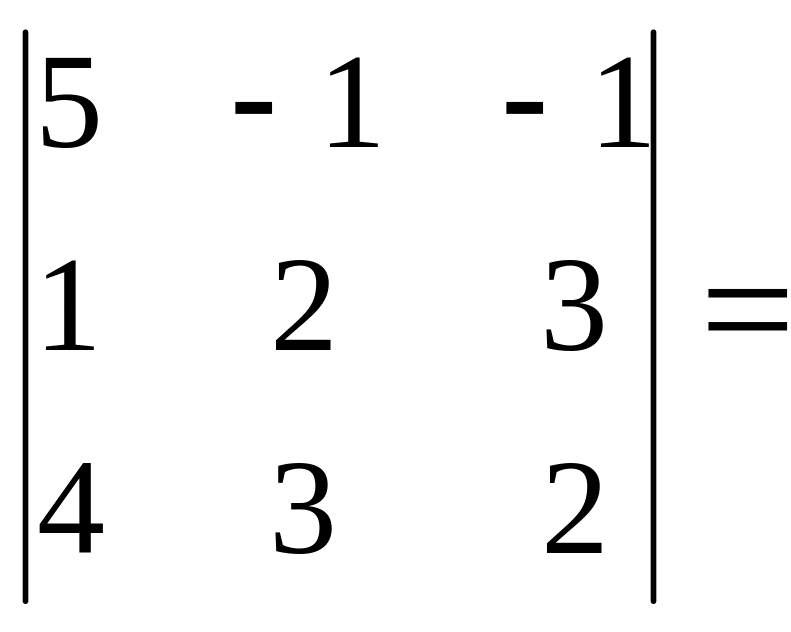5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.

А₁₁ = = -5; А₂₁ = - = -1; А₃₁ = = -1;

А₁₂ = - А₂₂ = А₃₂ = -

А₁₃ = А₂₃ = - А₃₃ =

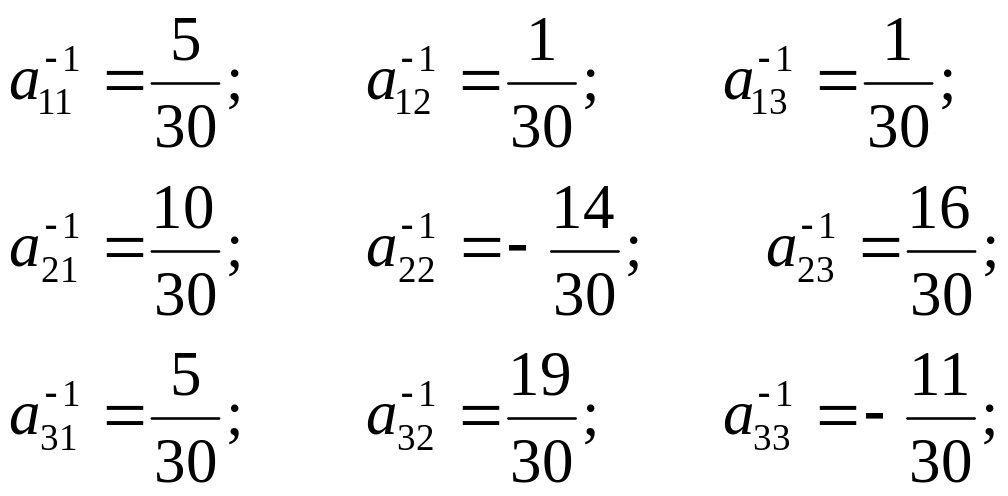A^-1 = ;

Сделаем проверку:

AA^-1 = 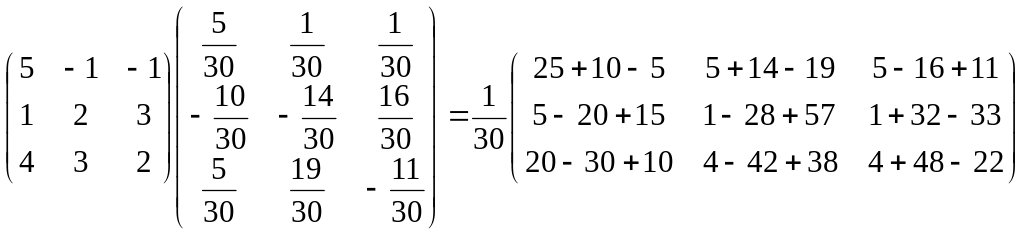=E.

Находим матрицу Х.

Х = = А^-1В =  = .

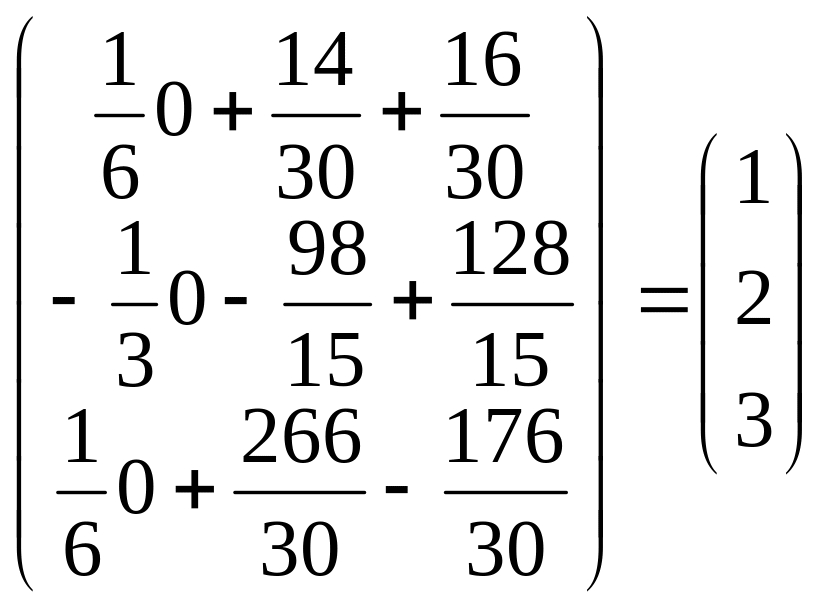Итого решения системы: x =1; y = 2; z = 3.

1.8. Найти число обусловленности матрицы A =

Решение.

Ранее нашли. A^-1 = ;

;

1.9 Найти решение системы уравнений Методом Крамера:

Решение:

 = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

x = 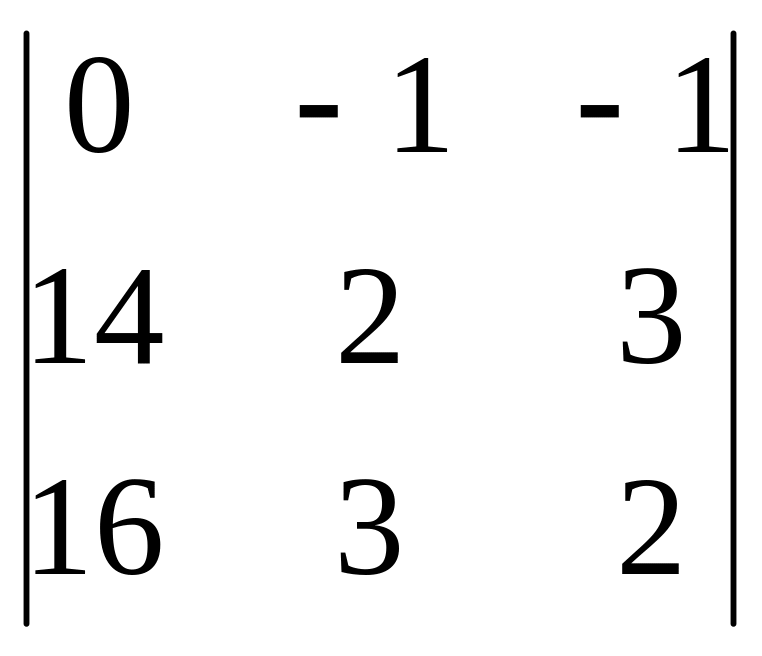= (28 – 48) – (42 – 32) = -20 – 10 = -30.

x = x/ = 1;

y = 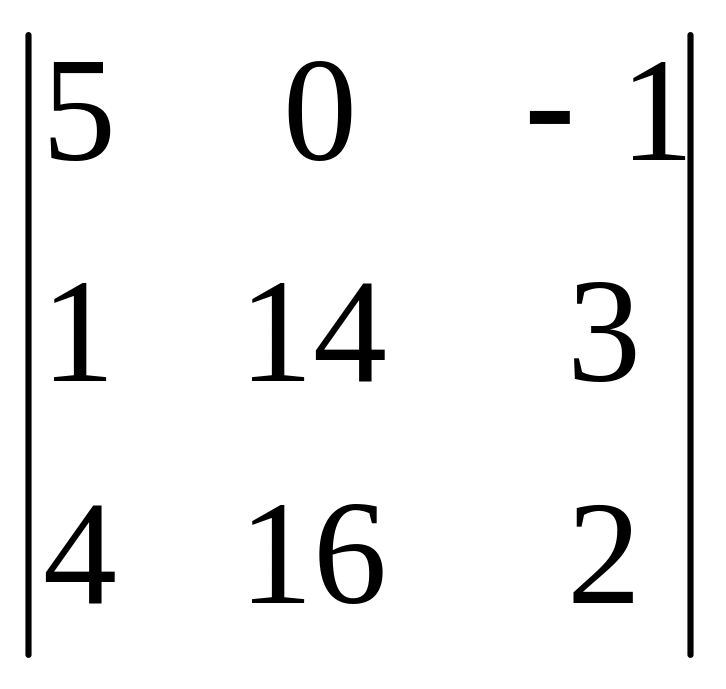= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

y = y/ = 2;

z = 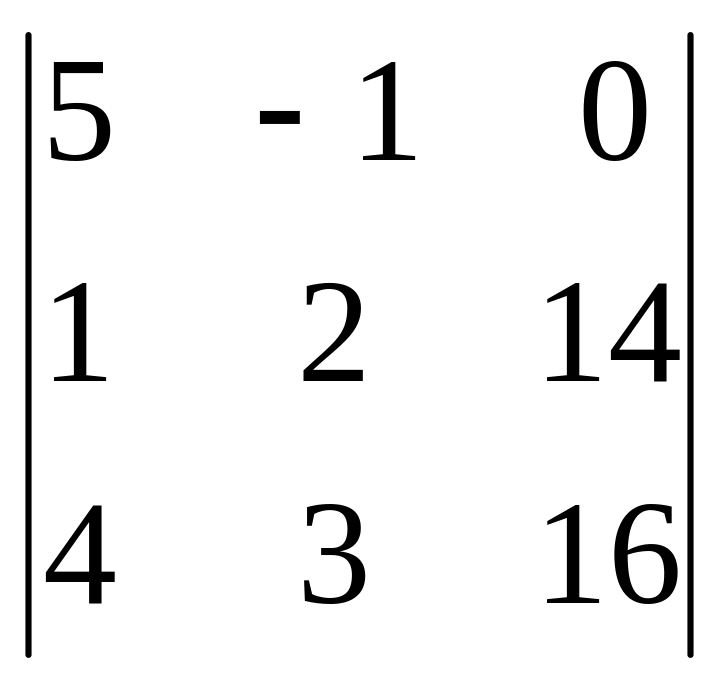= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.

z = z/ = 3.

1.10 Решить систему линейных уравнений методом Гаусса.

Решение:

Составим расширенную матрицу системы и преобразуем при помощи элементарных преобразований.

А* =

Таким образом, исходная система может быть представлена в виде:

, откуда получаем: x₃ = 2; x₂ = 5; x₁ = 1.

1.11. Найти собственные числа и собственные векторы оператора, заданного матрицей .

Решение.

Составим характеристическое уравнение имеет вид , получаем - собственные числа.

Решая для каждого собственного числа систему находим соответствующие им собственные векторы , .

1.12.. Найдите собственные числа и собственные векторы оператора, заданного матрицей .

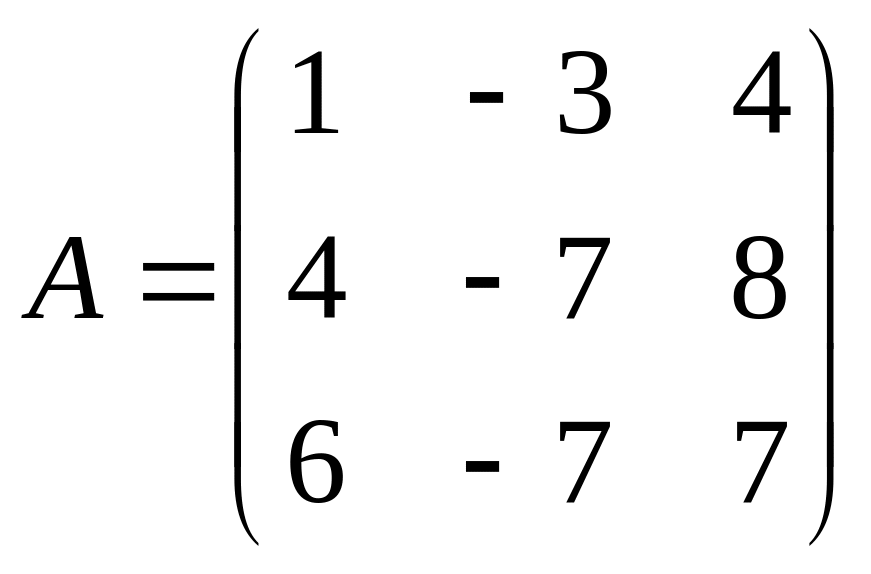Решение.

Составляем характеристическую матрицу :

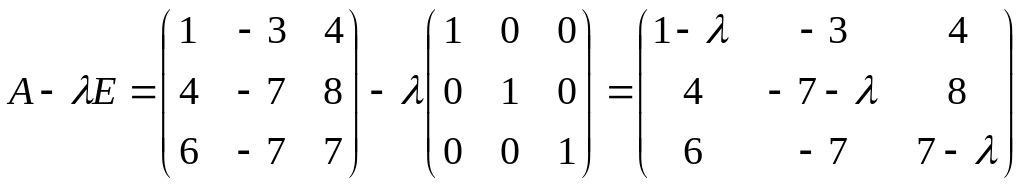
Решаем характеристическое уравнение .

Подбором находим один из корней -1.

Так как число -1 является корнем многочлена , то многочлен делится на разность , то есть , где - многочлен. Выделим в характеристическом многочлене множитель :

Находим корни трехчлена . Они равны -1 и 3. Таким образом,

- корень кратности 2 , - простой корень. Итак, собственные числа матрицы равны , . Найдем соответствующие им собственные векторы.

Пусть , тогда для собственного вектора X получаем матричное уравнение ,

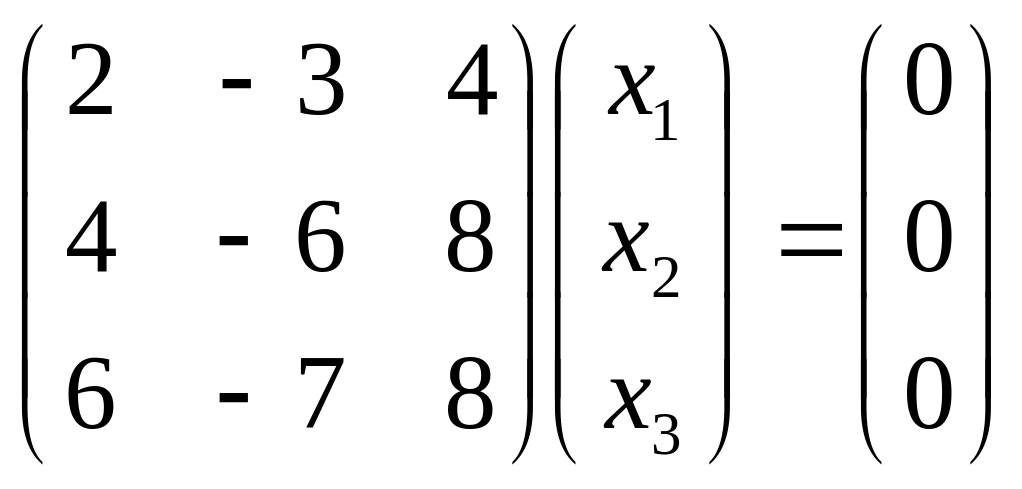что соответствует системе уравнений

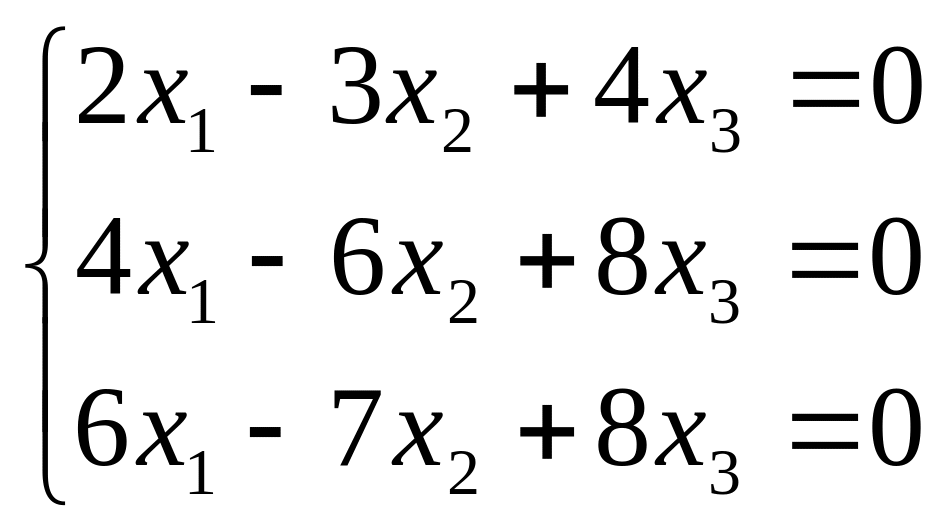
Решаем ее методом Гаусса. Выписываем расширенную матрицу системы

.

Первую строку, умноженную на числа -2 и -3 прибавляем соответственно ко второй и третьей строкам

.

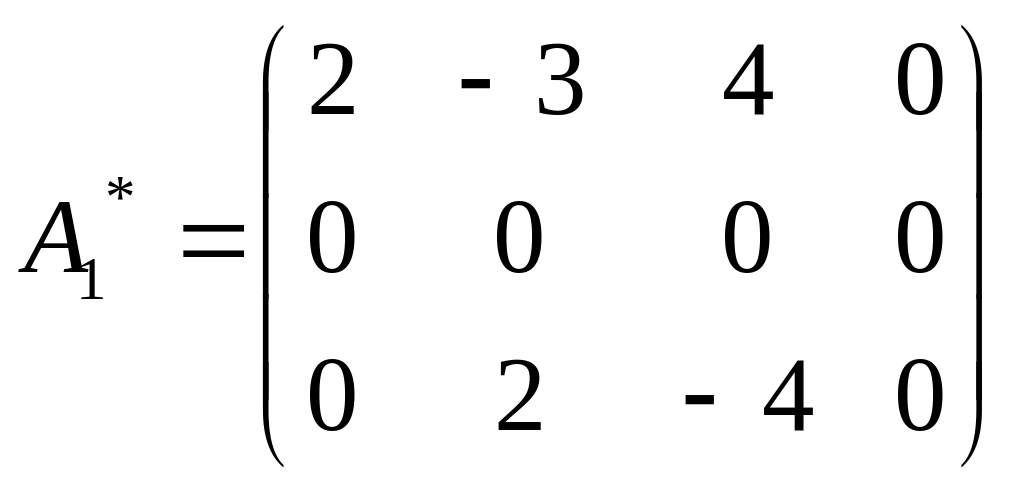Меняем местами вторую и третью строки

.

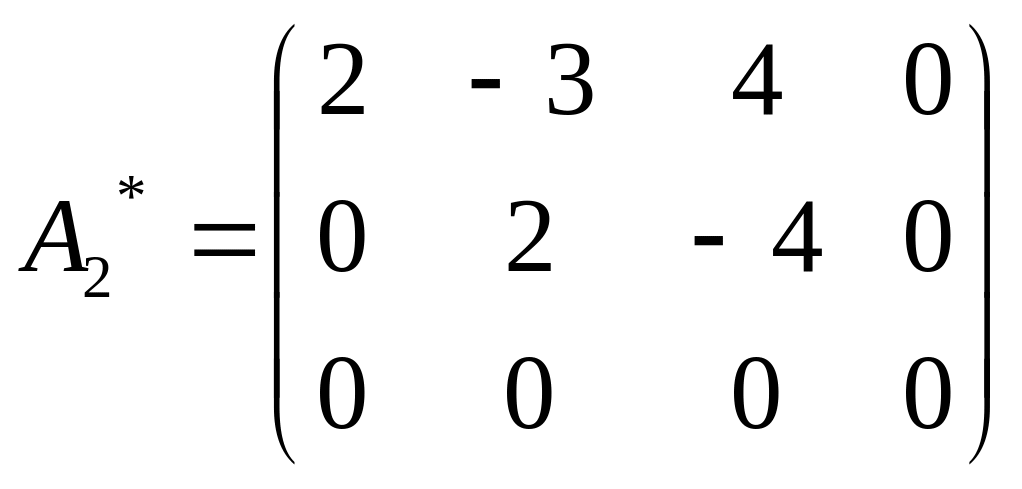Возвращаемся к системе уравнений .

Ранг матрицы равен 2. Число уравнений равно 2 (число линейно независимых строк), а число неизвестных 3. Поэтому фундаментальная система содержит только одно (3-2=1) решение. Переменные оставляем в левой части, а переменную переносим в правую часть

.

Полагаем , находим . Итак, собственному числу соответствует собственный вектор .

Пусть , тогда для собственного вектора получаем матричное уравнение

,

что соответствует системе уравнений

.

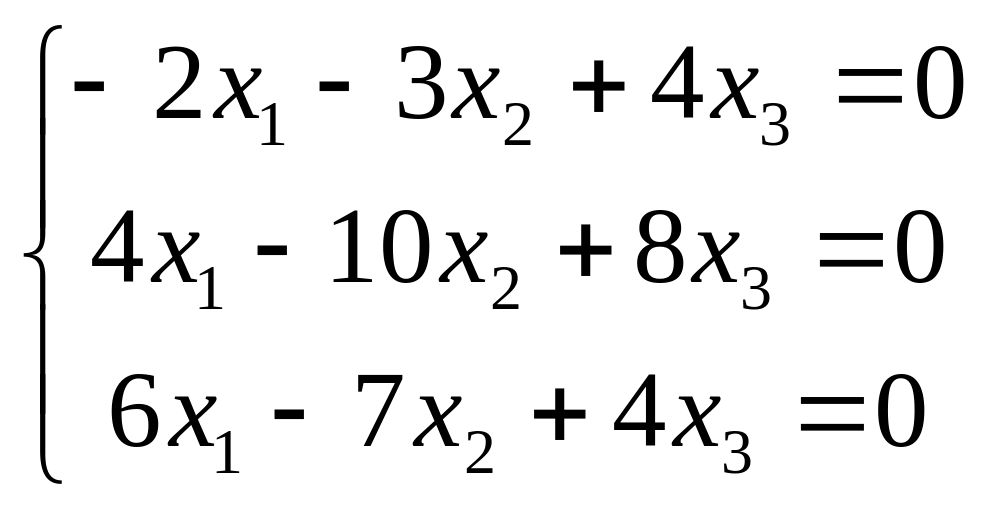Решаем ее методом Гаусса. Выписываем расширенную матрицу

Первую строку умножаем на числа 2 и 3 и прибавляем соответственно ко второй и третьей строкам

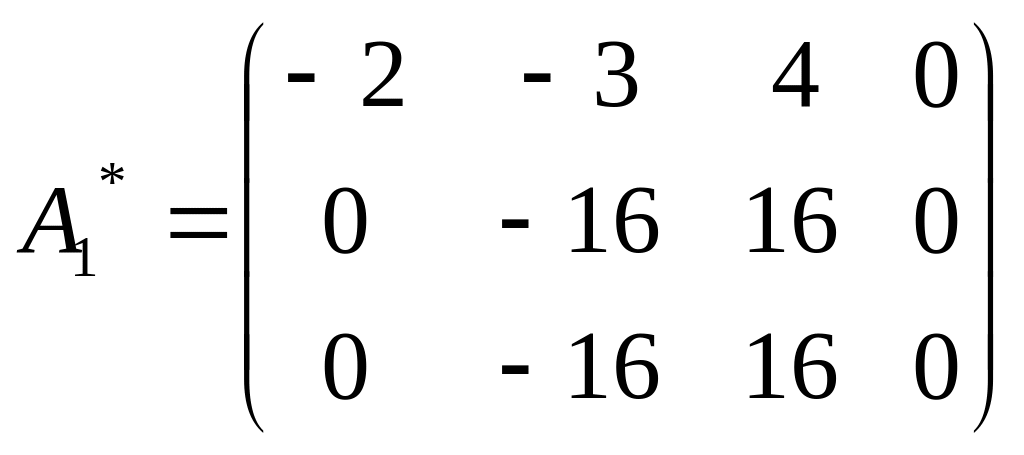
Вторую строку умножаем на -1 и прибавляем к третьей

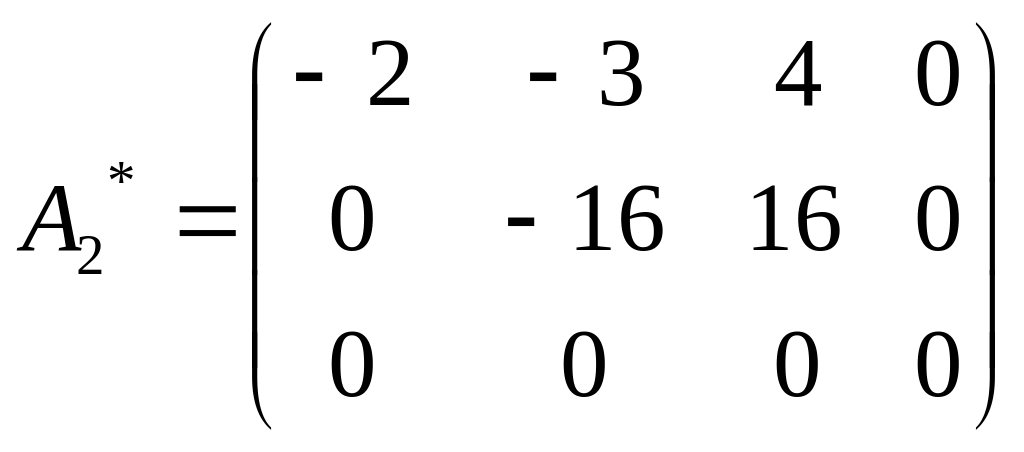
Возвращаемся к системе уравнений

Ранг матрицы равен 2. Число уравнений равно 2 (число линейно независимых строк), а число неизвестных 3. Поэтому фундаментальная система содержит только одно (3-2=1) решение. Переменные оставляем в левой части, а переменную переносим в правую часть

.

Полагаем , находим . Итак, собственному числу соответствует собственный вектор .

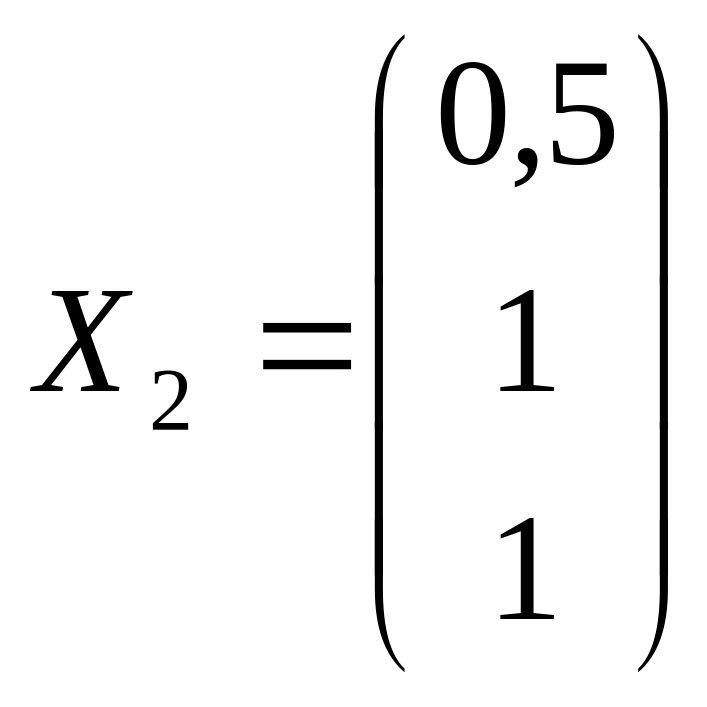. Чтобы избавиться от дроби, умножим собственный вектор на 2, получим собственный вектор с тем же самым собственным числом. В итоге собственному числу соответствует собственный вектор .

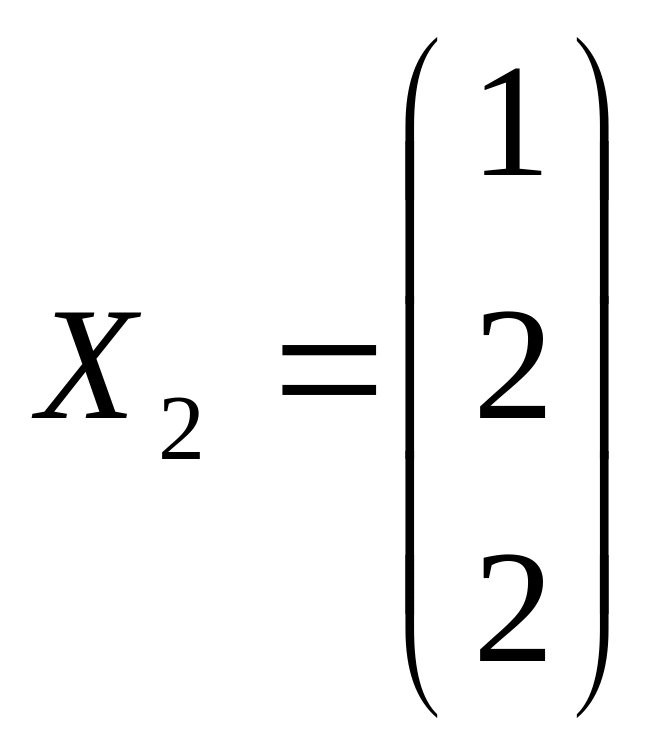1.13. Найти фундаментальную систему решений

Решение.

1. В системе выражаем r – базисных переменных (с отличным от нуля базисным минором) через свободные.

~

r(A) = r = 2

n = 4 k = n – r = 2

Фундаментальная система решений имеет k = 2

- базисные

- свободные

2. Поочередно заменяем n – r свободных переменных строками единичной матрицы .

1)

2)

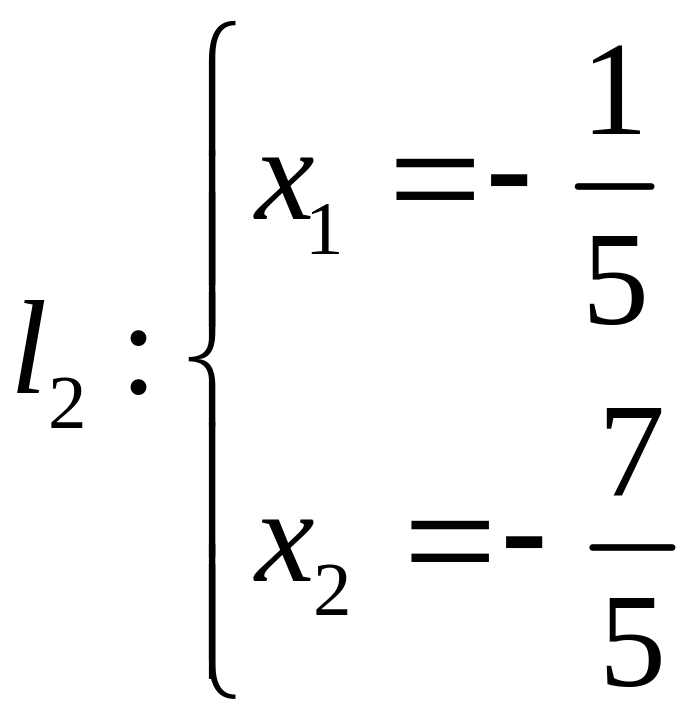
фундаментальная система решений

Общее решение

.

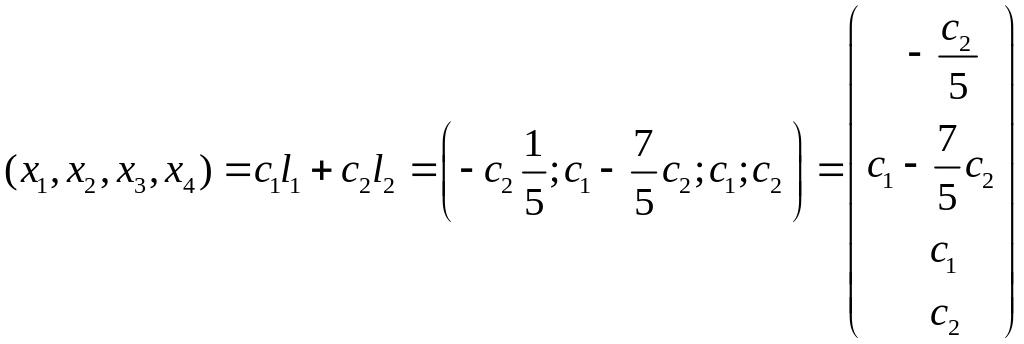2 Векторная алгебра.

2.1 Даны векторы (1; 2; 3), (-1; 0; 3), (2; 1; -1) и (3; 2; 2) в некотором базисе. Показать, что векторы , и образуют базис и найти координаты вектора в этом базисе.

Решение. Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:

линейно независимы.

Тогда .

Это условие выполняется, если определитель матрицы системы отличен от нуля.

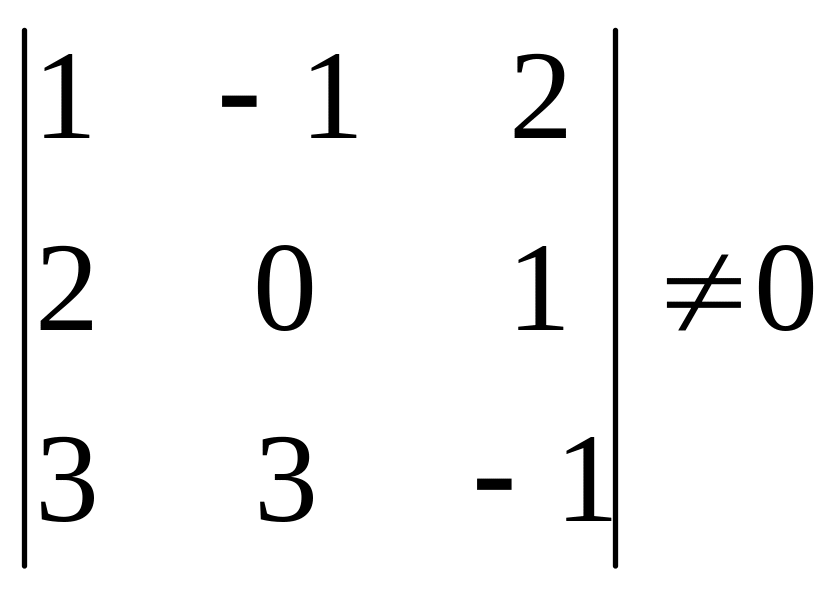
Для решения этой системы воспользуемся методом Крамера.

₁ =

;

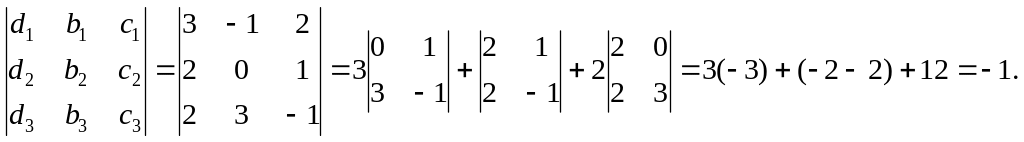
₂ =

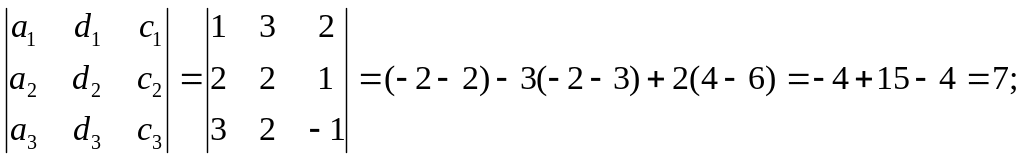
₃ =

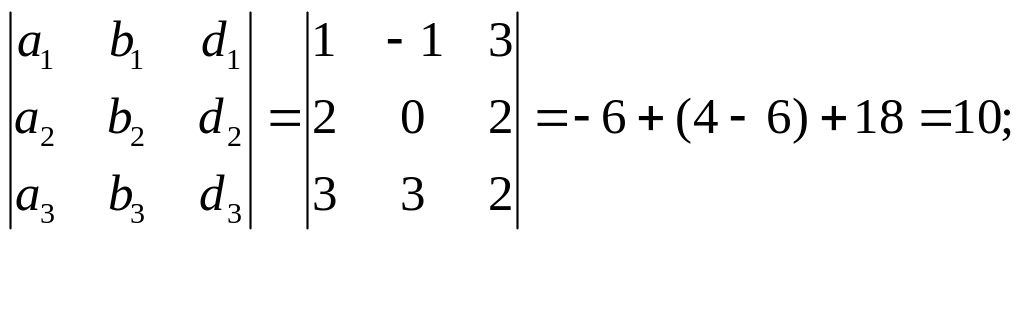
Итого, координаты вектора в базисе , , : = { -1/4, 7/4, 5/2}.

2.2 Найти (5 + 3 )(2 - ), если

Решение.

10  - 5  + 6  - 3  = 10 ,

т.к. .

2.3 Найти угол между векторами и , если

.

Решение.

= (1, 2, 3), = (6, 4, -2)

 = 6 + 8 – 6 = 8:

.

cos =

2.4 Найти векторное произведение векторов и

.

Решение.

= (2, 5, 1); = (1, 2, -3)

.

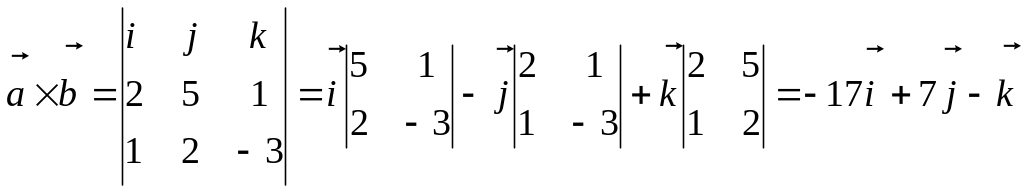2.5 Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0).

Решение.

2.6 Найти площадь параллелограмма, построенного на векторах , если

Решение.

(ед²).

2.7 Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.

Решение.

Найдем координаты векторов:

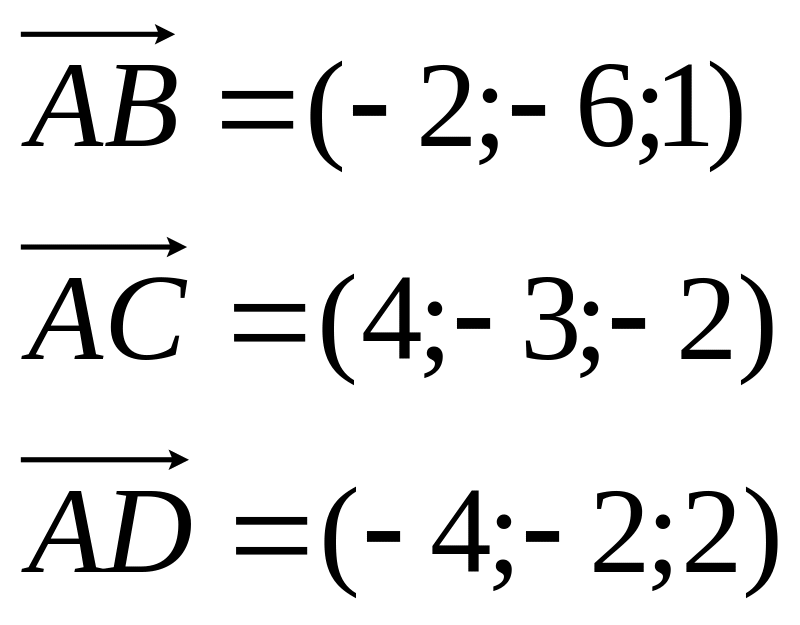
Найдем смешанное произведение полученных векторов:

,

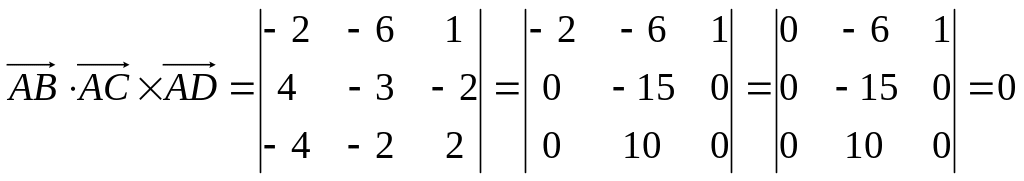Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.

2.8 Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0;0;1), B(2;3;5), C(6;2;3), D(3;7;2).

Решение.

Найдем координаты векторов:

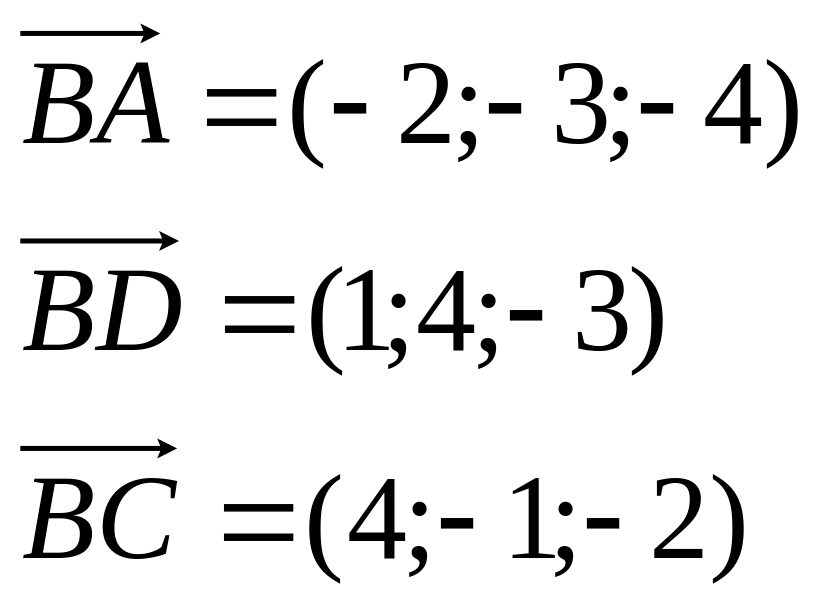
Объем пирамиды

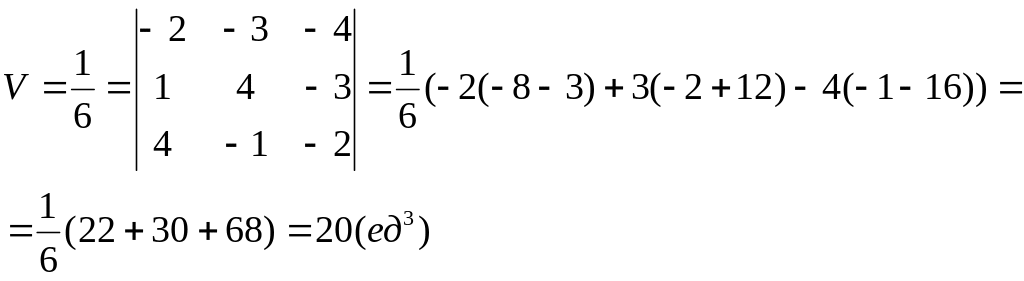
Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.

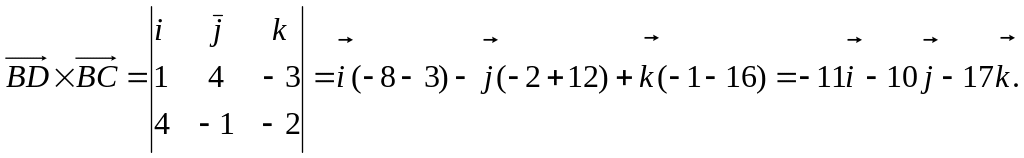
S_осн = (ед²)

Т.к. V = ; (ед)

2.9. Найти координаты вектора в пространстве R³ -- трехмерном векторном пространстве, в новом базисе , ,

Решение.

Выпишем матрицу перехода, ее столбцы -- это координаты новых базисных векторов

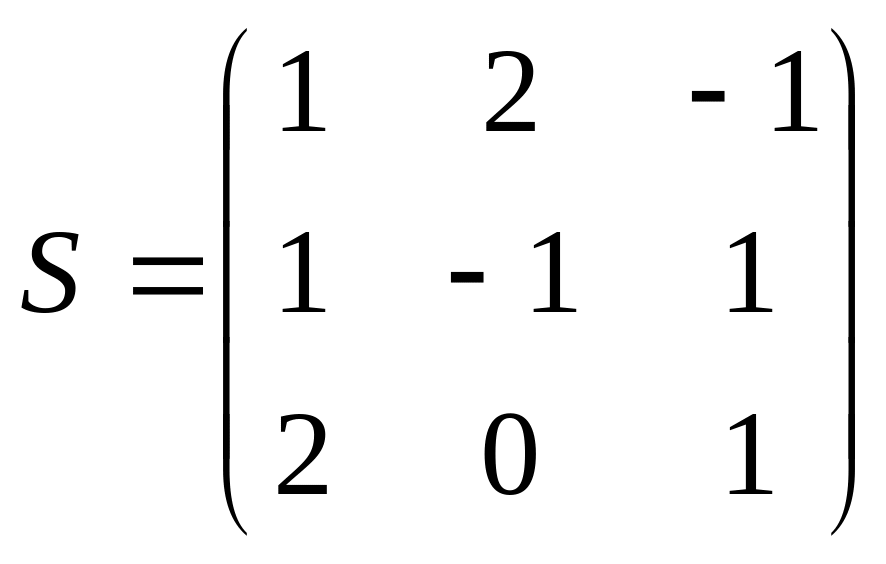
Пусть 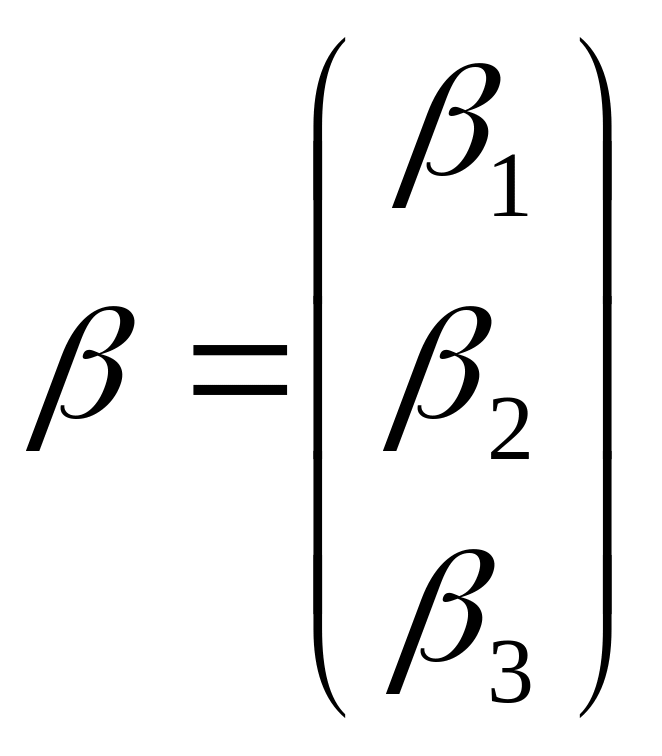- координатный столбец вектора в новом базисе. Тогда , откуда

Находим определитель

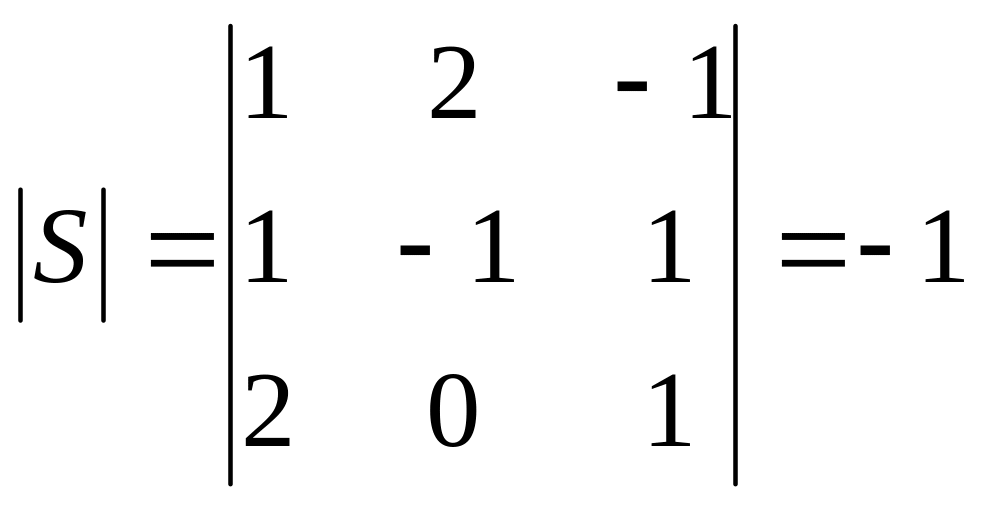
Находим алгебраические дополнения и обратную матрицу

.

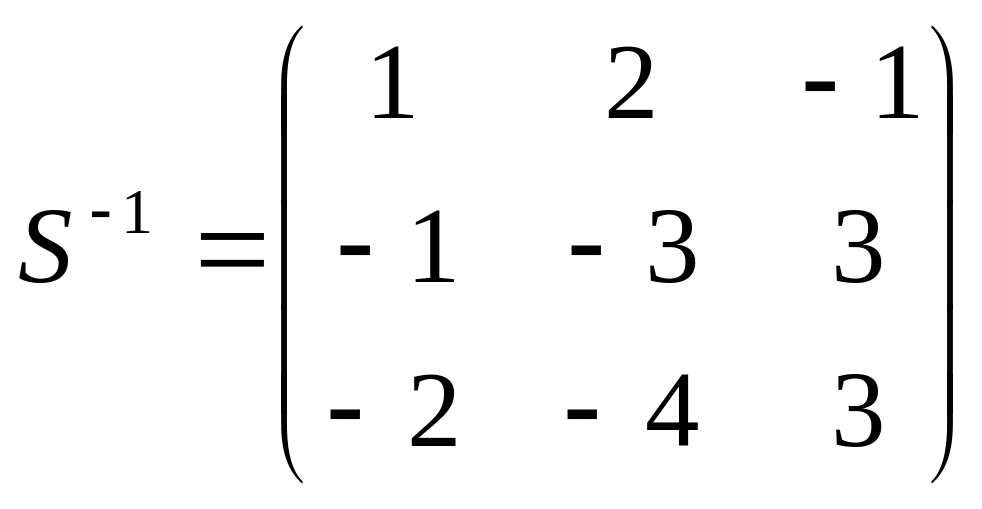Находим координаты вектора .

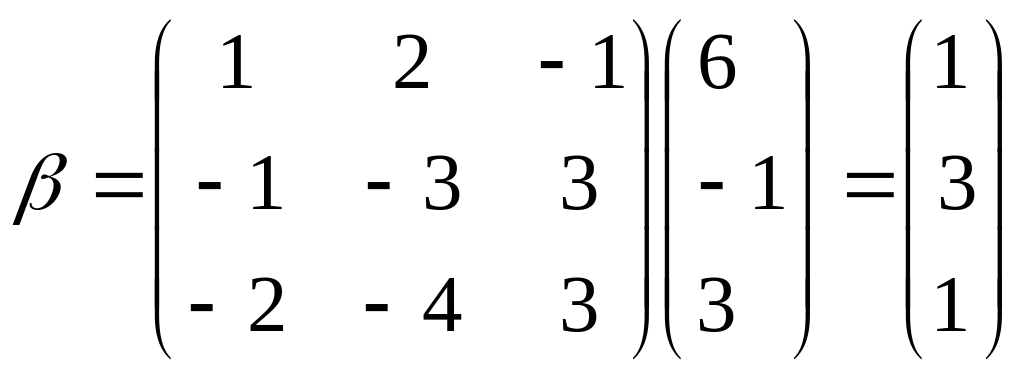Таким образом, новые координаты вектора : ,

Тот же самый результат можно было получить, записав систему уравнений

Решив эту систему, например, методом Гаусса, найдем новые координаты .

Модуль 2.

3 Аналитическая геометрия. Прямая на плоскости.

3.1 Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение.

Воспользуемся общим уравнением прямой . Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.

Получаем: 3 – 2 + C = 0, следовательно С = -1.

Итого: искомое уравнение: 3х – у – 1 = 0.

3.2 Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см².

Решение.

Уравнение прямой имеет вид: , a = b = 1; ab/2 = 8; a = 4; -4.

a = -4 не подходит по условию задачи.

Итого: или х + у – 4 = 0.

3.3 Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.

Решение.

Уравнение прямой имеет вид: , где х₁ = у₁ = 0; x₂ = -2; y₂ = -3.

3.4 Определить угол между прямыми: y = -3x + 7; y = 2x + 1.

Решение. Угол между двумя прямыми, заданными уравнениями с угловыми коэффициентами , определяется по формуле: .

k₁ = -3; k₂ = 2 tg = ;  = /4.

3.5 Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

Решение.

Находим уравнение стороны АВ: ; 4x = 6y – 6;

2x – 3y + 3 = 0;

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.

k = . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

Ответ: 3x + 2y – 34 = 0.

Кривые 2 порядка.

3.6 Найти координаты центра и радиус окружности, если ее уравнение задано в виде 2x² + 2y² – 8x + 5y – 4 = 0.

Решение. Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к каноническому виду. Для этого выделим полные квадраты:

x² + y² – 4x + 2,5y – 2 = 0

x² – 4x + 4 –4 + y² + 2,5y + 25/16 – 25/16 – 2 = 0

(x – 2)² + (y + 5/4)² – 25/16 – 6 = 0

(x – 2)² + (y + 5/4)² = 121/16

Отсюда находим О(2; -5/4); R = 11/4.

3.7 Составить уравнение эллипса, если его фокусы F₁(0; 0), F₂(1; 1), большая ось равна 2.

Решение. Уравнение эллипса имеет вид: . Расстояние между фокусами:

2c = , таким образом, a² – b² = c² = ½

по условию 2а = 2, следовательно а = 1, b =

Итого: .

3.8 Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением

Решение. Находим фокусное расстояние c² = 25 – 9 = 16.

Для гиперболы: c² = a² + b² = 16, e = c/a = 2; c = 2a; c² = 4a²; a² = 4;

b² = 16 – 4 = 12.

Итого: - искомое уравнение гиперболы.

3.9 На параболе у² = 8х найти точку, расстояние которой от директрисы равно 4.

Решение. Из уравнения параболы получаем, что р = 4.

r = x + p/2 = 4; следовательно:

x = 2; y² = 16; y = 4. Искомые точки: M₁(2; 4), M₂(2; -4).

3.10. Привести к каноническому виду уравнение второго порядка

.

Решение.

Матрица квадратичной формы имеет вид: .

Найдем ее собственные числа и собственные векторы. Составим характеристическое уравнение: , .

Для координат собственного вектора , соответствующего λ₁, получим с учетом нормировки: , откуда = . Аналогично найдем , = .

Составим матрицу перехода к новому базису, столбцами которой будут координаты собственных векторов: .

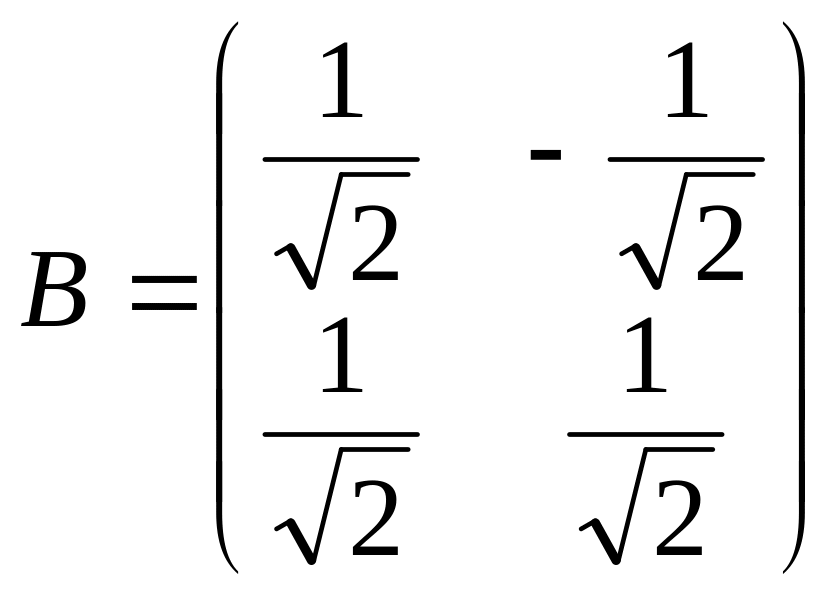Тогда .

Подставив эти выражения в исходное уравнение, получим его вид в новой системе координат: . Заметим, что коэффициентами при x² и y² являются λ₁ и λ₂.

Преобразуем полученное уравнение:

,

.

Зададим параллельный перенос формулами: .

Получим уравнение: , а после деления на 8: - каноническое уравнение гиперболы.

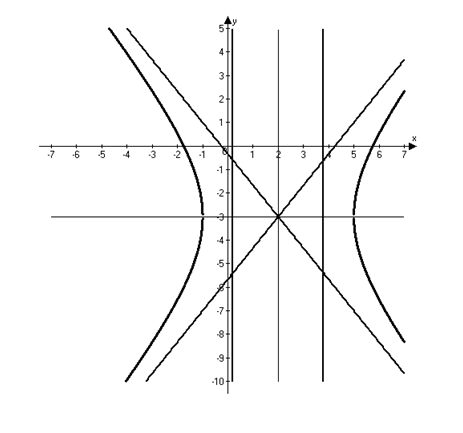
3.11. Определить тип кривой, заданной уравнением , ее параметры и сделать рисунок.

Решение.

Сгруппируем переменные: .

Дополним выражения, стоящие в скобках, до полного квадрата: ,

Получим: 

Уравнение определяет гиперболу с центром в точке и полуосями . Оси данной гиперболы будут лежать на прямых .

Определим параметр :

.

Тогда эксцентриситет будет равен: .

Асимптотами гиперболы будут прямые , или, после очевидных преобразований .

Директрисами гиперболы будут прямые , или, что то же самое, прямые .

3.12. Найти координаты точки М(-4;2) в новой системе координат, полученной поворотом осей на 30° и переносом начала координат в точку А(6;-2).

Решение.

Используем формулы перехода

.

У нас

.

Решаем систему, находим , т.е. .

Прямая и плоскость в пространстве.

3.13 Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость

Решение.

Таким образом, A = 4/13; B = -3/13; C = 12/13, воспользуемся формулой:

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

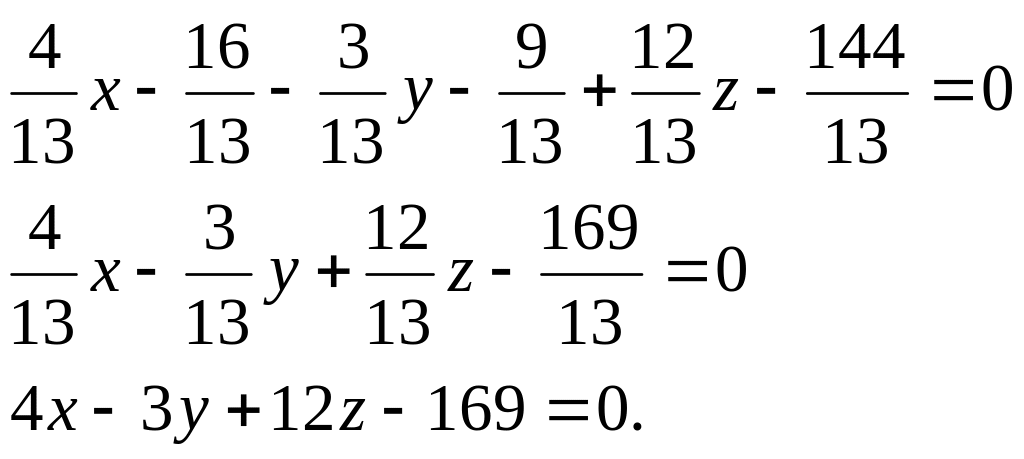
3.14 Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1) перпендикулярно плоскости х + у + 2z – 3 = 0.

Решение. Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости (A, B, C). Вектор (1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой, имеет вектор нормали (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то

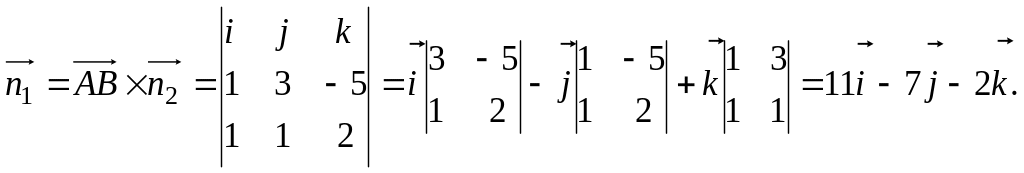
Таким образом, вектор нормали (11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 112 + 71 - 24 + D = 0; D = -21.

Итого, получаем уравнение плоскости: 11x - 7y – 2z – 21 = 0.

3.15 Привести к каноническому виду уравнение прямой, заданное в виде:

Решение.

Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда:

;

2x – 9x – 7 = 0;

x = -1; y = 3;

Получаем: A(-1; 3; 0).

Направляющий вектор прямой: .

Итого:

3.16 Даны координаты вершин пирамиды А₁(1; 0; 3), A₂(2; -1; 3), A₃(2; 1; 1), A₄(1; 2; 5).

1. Найти длину ребра А₁А₂.

Решение.

2. Найти угол между ребрами А₁А₂ и А₁А₄.

Решение.

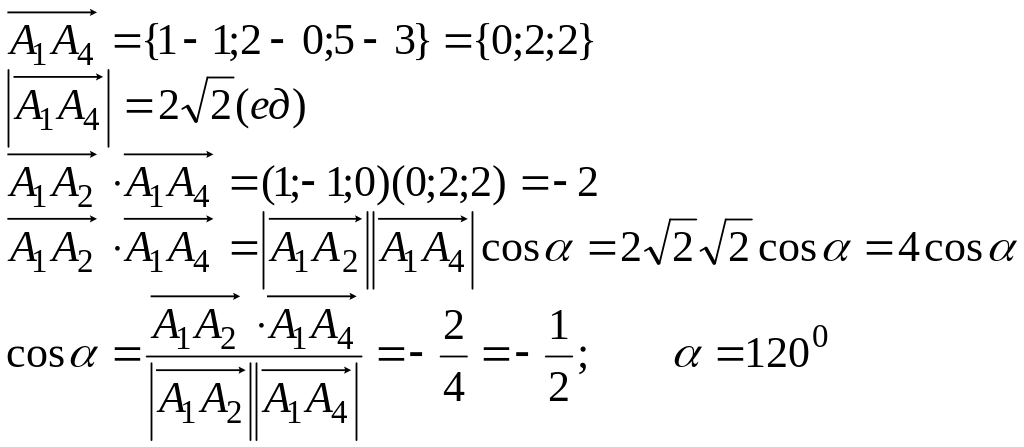
3. Найти угол между ребром А₁А₄ и гранью А₁А₂А₃.

Решение. Сначала найдем вектор нормали к грани А₁А₂А₃ как векторное произведение векторов и .

= (2-1; 1-0; 1-3) = (1; 1; -2);

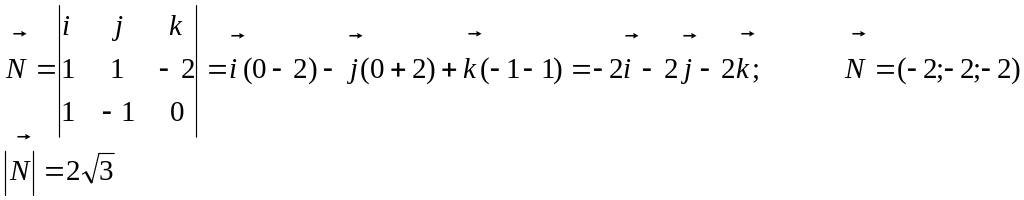
Найдем угол между вектором нормали и вектором .

-4 – 4 = -8.

Искомый угол  между вектором и плоскостью будет равен  = 90⁰ - .

4. Найти уравнение плоскости А₁А₂А₃.

Решение. Воспользуемся формулой уравнения плоскости, проходящей через три точки.

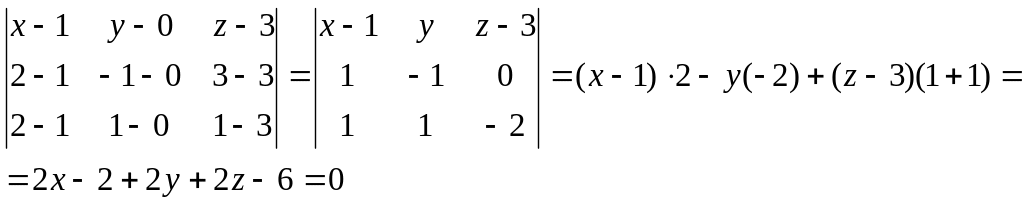
2x + 2y + 2z – 8 = 0

x + y + z – 4 = 0.