
- •Розділ і.
- •§1. Метод координат.
- •1.1. Декартова система координат. Координати точки.
- •1.2. Відстань між двома точками. Рівняння кола та сфери.
- •1.3. Ділення відрізка у даному відношенні.
- •1.4. Пряма лінія на площині.
- •1.5. Площина в просторі.
- •1.6. Пряма лінія в просторі.
- •1.7. „За числами бачити фігури”.
- •§2. Перетин прямих ліній і площин.
- •2.1. Знаходження точки перетину двох прямих ліній на площині.
- •2.2. Знаходження точки перетину трьох площин у просторі.
- •Нехай маємо три площини
- •2.3. Перетин двох прямих на площині; одна з прямих задана канонічним рівнянням.
- •2.4. Знаходження точки перетину прямої і площини.
- •§3. Вступ до векторної алгебри.
- •3.1. Поняття вільного вектора.
- •3.2. Арифметичні операції над векторами.
- •3.3. Координатне подання арифметичних операцій над векторами.
- •3.4. Поняття одиничного декартового базису. Розкладення векторів за базисом.
- •3.5. Скалярний добуток векторів, його обчислення і застосування.
- •3.6. Точки та їх радіус-вектори.
- •§4. Розв’язання задач лінійного програмування малої
- •4.1. Математична модель задачі лінійного програмування.
- •4.2. Розв’язання злп.
- •§5. Векторний добуток векторів, його обчислення та застосування.
- •5.1. Поняття векторного добутку.
- •5.2. Властивості векторного добутку.
- •5.3. Координатне подання векторного добутку.
- •5.4. Координатне подання векторного добутку в детермінантній формі.
- •5.5. Контрольна перевірка правильності обчислення векторного добутку.
- •5.6. Застосування векторного добутку.
- •§6. Змішаний добуток векторів, його обчислення та застосування.
- •6.1. Поняття змішаного добутку.
- •6.2. Властивості змішаного добутку.
- •6.3. Координатне подання змішаного добутку.
- •6.4. Застосування змішаного добутку.
- •§7. Метричні характеристики і взаємне розташування геометричних об’єктів.
- •7.1. Точки і прямі лінії на площині.
- •7.2. Точки і площини в просторі.
- •7.3. Точки і прямі в просторі.
- •7.4. Пряма і площина в просторі.
- •7.5. Площі.
- •7.7. Дві прямі в просторі.
1.2. Відстань між двома точками. Рівняння кола та сфери.
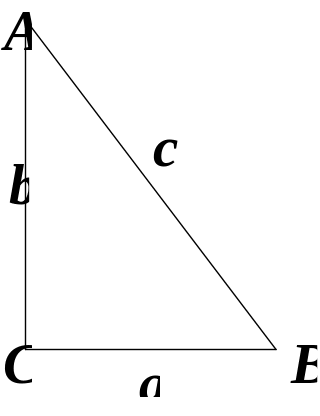
Формула відстані між двома точками, заданими своїми координатами, безпосередньо випливає з теореми Піфагора: квадрат довжини гіпотенузи прямокутного трикутника дорівнює сумі квадратів довжин його катетів:
![]()
Нехай маємо дві точки на координатній площині:
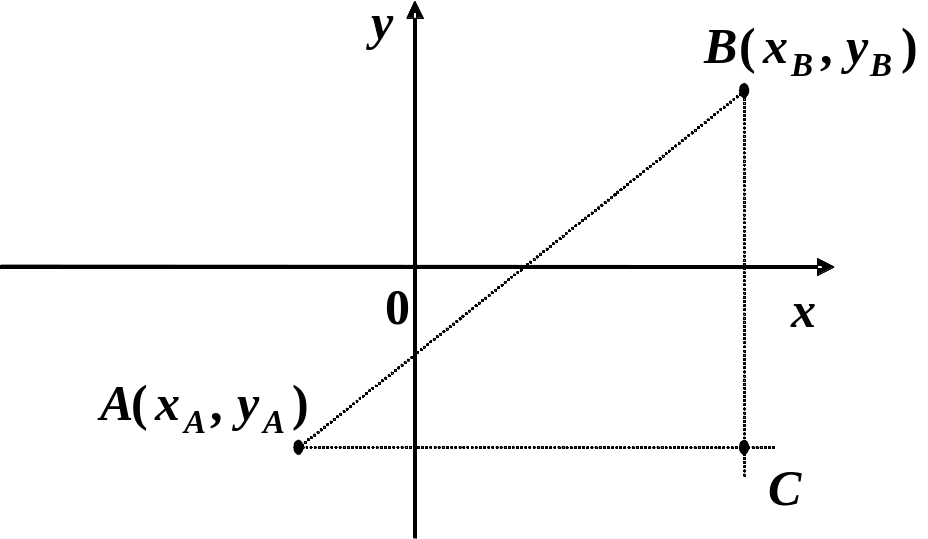
Сполучивши
точки
![]() і
і
![]() та провівши горизонтальну пряму через
точку
і вертикальну пряму через точку
,
отримаємо прямокутний трикутник
та провівши горизонтальну пряму через
точку
і вертикальну пряму через точку
,
отримаємо прямокутний трикутник ![]() .
Довжина гіпотенузи
.
Довжина гіпотенузи
![]() цього трикутника — це відстань між
точками
і
.
Довжина катета
цього трикутника — це відстань між
точками
і
.
Довжина катета
![]() дорівнює
дорівнює
![]() ;
довжина катета
;
довжина катета
![]() дорівнює
дорівнює
![]() .
Позначимо через
.
Позначимо через
![]() відстань між точками
і
.
З теореми Піфагора маємо:
відстань між точками
і
.
З теореми Піфагора маємо:
![]() ,
,
звідки випливає формула
![]()
Ця формула дозволяє
“перекласти” на аналітичну мову
означення кола і сфери. Коло
— це геометричне місце точок площини,
що розташовані на деякій фіксованій
відстані (яка називається радіусом),
від деякої фіксованої точки (яка
називається центром).
Нехай заданий радіус дорівнює
![]() ,
центром кола є точка
,
центром кола є точка
![]() ,
а “біжучою” точкою кола є
,
а “біжучою” точкою кола є
![]() .
.
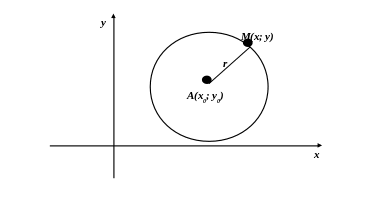
Тоді, з використанням формули відстані між двома точками, означення кола перейде у рівняння:
![]() .
.
Аналогічні формули
мають місце для тривимірного простору.
А саме, якщо
![]() та
та
![]() — задані
просторові точки, то відстань
між ними обчислюється за формулою:
— задані
просторові точки, то відстань
між ними обчислюється за формулою:
![]() .
.
Для виведення цієї формули замість прямокутного трикутника треба розглядати прямокутний паралелепіпед та його діагональ.
Якщо в означенні кола замінити слово площини на слово простору, — ми отримаємо означення сфери та її рівняння:
![]() .
.
1.3. Ділення відрізка у даному відношенні.
Формула ділення відрізка в заданому відношенні грунтується на теоремі Фалеса: якщо дві дані прямі перетнути трьома (або більшою кількістю) паралельних прямих, то відношення довжин відрізків, що відтинаються цими паралельними прямими на одній з даних прямих, дорівнює відношенню довжин відповідних відрізків на другій з даних прямих.

![]()
Розглянемо задачу
ділення
заданого відрізку прямої на координатній
площині на
![]() рівних частин.
Це означає: за заданими координатами
кінців відрізку
рівних частин.
Це означає: за заданими координатами
кінців відрізку
![]() ,
,
![]() (розглядаємо задачу для випадку площини)
знайти координати точок ділення
(розглядаємо задачу для випадку площини)
знайти координати точок ділення
![]() ,
,
![]() ,
…,
,
…,
![]() ,
так що
,
так що
![]() .
.
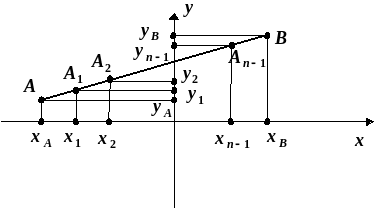
Виходячи з теореми
Фалеса, відрізки
![]() та
та
![]() ,
які є проекціями даного відрізку на
координатні осі, також поділені на
,
які є проекціями даного відрізку на
координатні осі, також поділені на
![]() рівних частин. Отже,
рівних частин. Отже,
![]() ,
,
![]() .
.
Звідси,
![]() ,
,
![]() ;
;
![]() ,
.
,
.
Остаточно маємо координати точок ділення:
![]() ,
,
![]() ,
,
………………………
![]() ,
,
………………………
![]() .
.
Тепер розглянемо
задачу ділення
заданого відрізку прямої на координатній
площині у заданому відношенні
![]() .
Це означає: за заданими координатами
кінців відрізку
,
знайти координати точки ділення
.
Це означає: за заданими координатами
кінців відрізку
,
знайти координати точки ділення
![]() цього відрізку так, щоби відношення
довжин відрізків
та
цього відрізку так, щоби відношення
довжин відрізків
та
![]() дорівнювало
:
дорівнювало
:
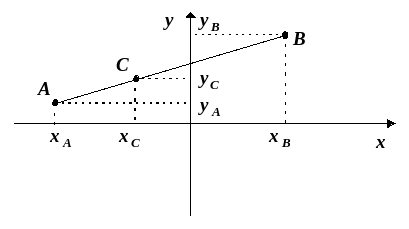
Треба
знайти
координати
точки
![]() ,
виходячи
з
того,
що
відношення
довжин
відрізків
,
виходячи
з
того,
що
відношення
довжин
відрізків
![]() та
та
![]() має
дорівнювати
:
має
дорівнювати
:
![]() .
.
Повторюючи міркування з попередньої задачі, маємо:
![]()
![]() .
.
Аналогічно отримуємо
![]() .
.
Зокрема, якщо треба
поділити відрізок
![]() навпіл, то точка ділення
навпіл, то точка ділення
![]() буде мати такі координати:
буде мати такі координати:
![]() ,
,
![]() .
.
Аналогічні формули мають місце для випадку простору.
