5.3. Координатне подання векторного добутку.
З’ясуємо, як обчислити координати векторного добутку, якщо відомі координати векторів-множників. Для цього ми використаємо розкладання векторів-множників за одиничним базисом простору.
Нехай вектори і задані своїми координатами:
.
Розкладемо вектори
і
за одиничним декартовим базисом
:
Тоді
.
Використовуючи алгебраїчні властивості векторного добутку ми можемо, обчислюючи векторний добуток двох сум, перемножувати доданки почленно:
Як ми вже знаємо,
векторний добуток колінеарних векторів
рівний нулю. Так само рівний нулю й
векторний добуток однакових множників:
Це спрощує вираз для
, зменшуючи кількість доданків до шести:
користуючись властивостями однорідності та антикомутативності векторного добутку, здійснюємо подальше спрощення виразу:
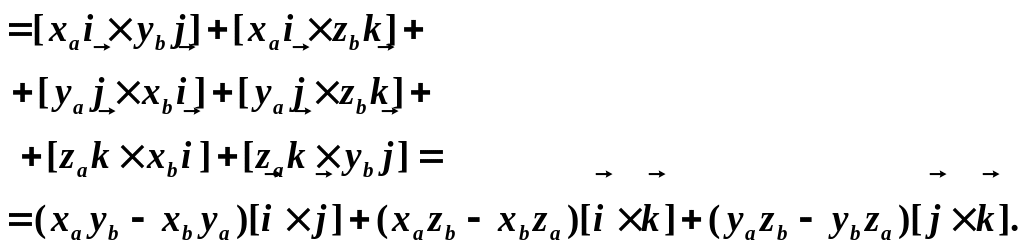
Для отримання
остаточного вигляду розглядуваного
виразу залишилось з’ясувати, чому
дорівнюють векторні добутки відповідних
пар базисних векторів:
.
Розглянемо векторний добуток
.
Модуль вектора
дорівнює площі паралелограма, побудованого
на векторах
та
.
Цей паралелограм є квадратом зі стороною,
рівною одиниці, отже його площа рівна
одиниці. Таким чином,
є одиничний вектор. Беручи до уваги, що
вектор
повинен бути перпендикулярним до
векторів
та
і напрямленим згідно правилу
правої руки (якщо
вектори
зведені до спільного початку, то вектор
повинен бути направлений так, як
направлений середній палець правої
руки, великий палець якої направлений
по першому співмножнику (тобто по вектору
),
а вказівний— по другому (тобто по вектору
)),
легко зрозуміти, що він співпадає з
третім базисним вектором
,
тобто
.
Міркуючи аналогічно, отримаємо:
.
Отже, остаточно,
5.4. Координатне подання векторного добутку в детермінантній формі.
Для отримання
формули обчислення координат векторного
добутку через координати векторів-множників
використаємо поняття визначника (або
детермінанта) другого порядку (див.
§2).
Згадаємо: визначник другого порядку –
це визначник квадратної
матриці
,
позначається
або
,
–це число,
яке обчислюється за формулою:
=
.
Теорема (про координатне подання векторного добутку в детермінантній формі). Якщо вектори і задані своїми координатами:
,
то векторний
добуток векторів
і
визначається формулою:
.
Доведення очевидне.
Зауваження. Для зручності обчислення векторного добутку корисно координати заданих векторів записати спочатку у вигляді наступної таблиці:
.
Закриваючи тут спочатку перший стовпчик, потім другий і третій, ми отримаємо послідовно три визначника другого порядку; обчислюючи їх і взявши другий зі знаком мінус, ми таким чином знайдемо три координати векторного добутку .
Формулі обчислення координат векторного добутку за координатами векторів-множників можна надати ще більш компактного вигляду:
.
Дійсно, якщо розгорнути цей визначник (див. §9) за елементами першого рядка, то отримаємо попередню формулу.
Приклад.
Дано 2 вектори
і
.
Знайти координати векторного добутку
.
Розв’язання. Складаємо таблицю:
.
Закриваючи послідовно стовпчики цієї таблиці, ми отримаємо три визначники другого порядку, обчислюючи їх і, взявши другий зі знаком мінус, знайдемо шукані проекції:
