
- •Глава 9 обтекание тел вращения сверхзвуковым потоком
- •Осесимметричное обтекание острого конуса
- •Несимметричное обтекание конуса сверхзвуковым потоком
- •Приближенный метод расчета. Метод касательных конусов
- •Определение нормальной и продольной силы по распределению давления
- •Нормальная сила и момент тангажа для тонких тел вращения
- •Особенности околозвуковых течений
- •Особенности гиперзвуковых течений
- •Изменение параметров газа при возмущении скорости
- •Приближенная теория Ньютона
- •Контрольные вопросы и задания
Нормальная сила и момент тангажа для тонких тел вращения
Рассмотрим обтекание тонкого удлиненного тела вращения при малом угле атаке. В этом случае возмущенный поток в окрестности тела мало отличается от невозмущенного. По методу малых возмущений потенциал скорости потока удовлетворяет линейному дифференциальному уравнению и может быть представлен в виде суммы трех составляющих (рис. 9.10):
![]() ,
,
где
![]() потенциал невозмущенного потока;
потенциал невозмущенного потока;
![]() – потенциал скорости возмущения при
осесимметричном
– потенциал скорости возмущения при
осесимметричном
![]() обтекании тела потоком со скоростью
обтекании тела потоком со скоростью
![]()
![]() – потенциал, возникающий при поперечном
обтекании тела потоком со скоростью
– потенциал, возникающий при поперечном
обтекании тела потоком со скоростью
![]() .
.
Согласно линейной теории потенциал обтекания тонкого тела при сверхзвуковых скоростях описывается уравнением
 .
.

а б в
Рис. 9.10. Тонкое тело вращения при малом угле атаки:
а
–
![]() ;
б –
;
б –
![]() в –
в –
![]()
В
безразмерных координатах (
,
![]() и
и
![]() ,
где
,
где
![]() – диаметр миделевого сечения;
– длина тела) уравнение для потенциала
перепишется в виде
– диаметр миделевого сечения;
– длина тела) уравнение для потенциала
перепишется в виде
 . (9.16)
. (9.16)
Для
тонких тел
![]() << 1, и, пренебрегая первым слагаемым
в выражении (9.16) ввиду его малости,
запишем следующее:
<< 1, и, пренебрегая первым слагаемым
в выражении (9.16) ввиду его малости,
запишем следующее:
 .
(9.17)
.
(9.17)
Уравнение
(9.17) есть ни что иное, как уравнение
Лапласа – уравнение неразрывности для
плоского
потенциального
течения несжимаемой
жидкости.
То есть поток в плоскости ZOY
поперечного сечения тонкого тела можно
считать двумерным, совпадающим с
поперечным обтеканием цилиндра радиусом,
равным местному радиусу тела вращения
![]() ,
несжимаемой жидкостью. Кроме того, из
уравнения (9.17) следует также, что потенциал
обтекания тонкого тела не зависит от
числа
.
,
несжимаемой жидкостью. Кроме того, из
уравнения (9.17) следует также, что потенциал
обтекания тонкого тела не зависит от
числа
.
В
результате некоторых преобразований
уравнения (9.17) и интегрирования по углу
![]() получим выражение для нормальной силы,
действующей на элемент тела вращения
длиной
получим выражение для нормальной силы,
действующей на элемент тела вращения
длиной
![]() :
:
![]() , (9.18)
, (9.18)
где
![]() .
Отсюда следует, что нормальная сила
.
Отсюда следует, что нормальная сила
![]() появляется только на участках с переменной
площадью поперечного сечения. Знак силы
зависит от знака производной
появляется только на участках с переменной
площадью поперечного сечения. Знак силы
зависит от знака производной
![]() (рис. 9.11).
(рис. 9.11).
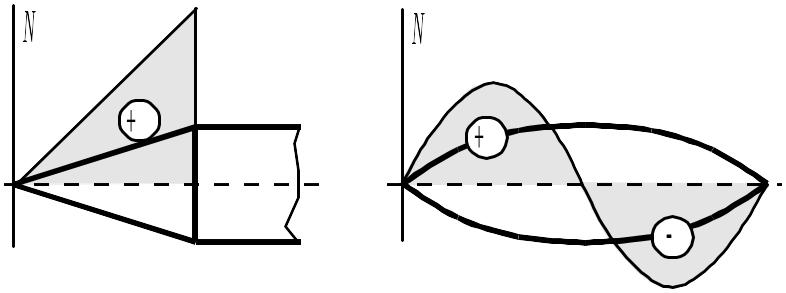
а б
Рис. 9.11. Распределение нормальной силы по поверхности конуса:
а – цилиндрического тела; б – параболического тела
Носовая
часть корпуса
![]() создает положительную нормальную силу,
а суживающаяся хвостовая часть
создает положительную нормальную силу,
а суживающаяся хвостовая часть
![]() – отрицательную нормальную силу, тогда
как цилиндрический отсек, для которого
– отрицательную нормальную силу, тогда
как цилиндрический отсек, для которого
![]() ,
при обтекании тела идеальной жидкостью
не создает нормальной силы.
,
при обтекании тела идеальной жидкостью
не создает нормальной силы.
Нормальная суммарная сила для тонкого тела вращения равна
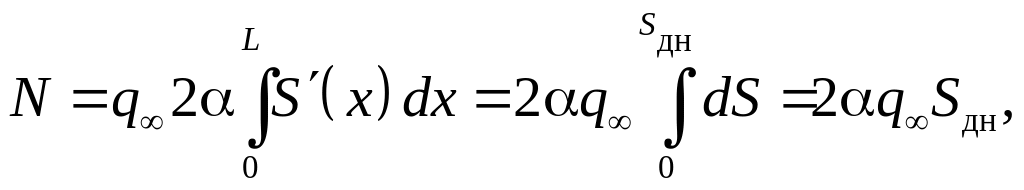
а коэффициент нормальной силы равен
![]() , (9.19)
, (9.19)
где
 – относительная площадь донного среза
(угол
измеряется в радианах). Для носовой
части
– относительная площадь донного среза
(угол
измеряется в радианах). Для носовой
части
![]() и
и
![]() независимо от формы носовой части и
числа Маха.
независимо от формы носовой части и
числа Маха.
М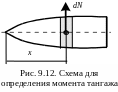 омент
элементарной нормальной силы относительно
вершины тела (рис. 9.12) – момент тангажа
– равен
омент
элементарной нормальной силы относительно
вершины тела (рис. 9.12) – момент тангажа
– равен
![]() Знак «минус» в этой формуле говорит о
том, что создаваемый момент – это момент
на пикирование:
Знак «минус» в этой формуле говорит о
том, что создаваемый момент – это момент
на пикирование:
![]() ,
,
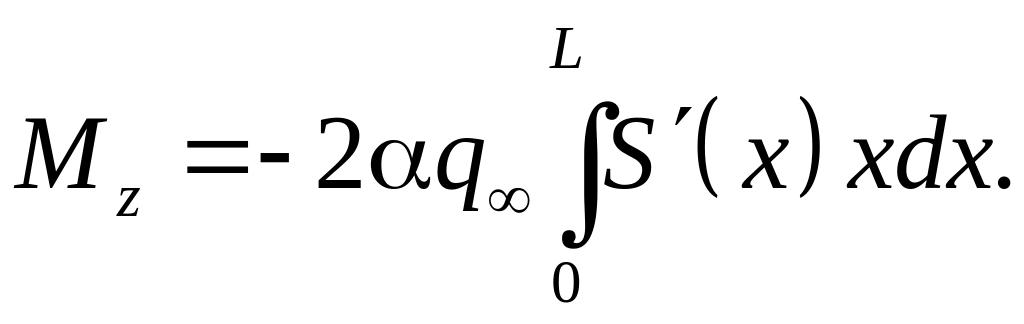
Коэффициент момента равен
 ,
,
т.
е.
 ,
где
,
где
![]() – объем носовой части.
– объем носовой части.
Особенности околозвуковых течений
Околозвуковым называется течение, если в его поле имеются одновременно два вида областей: дозвуковые и сверхзвуковые.
П ри
непрерывном увеличении числа Маха
невозмущенного потока от нуля можно
считать, что околозвуковой
диапазон начинается там, где наибольшее
из местных чисел Маха достигает единицы,
и кончается там, где достигает единицы
наименьшее из чисел Маха.
ри
непрерывном увеличении числа Маха
невозмущенного потока от нуля можно
считать, что околозвуковой
диапазон начинается там, где наибольшее
из местных чисел Маха достигает единицы,
и кончается там, где достигает единицы
наименьшее из чисел Маха.
Для
тонких тел вращения область околозвуковых
скоростей определяется интервалом
чисел
![]() .
Для двумерных течений диапазон
околозвуковых чисел Маха зависит от
относительной толщины тела
.
Для двумерных течений диапазон
околозвуковых чисел Маха зависит от
относительной толщины тела
![]() (рис. 9.13). То же относится и к
конус-цилиндрическим телам (для них
(рис. 9.13). То же относится и к
конус-цилиндрическим телам (для них
![]() ).
).
Некоторые
общие свойства околозвуковых течений
удобно рассматривать на примере обтекания
простого клина (рис. 9.14). При числе
![]() в угловой точке клина впервые достигается
скорость потока, равная скорости звука.
При обтекании угла происходит разрежение,
т. е. ускорение потока. Звуковая линия
и веер волн разрежения начинаются в
угловой точке.
в угловой точке клина впервые достигается
скорость потока, равная скорости звука.
При обтекании угла происходит разрежение,
т. е. ускорение потока. Звуковая линия
и веер волн разрежения начинаются в
угловой точке.
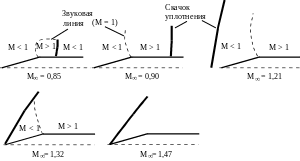
Рис. 9.14. Обтекание клина околозвуковым потоком
При
увеличении скорости потока и приближении
числа
к единице зона местных сверхзвуковых
скоростей за угловой точкой расширяется
в продольном и поперечном направлениях.
Скачок уплотнения, замыкающий местную
сверхзвуковую область, смещается вниз
по потоку. В то же время в отрицательной
«бесконечности» (в набегающем потоке)
зарождается новый скачок уплотнения,
который при увеличении числа
приближается к вершине клина и достигает
ее. Таким образом, если при
![]() местная сверхзвуковая зона располагается
перед скачком уплотнения, то при
местная сверхзвуковая зона располагается
перед скачком уплотнения, то при
![]() она располагается за ним.
она располагается за ним.
Околозвуковое обтекание клина и конуса имеет общие особенности:
Звуковая скорость не может быть достигнута на каком-либо плоском участке поверхности. Во всем околозвуковом диапазоне скоростей звуковая скорость достигается вблизи угловой точки тела.
При числе
 местное число Маха становится постоянным,
т. е.
местное число Маха становится постоянным,
т. е.
 .
Это значит, что местные числа Маха на
поверхности клина или конуса при
.
Это значит, что местные числа Маха на
поверхности клина или конуса при
 остаются постоянными. Это явление
называется законом
стабилизации для трансзвуковых течений
(например, для конуса с
остаются постоянными. Это явление
называется законом
стабилизации для трансзвуковых течений
(например, для конуса с
 диапазон постоянства определяется
значениями чисел Маха
диапазон постоянства определяется
значениями чисел Маха
 ).
).
О сесимметричный
поток у конуса имеет некоторые отличия
от потока около клина. Как уже говорилось,
при сверхзвуковом обтекании конуса, в
отличие от клина, параметры потока
одинаковы только на конических
поверхностях (а не во всей области между
скачком и поверхностью). При обтекании
конуса поток в области между скачком и
конусом претерпевает дополнительное
изоэнтропическое сжатие. То есть при
некоторых малых сверхзвуковых числах
Маха поток за скачком еще сверхзвуковой,
а ближе к поверхности конуса может стать
дозвуковым (рис. 9.15). Таким образом,
наблюдается плавный переход от
сверхзвуковых скоростей к дозвуковым.
За скачком уплотнения может существовать
дозвуковая зона, вклинивающаяся в
область сверхзвукового течения и
примыкающая к поверхности конуса. При
еще меньших сверхзвуковых скоростях
поток уже не является коническим.
сесимметричный
поток у конуса имеет некоторые отличия
от потока около клина. Как уже говорилось,
при сверхзвуковом обтекании конуса, в
отличие от клина, параметры потока
одинаковы только на конических
поверхностях (а не во всей области между
скачком и поверхностью). При обтекании
конуса поток в области между скачком и
конусом претерпевает дополнительное
изоэнтропическое сжатие. То есть при
некоторых малых сверхзвуковых числах
Маха поток за скачком еще сверхзвуковой,
а ближе к поверхности конуса может стать
дозвуковым (рис. 9.15). Таким образом,
наблюдается плавный переход от
сверхзвуковых скоростей к дозвуковым.
За скачком уплотнения может существовать
дозвуковая зона, вклинивающаяся в
область сверхзвукового течения и
примыкающая к поверхности конуса. При
еще меньших сверхзвуковых скоростях
поток уже не является коническим.
В
околозвуковом диапазоне скоростей
появляется дополнительное волновое
сопротивление, которое приводит к
резкому возрастанию полного сопротивления
тела (так называемый волновой кризис).
Следует отметить, что заметное возрастание
коэффициента сопротивления за счет
волнового сопротивления проявляется
при числах Маха
![]() .
.
Э кспериментальные
данные для тел вращения показывают
следующее:
кспериментальные
данные для тел вращения показывают
следующее:
Коэффициент лобового сопротивления достигает своего максимума при числах Маха, несколько больших числа , в интервале
 .
.Доминирующее влияние на величину
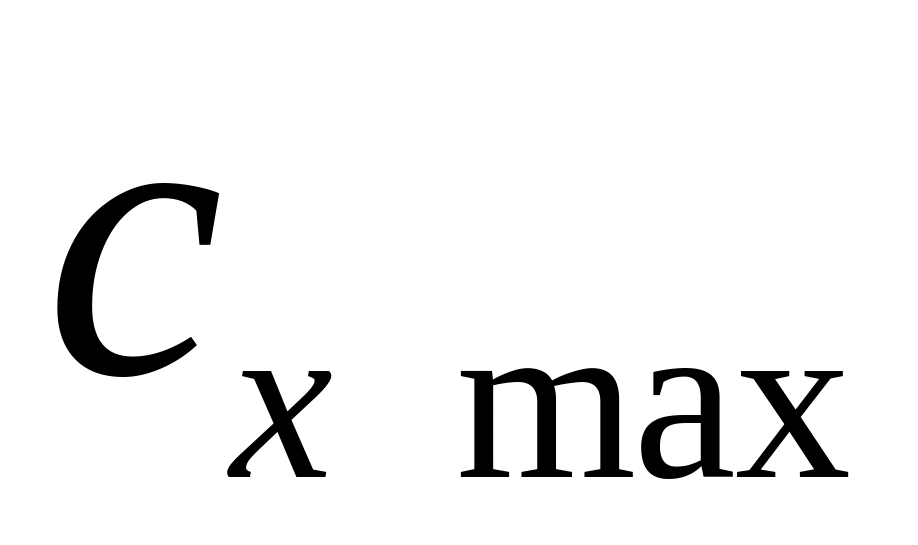 оказывает форма головной части (рис.
9.16).
оказывает форма головной части (рис.
9.16).
При числах для определения характеристик ЛА в основном используют результаты эксперимента. При числах Маха, близких к единице (область действия закона трансзвуковой стабилизации), расчет характеристик ведут по данным для с учетом их градиента. Например, по известным данным для при можно рассчитать коэффициент сопротивления для чисел Маха . Или наоборот, можно экстраполировать данные для чисел Маха, близких к единице, на число Маха .
