Глава 9 обтекание тел вращения сверхзвуковым потоком
Коническим называют поток, в котором параметры газа на конической поверхности сохраняются постоянными. Они изменяются только при переходе с одной конической поверхности на другую.
Осесимметричным называют течение, обладающее симметрией относительно оси тела. В этом случае течение газа во всех меридиональных плоскостях одинаково, и движение газа можно изучать как плоское в одной из меридиональных плоскостей.
Осесимметричное обтекание острого конуса
Рассмотрим
осесимметричное (
)
обтекание конуса с углом полураствора
сверхзвуковым потоком.
Результаты решения задачи осесимметричного обтекания острого конуса используются в следующих случаях:
а) для определения коэффициента волнового сопротивления конических головных частей корпусов ЛА;
б)
в качестве исходных данных для численного
расчета обтекания конусов при
;
в) в качестве начальной точки при расчете обтекания тел с криволинейной образующей;
г) для приближенного расчета распределения давления по поверхности тел более сложной формы.
П
ри
симметричном обтекании конуса с углом
полураствора
(
при заданном числе Маха
)
перед ним возникает присоединенный
конический скачок уплотнения с вершиной
в вершине конуса (рис. 9.1). Задача расчета
обтекания конуса сводится к нахождению
угла полураствора конического скачка
и поля скоростей (и давлений) между
скачком уплотнения и конусом. Поскольку
поток около конуса осессимметричный,
то будем рассматривать одну меридиональную
плоскость. Довольно просто убедиться,
что для всех плоскостей, перпендикулярных
продольной оси конуса, граничные условия
(при
и
)
одинаковы, и течения между конусом и
скачком уплотнения геометрически
подобны. То есть в сходственных точках
этих сечений параметры потока (
,
)
одинаковы. Геометрическим местом
сходственных точек являются конические
поверхности, расположенные между
поверхностью конуса и скачком уплотнения.
Течения подобного рода называются
коническими.
Задача
решается в полярной системе координат
с полюсом в вершине конуса. Зафиксируем
некоторую промежуточную коническую
поверхность с углом полураствора
.
Вследствие конического характера
течения составляющие скорости потока
на этой поверхности не зависят от
координаты
:
.
Кроме
того, ввиду прямолинейности образующей
скачка уплотнения при переходе через
фронт скачка по любой линии тока энтропия
возрастает одинаково (потери механической
энергии одинаковы), и течение между
конусом и скачком является изоэнтропическим
и потенциальным
(безвихревым). Следовательно, составляющие
вектора скорости можно записать через
потенциал скорости
:
.
Для осесимметричного конического потока
потенциал скорости можно представить
в виде
.
Тогда составляющие скорости равны
и
.
(9.1)
Исключив
из выражений (9.1), получим первое уравнение
для определения составляющих скорости
в виде
.
(9.2)
Вторым
уравнением, связывающим искомые величины
,
является уравнение неразрывности
,
которое для осесимметричного
установившегося течения можно записать
в сферических координатах:
или
.
(9.3)
Исключим
из выражения (9.3)
.
Поскольку течение между конусом и
скачком изоэнтропическое, воспользуемся
формулами изоэнтропического течения
(4.9)
и
.
Продифференцировав выражение для
плотности и учитывая, что
,
произведем замены с учетом выражения
(9.2):
.
После подстановки этого выражения в
уравнения (9.3) получаем следующее:
.
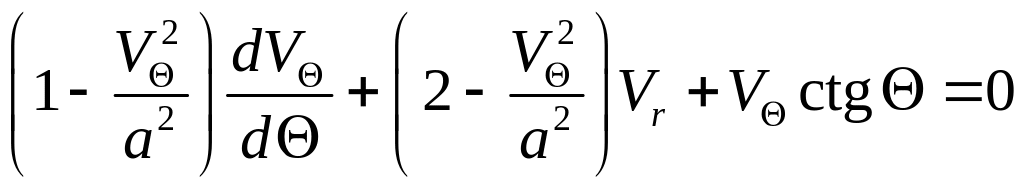Из этого равенства получаем второе
уравнение для расчета
и
.
В итоге получаем систему двух уравнений:
(9.4)
Эта система дифференциальных уравнений определяет все поле скоростей между скачком уплотнения и конусом. Для решения системы необходимо задать граничные условия. В данной задаче имеем следующие граничные условия:
1)
на поверхности конуса, где
нормальная составляющая вектора скорости
равна
(из условия непротекания), тогда из
второго уравнения системы
,
т. е. составляющая скорости
направлена по касательной к поверхности
конуса и равна скорости на поверхности
конуса:
;
2)
на поверхности скачка уплотнения, где
составляющие скорости
и
должны удовлетворять основным соотношениям
для косого скачка уплотнения (см. гл.
6):
а)
касательная составляющая скорости при
переходе через скачок уплотнения не
изменяется:
;
б)
нормальная составляющая
(она же
)
должна удовлетворять формуле Прандтля
для косого скачка уплотнения:
. (9.5)
Знак «минус» в левой части явился следствием того, что положительным считается направление в сторону увеличения угла , поэтому составляющая скорости , направленная к поверхности конуса, отрицательная.
Систему
дифференциальных уравнений при заданных
граничных условиях можно решить методом
численного интегрирования. Интегрирование
можно начать как с поверхности конуса,
задаваясь значением
и
,
так и с поверхности скачка, задаваясь
углом
и числом Маха
(скоростью
).
В первом случае в результате решения
системы находим
и поле скоростей в области между конусом
и скачком уплотнения; во втором случае
– угол
и поле скоростей, в том числе и величину
скорости на поверхности конуса
.
Для
численного интегрирования систему
дифференциальных уравнений приведем
к безразмерному виду и представим в
виде уравнений в конечных разностях, в
которых
;
;
– приращение угла
;
– угол промежуточного конуса (
).
Величина
при начале расчетов с поверхности скачка
уплотнения определяется как
(при
),
при расчете с поверхности конуса – как
(при
).
Тогда
(9.6)
Рассмотрим
кратко порядок ведения расчета при
интегрировании с поверхности конуса.
Зададимся углом полураствора конуса
и скоростью
на его поверхности. Зададимся приращением
,
т. е. шагом интегрирования. На нулевом
шаге (
)
имеем следующее:
и
.
Делаем
первый шаг по углу
:
.
Из первого уравнения системы (9.6) получаем
,
так как
и
.
Подставим полученное значение
во второе уравнение системы и найдем
на промежуточном конусе с углом
и т. д. Интегрирование проводим до тех
пор, пока не будет выполняться условие
(9.5) на поверхности скачка, также
приведенное к безразмерному виду.
Р
p
за скачком уплотнения и параметры поля
течения между скачком и конусом, используя
формулы изоэнтропического течения.
Найдем коэффициент волнового сопротивления изолированного конуса, отнесенный к площади наибольшего сечения (площади донного среза конуса). Сила лобового сопротивления, действующая на конус (рис. 9.2), равна
,
так
как
.
Поскольку повышенное давление на
поверхности конуса создается за счет
потерь части механической энергии
сверхзвукового потока в скачке уплотнения,
то возникающее за счет этого сопротивление
называют волновым.
Тогда коэффициент сопротивления, он же
коэффициент волнового сопротивления,
равен
. (9.7)
Таким
образом, можно сделать заключение, что
коэффициент
волнового сопротивления изолированного
конуса численно равен коэффициенту
давления на его поверхности
.
Коэффициент
давления на поверхности конуса
рассчитывается по общему выражению для
коэффициента давления:
.
Расчеты показывают, что скорость потока на поверхности конуса меньше, чем за скачком уплотнения, а угол поворота потока при переходе через конический скачок уплотнения меньше угла конуса < . Угол наклона вектора скорости при перемещении от скачка к конусу увеличивается до . Поэтому линии тока в возмущенной области (в отличие от клина) являются криволинейными (рис. 9.3).
Скорость
потока вдоль этих линий уменьшается, а
давление возрастает. Следовательно,
при обтекании конуса поток испытывает
сначала ударное сжатие на скачке
уплотнения, а затем изоэнтропическое
повышение давления (сжатие) в области
между скачком и поверхностью конуса.
Вследствие этого волновые потери
(волновое сопротивление) конуса при
прочих равных условиях (
)
меньше, чем для клина. Угол наклона
конического скачка уплотнения
при одинаковой величине
и
меньше угла наклона плоского косого
скачка уплотнения, а максимальный угол
поворота
,
до которого скачок остается присоединенным,
при этом больше, чем для плоского скачка
уплотнения (рис. 9.4).
Фронт
конического
скачка
уплотнения
Линия тока
Рис. 9.3. Форма скачка уплотнения и линий тока. Изменение давления
и скорости вдоль линии тока
Рис.
9.4. Углы наклона косого
и
конического скачков
уплотнения