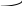3.3. Непрерывная случайная величина. Интегральная функция распределения и ее свойства.

Аналитически закон распределения случайной величины можно задать с помощью ее функции распределения. Отметим, что с помощью функции распределения или интегральной функции распределения можно задать как дискретную, так и непрерывную случайную величину.

Определение. Функцией распределения или интегральной функцией распределения вероятностей называется вероятность того, что случайная величина примет значение меньшее, чем произвольное действительное число , т.е.

. .

Свойства интегральной функции распределения

Свойство 1. Областью определения функции является все множество действительных чисел

.

Доказательство. Свойство следует из определения интегральной функции распределения.

Свойство 2. Областью изменения функции является промежуток от нуля до единицы

Доказательство. Так как по определению интегральная функция – это вероятность события , то по свойствам вероятности

.

Свойство 3. Предел интегральной функции при равен 1, а при равен 0

Доказательство. Из определения интегральной функции распределения следует, что равенство равносильно . Поэтому

.

Так как событие , состоит в том, что случайная величина в результате исхода испытания примет какое-то действительное число, является событием достоверным.

Найдем

.

Так как – это символ, меньше которого не может быть никакое действительное число, то событие , состоящее в том, что случайная величина примет в результате исхода испытаний значение меньшее , является событием невозможным.

Свойство 4. Интегральная функция распределения является неубывающей функцией.

Доказательство. Выберем два действительных произвольных числа и так, чтобы .

Тогда событие можно представить в виде суммы двух несовместимых событий .

Применив теорему сложения для несовместных событий, находим

или с учетом определения интегральной функции распределения имеем

. (1)

Так как , то из равенства (1) получаем равенство

.

Таким образом, доказано, что для любых значений и для которых выполняется неравенство , выполняется неравенство

,

следовательно, функция неубывающая на всей числовой прямой.

Свойство 5. Вероятность того, что случайная величина примет значение из промежутка определяется по формуле

, (2)

т.е. вероятность того, что случайная величина примет значение из промежутка , равна приращению интегральной функции распределения на этом промежутке.

Доказательство. Формула (2) следует из формулы (1).

Прежде, чем сформулировать остальные свойства интегральной функции распределения, уточним определение случайной величины.

Определение. Случайная величина называется непрерывной, если ее интегральная функция распределения непрерывно дифференцируема.

Рассмотрим теперь свойства интегральной функции распределения, которые справедливы лишь для непрерывных случайных величин.

Свойство 6. Если случайная величина непрерывна, то вероятность того, что она примет любое отдельное возможное значение равна нулю

.

Доказательство. По свойству 5 вероятность того, что случайная величина принимает значение из некоторого промежутка , определяется по формуле

(3)

В равенстве (3) перейдем к пределу при , получим (4)

Так как при , с одной стороны, получаем

, (4)

а, с другой стороны, из непрерывности случайной величины следует непрерывность интегральной функции распределения , а поэтому бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции

(6)

Подставляя найденные значения пределов (5) и (6) в равенство (4), получаем

.

Свойство 7. Если случайная величина непрерывна, то имеют место равенства

.

Доказательство. Докажем, например, первое равенство

.

Так как событие можно представить в виде суммы двух несовместимых событий

,

то, применив теорему сложения для двух несовместных событий, находим

.

Остальные равенства доказываются аналогично.

Р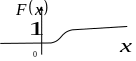 ассмотрим графики интегральной функции распределения.

	а) Если значения непрерывной случайной величины заполняют бесконечный промежуток , то ее график имеет вид изображенный на рисунке 1.
	б) Если все значения непрерывной случайной величины лежат на промежутке , то при , т.к. значения случайной величины, меньшее невозможны, при , т.к. событие при . Следовательно, график интегральной функции в этом случае имеет вид, изображенный на рисунке 2.
	в) График интегральной функции распределения для дискретной случайной величины, заданной таблицей вида … … имеет ступенчатый вид. В точках возможных значений интегральная функция распределения терпит разрыв первого рода, причем в каждой из этих точек она непрерывна слева и имеет разрыв справа. Величина скачка равна вероятности соответствующего значения случайной величины. .

Пример 1. Дискретная случайная величина задана таблицей

	-1	1	3
	0,3	3	0,5

Найти интегральную функцию распределения вероятностей и построить ее график.

Решение. Отметим на числовой прямой возможность значения случайной величины .

При построении интегральной функции распределения рассмотрим случаи:

	, в этом случае , т.к. на интервале не содержится возможных значений ;
		2) , в этом случае
		3) , в этом случае .
		4) , в этом случае .

Таким образом, интегральную функцию распределения можно записать в виде

П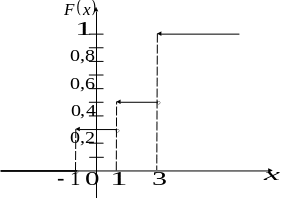 остроим график функции

График функции имеет ступенчатый вид. В точках возможных значений функция имеет разрывы первого рода, причем в каждой из этих точек функция непрерывна слева и имеет разрыв справа. Величина скачка в каждой точке разрыва равна вероятности соответствующего значения случайной величины.