Тема 15. Игры в условиях неопределенности. Критерий принятия решений
Пусть
в игре с природой
П игрок
А обладает
т возможными
чистыми стратегиями
,
а природа П
может находиться в одном из
п состояний
.
Пусть (22.1) является матрицей выигрышей
игрока А.
Обобщенный
критерий пессимизма-оптимизма Гурвица
относительно выигрышей с коэффициентами
.
Переставим
выигрыши
при каждой стратегии
(т. е. элементы каждой строки матрицы
(22.1)), расположив их в неубывающем порядке,
и обозначим элементы полученной матрицы
через
,
а саму матрицу - через В:
B= |
|
1 |
2 |
… |
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
.
(15.1)
Каждая
строка
матрицы В
является перестановкой выигрышей при
стратегии
.
Не исключена возможность, что для
некоторых номеров
и
будет иметь место равенство
.
В силу неравенств (23.1) в первом столбце
матрицы В
стоят минимальные выигрыши при каждой
стратегии
,
(15.2)
а в последнем -м столбце - максимальные выигрыши при каждой стратегии
.
(15.3)
Пусть
числа
удовлетворяют
условиям
и
.
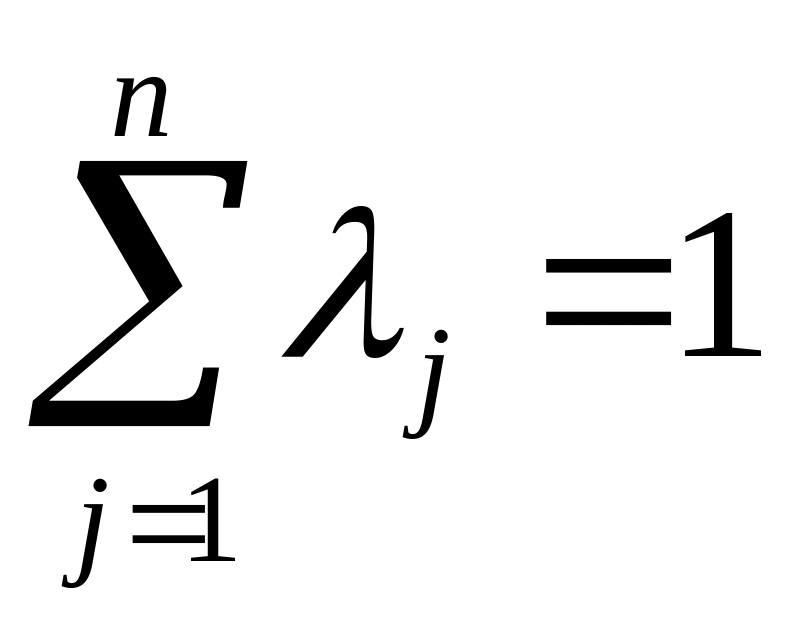(15.4)
Показателем эффективности стратегии по рассматриваемому критерию назовем число
.
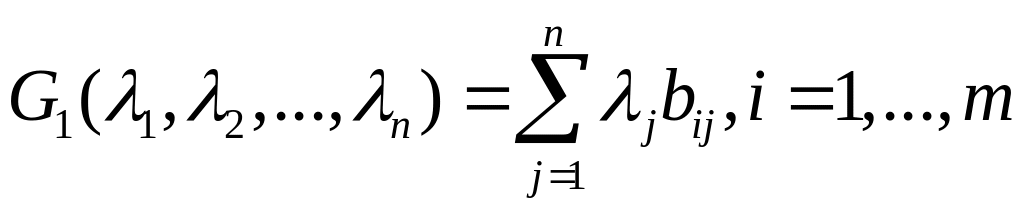(15.5)
Из
этого определения видно, что показатель
эффективности стратегии
учитывает все выигрыши при этой стратегии
и зависит от чисел
,
удовлетворяющих условиям (15.4).
Обобщенным критерием пессимизма-оптимизма Гурвица относительно выигрышей с коэффициентами , назовем критерий, по которому оптимальной среди чистых стратегий считается стратегия с максимальным показателем эффективности (15.5), т.е.
Числа
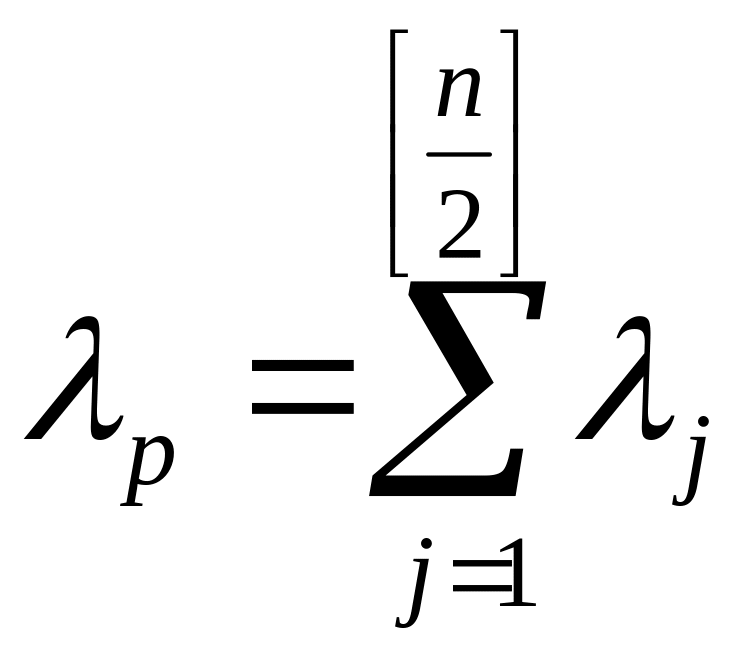и
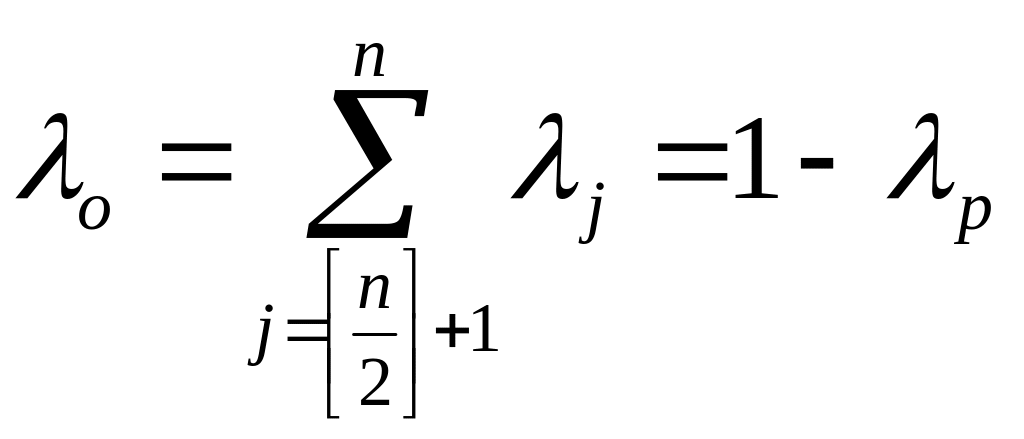(15.6)
назовем
показателями
соответственно
пессимизма
и оптимизма.
В обозначениях
(15.6) индекс
- первая буква английского pessimism,
индекс "о" - первая буква английского
optimism,
а
- целая часть числа
,
т. е. наибольшее целое число, не
превосходящее числа
;
очевидно, что
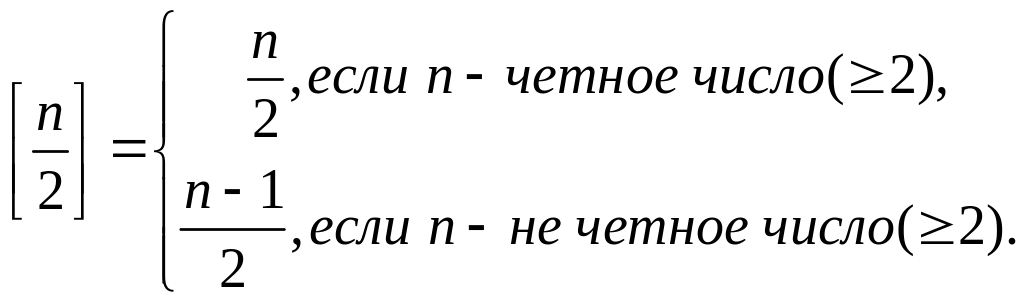
Коэффициенты
выбираются
из субъективных соображений следующим
образом: чем опаснее ситуация, тем больше
возтникает желание в ней
подстраховаться, тем больше, т. е. ближе
к единице, должен быть коэффициент
пессимизма
(см.
(15.6)) и, следовательно, тем меньше, т.е.
ближе к нулю, будет коэффициент оптимизма
.
В безопасной ситуации коэффициенты
выбираются
так, чтобы показатель пессимизма
был ближе к нулю, а показатель оптимизма
- ближе к единице. Таким образом, показатели
пессимизма
и оптимизма
в данном критерии выражают количественную
меру соответственно пессимизма и
оптимизма игрока
А, выбирающего
коэффициенты
.
Если
показатель оптимизма
и, следовательно, показатель пессимизма
,
то критерий - более "оптимистический",
чем "пессимистический"; если,
наоборот, показатель оптимизма
и, следовательно,
показатель пессимизма
,
то критерий - более "пессимистический",
чем "оптимистический"; если же
показатели оптимизма и пессимизма
равны:
,
то критерий можно считать реалистическим.
Критерий Вальда (критерий крайнего пессимизма). Критерий Вальда есть частный случай обобщенного критерия Гурвица относительно выигрышей со специальными коэффициентами
.
(15.7)
которые, очевидно, удовлетворяют условиям (14.4).
Подставляя значения коэффициентов (15.7) в формулу (15.5) и учитывая (15.2), получим показатель эффективности стратегии по критерию Вальда:
.
(15.8)
представляющий собой минимальный выигрыш игрока А при применении им стратегии . Оптимальной среди чистых стратегий по критерию Вальда является, таким образом, стратегия , имеющая максимальный показатель эффективности (15.8):
.
Максимаксный критерий (критерий крайнего оптимизма). Противоположностью критерию Вальда является так называемый максимаксный критерий, представляющий собой также частный случай обобщенного критерия Гурвица относительно выигрышей, когда коэффициенты выбираются следующим образом:
.
(15.9)
Тогда оптимальной среди чистых стратегий по максимаксному критерию является стратегия с максимальным показателем эффективности
,
(15.10)
т.е. стратегия, максимальный выигрыш при которой максимален среди максимальных выигрышей всех чистых стратегий. По-другому можно сказать, что оптимальной будет та чистая стратегия, при которой (хотя бы) один из выигрышей является максимальным среди выигрышей всех чистых стратегий. Оптимальная по максимаксному критерию стратегия гарантирует игроку А возможность наибольшего выигрыша, равного максимаксу
.
Критерий
пессимизма-оптимизма Гурвица относительно
выигрышей с показателем оптимизма
.
Данный критерий является как бы
промежуточным между критериями крайнего
пессимизма и крайнего оптимизма и
представляет собой частный случай
обобщенного критерия Гурвица относительно
выигрышей с коэффициентами
,
удовлетворяющими, очевидно, условиям (15.4).
Оптимальной же стратегией по этому критерию считается стратегия с максимальным показателем эффективности
.
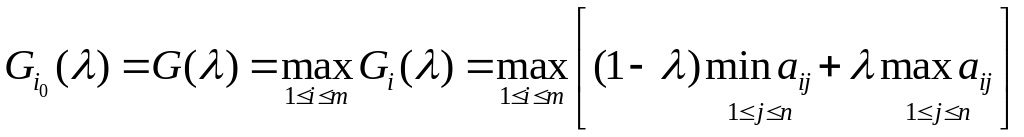