
- •Учебно-методические материалы Теоретический курс Тема 1. Задачи теории игр в экономике Математические модели игр
- •Основные понятия
- •Классификация игр
- •Тема 2. Математические модели игр
- •Тема 3. Антагонистические игры Максиминные и минимаксные стратегии. Нижняя и верхняя цены игры в чистых стратегия
- •Тема 4. Решение антагонистической игры с седловой точкой
- •Тема 5. Смешанные стратегии
- •Тема 6. Функции выигрыша в смешанных стратегиях
- •Тема 7. Решение игры в смешанных стратегиях
- •Тема 8. Критерии и свойства оптимальных стратегий
- •Тема 9. Принцип доминирования
- •Тема 10. Игры 2хп
- •Тема 11. Игры
- •Тема 12. Игры и их решение с помощью линейного программирования
- •Тема 13. Игры в условиях риска
- •Тема 14. Принятие решение в условиях риска на основе модели игры с природой
- •Тема 15. Игры в условиях неопределенности. Критерий принятия решений
- •Тема 16. Позиционные игры Понятие позиционной игры и ее нормальной формы
- •Графическое представление позиционной игры
- •Определение позиционной игры
- •Позиционные игры с полной информацией
- •Позиционные игры с идеальной памятью
Тема 11. Игры
В
этом параграфе рассмотрим игру
,
в которой игрок
обладает
чистыми стратегиями
,
а игрок
![]() -
двумя чистыми стратегиями
и
.
Матрица игры имеет вид
-
двумя чистыми стратегиями
и
.
Матрица игры имеет вид
A= |
|
|
|
|
|
|
|
|
|
|
|
… |
… |
… |
|
|
|
|
Известно,
что показатель неэффективности
![]() стратегии
стратегии
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
игрока
имеет вид
,
игрока
имеет вид
![]() .
.
Если
обозначить
![]() ,
то
,
то
![]() и
и
![]() .
(11.1)
.
(11.1)
Таким
образом, показатель неэффективности
![]() стратегии
стратегии
![]() есть верхняя
огибающая
линейных функций
есть верхняя
огибающая
линейных функций
![]() ,
,
![]() зависящих от вероятности
зависящих от вероятности
![]() ,
график каждой из которых представляет
собой отрезок определенного наклона в
зависимости от знака углового коэффициента
,
график каждой из которых представляет
собой отрезок определенного наклона в
зависимости от знака углового коэффициента
![]() этой функции.
этой функции.
Если
стратегия
![]() удовлетворяет равенству
удовлетворяет равенству
![]() (11.2)
(11.2)
где
![]() — множество всех смешанных стратегий
игрока В,
то по основной теореме фон Неймана она
является оптимальной. Таким образом,
абсцисса
— множество всех смешанных стратегий
игрока В,
то по основной теореме фон Неймана она
является оптимальной. Таким образом,
абсцисса
![]() минимальной (наинизшей) точки верхней
огибающей
определяет оптимальную стратегию
,по
которой игрок В случайным образом
выбирает свои чистые стратегии
с вероятностью
минимальной (наинизшей) точки верхней
огибающей
определяет оптимальную стратегию
,по
которой игрок В случайным образом
выбирает свои чистые стратегии
с вероятностью
![]() и
с вероятностью
и
с вероятностью
![]() .
.
По той же теореме фон Неймана цена игры
![]() ,
(11.3)
,
(11.3)
т. е. цена игры V равна ординате минимальной точки верхней огибающей.
Из сказанного легко сформулировать алгоритм "В" геометрического нахождения оптимальных стратегий игрока В и цены игры V(см. рис. 17.1).
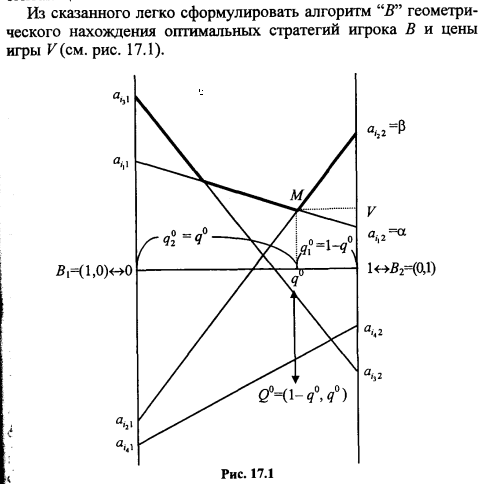
Рис. 11.1
Алгоритм "В"
Берем горизонтальный отрезок [0,1].
Через концы отрезка [0,1] проводим к нему два перпендикуляра: левый и правый.
На левом перпендикуляре, лежащем на вертикальной числовой оси, от точки 0 его пересечения с отрезком [0,1] откладываем все элементы первого столбца матрицы А.
На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все элементы второго столбца матрицы А.
Каждую пару точек, изображающих элементы
 и
и
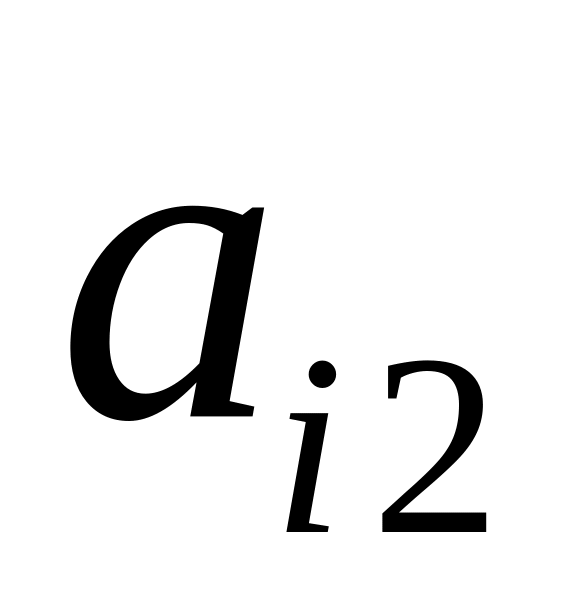 ,
стоящие
в
,
стоящие
в
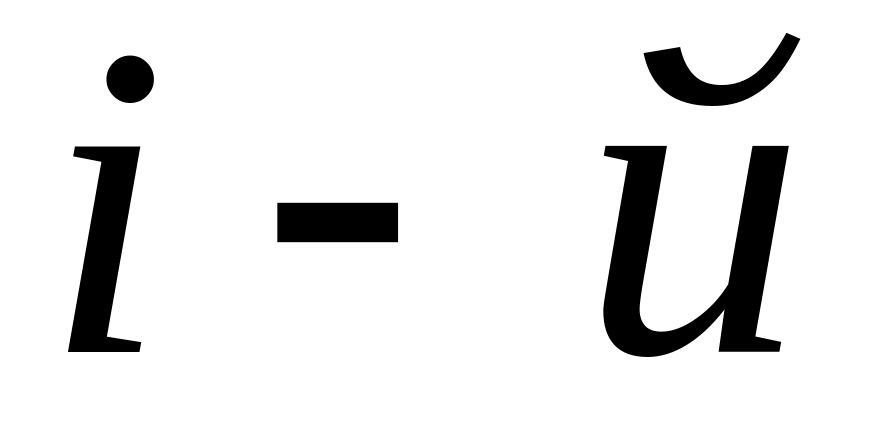 строке матрицы А, соединяем отрезком
строке матрицы А, соединяем отрезком
 в результате чего построим
отрезков, представляющих собой графики
линейных функций
в результате чего построим
отрезков, представляющих собой графики
линейных функций
![]() (11.4)
(11.4)
Если все отрезки
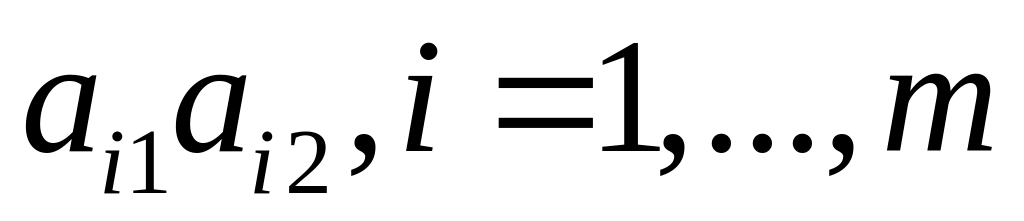 ,
имеют неотрицательный наклон, т. е.
положительный или нулевой (другими
словами, все отрезки
,
имеют неотрицательный наклон, т. е.
положительный или нулевой (другими
словами, все отрезки
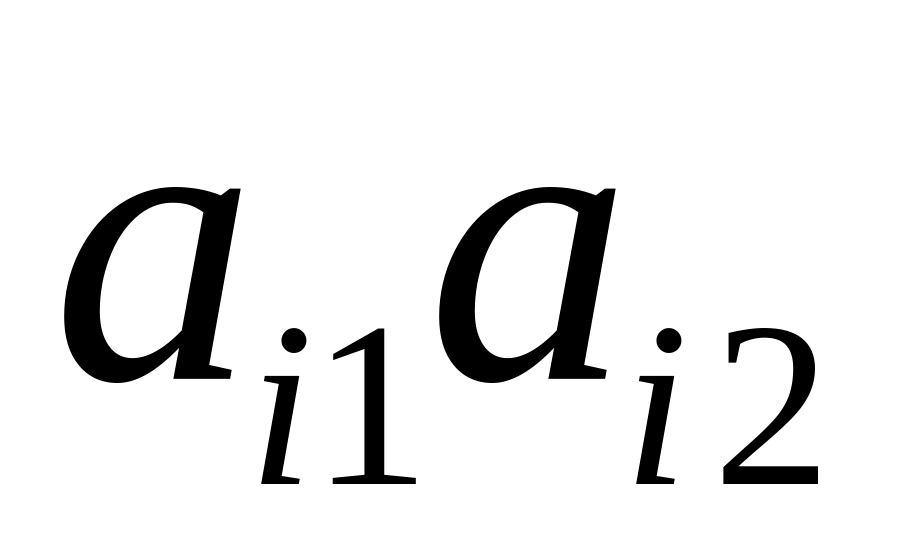 - неубывающие:
- неубывающие:
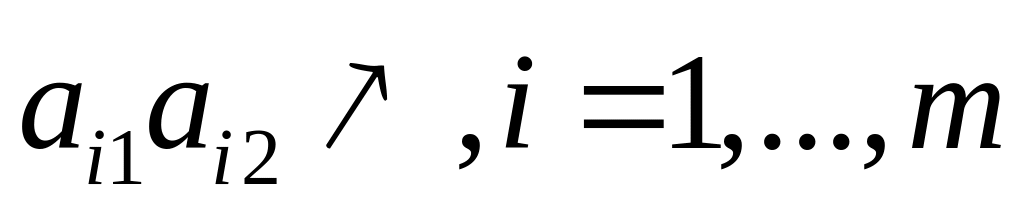 ,
то стратегия
,
доминирует стратегию
.
Если все отрезки
,
имеют положительный наклон, т. е. являются
возрастающими:
,
то стратегия
,
доминирует стратегию
.
Если все отрезки
,
имеют положительный наклон, т. е. являются
возрастающими:
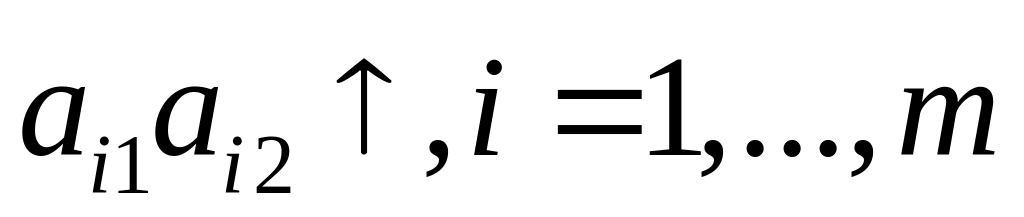 ,
то стратегия
строго доминирует стратегию
.
,
то стратегия
строго доминирует стратегию
.Если все отрезки , имеют неположительный наклон, т. е. отрицательный или нулевой (другими словами, все отрезки , - невозрастающие:
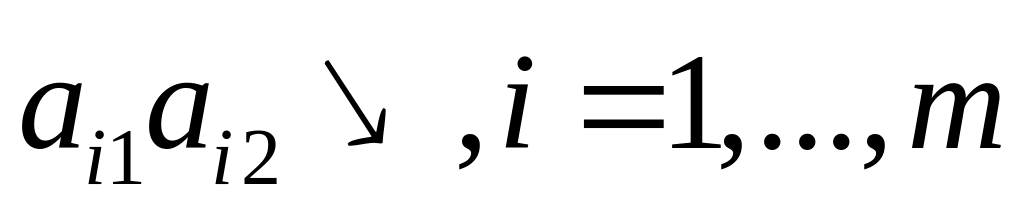 ,
то стратегия
доминирует стратегию
.
Если все отрезки
,
имеют отрицательный наклон, т. е. являются
убывающими:
,
то стратегия
доминирует стратегию
.
Если все отрезки
,
имеют отрицательный наклон, т. е. являются
убывающими:
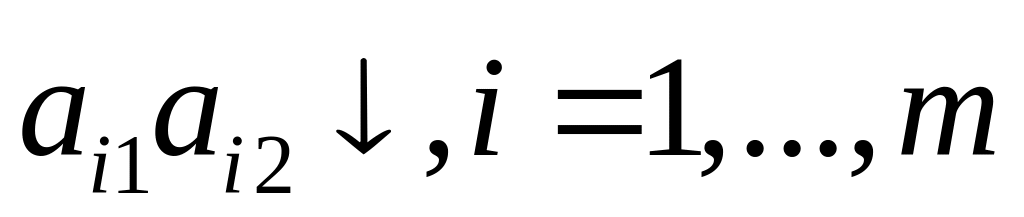 ,
то стратегия
строго доминирует стратегию
.
,
то стратегия
строго доминирует стратегию
.Отрезок
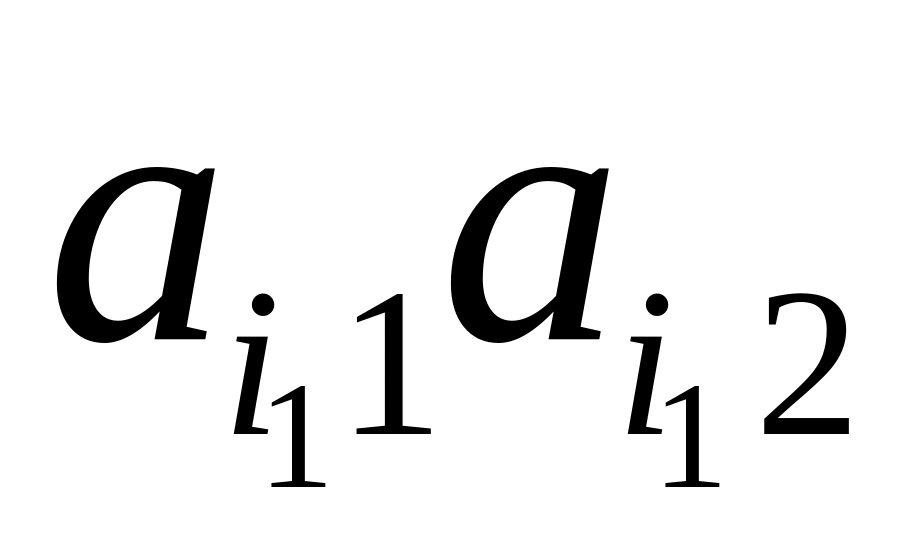 лежит не ниже отрезка
лежит не ниже отрезка
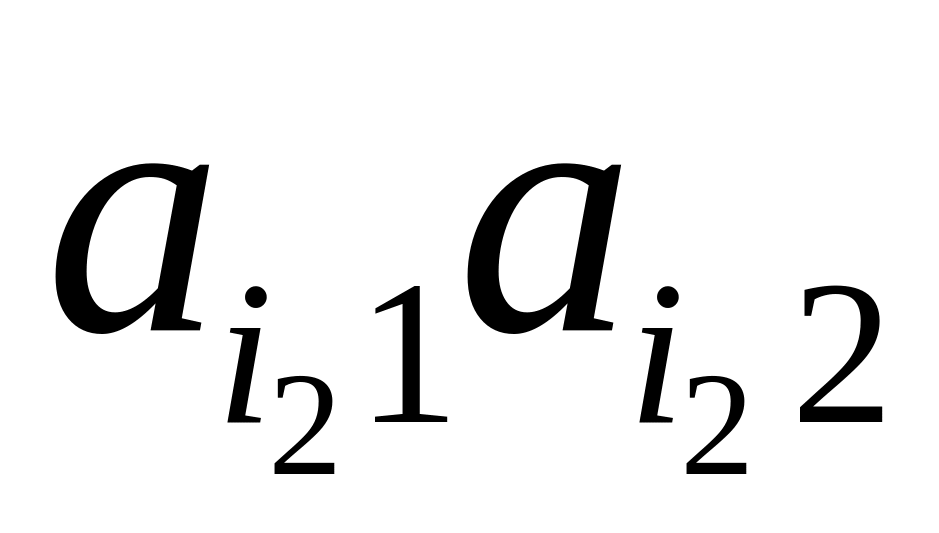 ,
,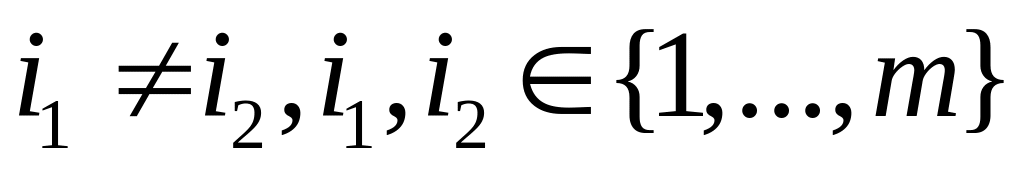 ,
то стратегия
,
то стратегия
 доминирует стратегию
доминирует стратегию
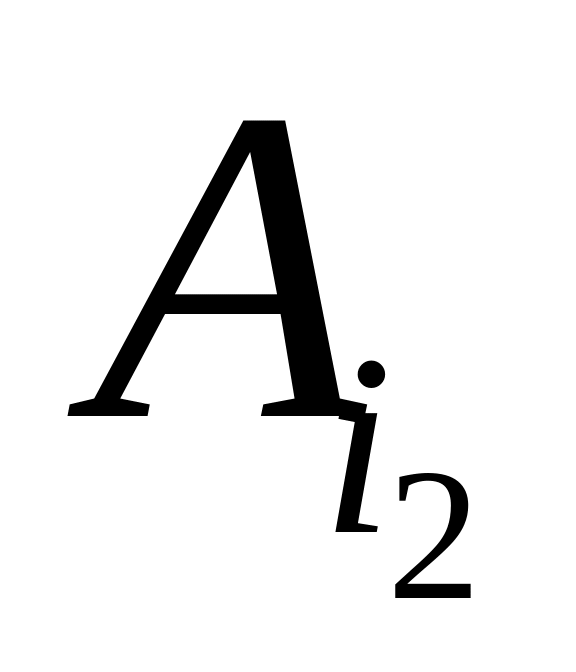 .
Если отрезок
лежит выше отрезка
,
,
то стратегия
строго доминирует стратегию
.
.
Если отрезок
лежит выше отрезка
,
,
то стратегия
строго доминирует стратегию
.Находим (выделяем) верхнюю огибающую (17.1) семейства отрезков (17.4), представляющую собой в общем случае выпуклую вниз ломаную, которая, в частности, может быть и отрезком.
На верхней огибающей находим минимальную (наинизшую) точку (точки).
Абсцисса минимальной точки (удовлетворяющая равенству (17.2)) является вероятностью случайного выбора игроком В чистой стратегии В2 в оптимальной смешанной стратегии .
Ордината минимальной точки верхней огибающей является ценой игры
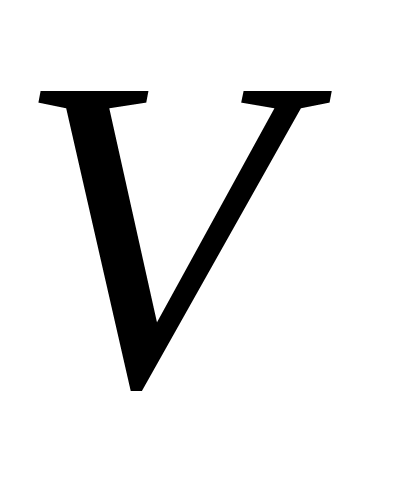 (см. (17.3)).
(см. (17.3)).Верхний из нижних концов отрезков , является нижней ценой игры в чистых стратегиях .
Нижний из концов верхней огибающей (лежащих на перпендикулярах) является верхней ценой игры в чистых стратегиях .
Элемент матрицы А, представленный на рисунке точкой являющейся нижним концом отрезка, на котором она лежит, и верхним на перпендикуляре, которому она принадлежит, является седловой точкой игры. В этом случае чистая стратегия игрока А, номер которой совпадает с первым индексом седловой точки, является оптимальной.
На
рис. 17.1 из
т
отрезков
,
указаны четыре
![]() ,
первые три из которых принимают участие
в конструировании верхней огибающей,
выделенной" жирной линией. Точка М -
минимальная точка этой верхней огибающей,
имеющая своей абсциссой
.
Поэтому
- оптимальная смешанная стратегия игрока
В.
Ордината точки
М есть
цена игры
V.
Нижняя цена игры в чистых стратегиях
,
первые три из которых принимают участие
в конструировании верхней огибающей,
выделенной" жирной линией. Точка М -
минимальная точка этой верхней огибающей,
имеющая своей абсциссой
.
Поэтому
- оптимальная смешанная стратегия игрока
В.
Ордината точки
М есть
цена игры
V.
Нижняя цена игры в чистых стратегиях
![]() ,
верхняя цена игры в чистых стратегиях
,
верхняя цена игры в чистых стратегиях
![]() .
Так как среди отрезков
-
имеются отрезки с положительным и
отрицательным наклонами (например,
отрезок
имеет положительный наклон, а отрезок
.
Так как среди отрезков
-
имеются отрезки с положительным и
отрицательным наклонами (например,
отрезок
имеет положительный наклон, а отрезок
![]() - отрицательный), то стратегия
В2
не доминирует и не доминируется стратегией
.
Так как отрезки
и
лежат выше отрезка
- отрицательный), то стратегия
В2
не доминирует и не доминируется стратегией
.
Так как отрезки
и
лежат выше отрезка
![]() ,
то каждая из стратегий
и
строго доминирует стратегию
,
то каждая из стратегий
и
строго доминирует стратегию
![]() .
Оптимальную стратегию
игрока
В и
цену игры
V можно
подсчитать и по формулам, которые даются
в следующей теореме.
.
Оптимальную стратегию
игрока
В и
цену игры
V можно
подсчитать и по формулам, которые даются
в следующей теореме.
Теорема
11.1.
Если через минимальную точку М верхней
огибающей отрезков
,
порождаемых чистыми стратегиями
,![]() ,
игрока
А, проходят два каких-либо отрезка
и
,
,
то абсцисса точки М
,
игрока
А, проходят два каких-либо отрезка
и
,
,
то абсцисса точки М
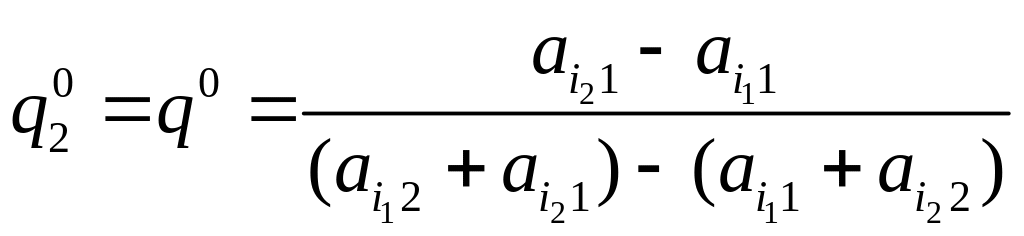
и, следовательно,
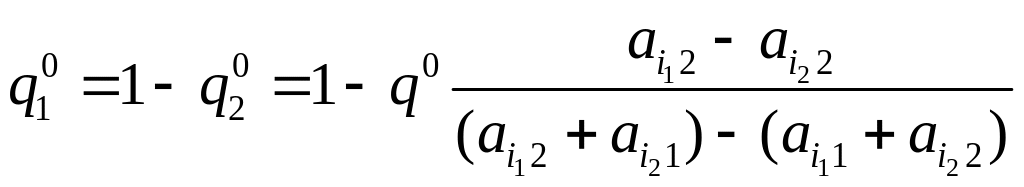 ,
,
а цена игры
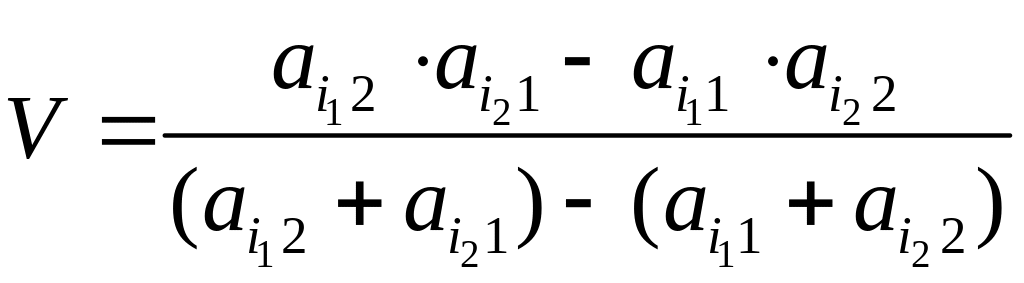 .
.
Теорема 11.2. Пусть через минимальную точку М верхней огибающей отрезков , порождаемых чистыми стратегиями А , , игрока А, проходят два каких-либо отрезка и , .
Для того чтобы смешанная стратегия игрока А, где
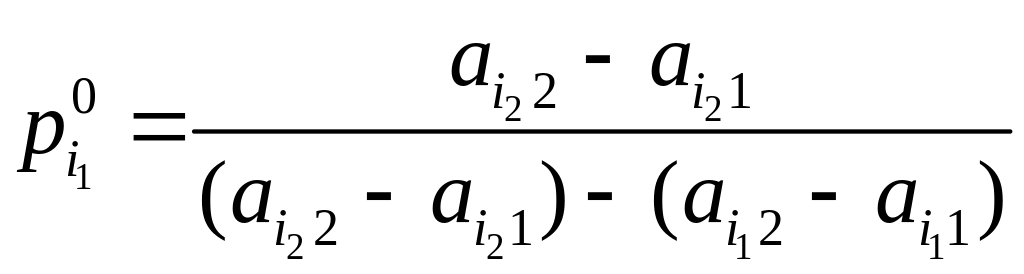 ,
,
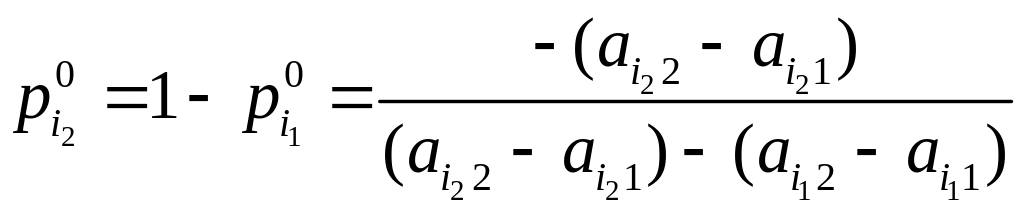
![]()
была оптимальной,
необходимо и достаточно, чтобы отрезки
и
![]() ,
имели разные
наклоны.
,
имели разные
наклоны.
