
4.3. Визначники
Визначником п-го порядку квадратної числової матриці А порядку п називають число, яке знаходиться з елементів матриці А як суму добутків по одному числу з кожного рядка і кожного стовпця. Визначник матриці А позначають |А| або (А).
Правило знаходження визначника 2 порядку: визначник другого порядку дорівнює різниці добутків елементів головної та допоміжної діагоналей, тобто
![]() (1)
(1)
Схему цієї формули можна зобразити таким чином
“-“
“+”



![]()
a21 a22
Знак (+) вказує, що добуток елементів головної діагоналі треба брати зі своїм знаком, знак (- ) означає, що добуток елементів неголовної діагоналі треба брати з протилежним знаком.
Приклад 1. Обчислити визначники
![]()
Розв'язування. Будемо обчислювати задані визначники за формулою (І):
![]()
![]()
Правило знаходження визначника 3-го порядку: Визначник третього порядку знаходять за формулою
 (2)
(2)
Кожен доданок у правій частині (2) має 3 множники з різних рядків та стовпців. Три перших доданка із знаком (+) є добутками елементів головної діагоналі і елементів вершин трикутників з основами паралельними головній діагоналі (дивись схему а) малюнка 1). Три останні доданки у правій частині (2) мають від'ємний знак. Вони є добутками елементів неголовної діагоналі та елементів вершин трикутників із основами паралельними неголовній діагоналі (рис. 1 b).

Рис. 1
Ця схема обчислення визначника третього порядку називається правилом Саріуса. Існують також інші схеми обчислення визначника 3-го порядку.
Приклад
2. Обчислити визначник

Розв'язування. Згідно з формулою (2) одержимо

Для обчислення визначників порядку п > 3 використовують алгебраїчні доповнення.
Означення 1. Мінором Мij елемента аij визначника п-го порядку називається визначник (п- 1) порядку, який одержуємо з визначника | А | шляхом викреслювання і-го рядка та j-го стовпця, на перетині яких знаходиться елемент аij.
Означення 2. Алгебраїчним доповненням Аij елемента аij визначника називають мінор цього елемента, взятий зі знаком (-1)i+j, тобто
Aij=(-1)i+j Mij (3)
Приклад 3. Знайти алгебраїчні доповнення до елементів a21 та a33
визначника
 .
.
Розв'язування. Алгебраїчні доповнення до елементів а21 та a33 позначимо А21 та А33, відповідно. Згідно з означенням 2
A21=(-1)2+1M21=-M21; A33=(-1)3+3M33=M33 (4)

 Мінори
М21
та
М33
знайдемо згідно з означенням 1:
Мінори
М21
та
М33
знайдемо згідно з означенням 1:





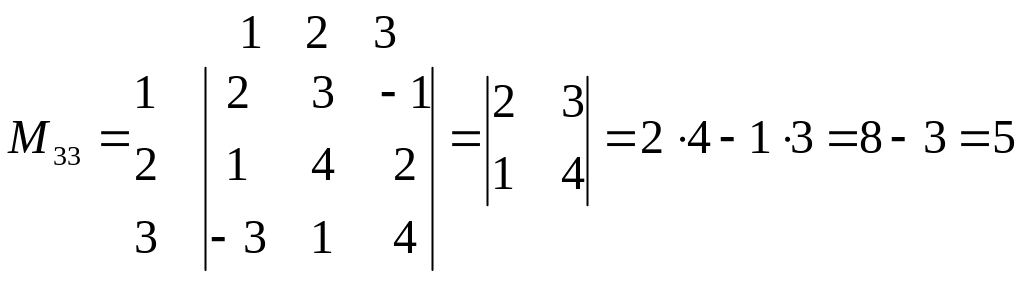


Підставимо ці значення мінорів у відповідні рівності (4), одержимо шукані алгебраїчні доповнення: A21=-13; A33=5.
Тепер можемо сформулювати правило обчислення визначника п-го порядку.
Правило. Визначник п-го порядку дорівнює сумі добутків усіх елементів будь-якого стовпця (або рядка) на відповідні їм алгебраїчні доповнення.
У випадку використання і-го рядка це правило математично
можна записати так
 (5)
(5)
Рівність (5) називають розкладом визначника за елементами і-го рядка. Визначник можна розкласти і за елементами k-го стовпця (k= 1, 2, ..., n).
Отже, обчислення визначника п-го порядку зводиться до обчислення визначників (n - 1) порядку шляхом розкладення визначника за елементами будь-якого рядка або стовпця.
Зауваження. Для скорочення обчислень визначника доцільно його розкласти за елементами такого рядка чи стовпця, який містить найбільшу кількість нулів. У такому випадку не треба знаходити алгебраїчні доповнення до елементів, що дорівнюють 0 (добуток 0 на будь-яке алгебраїчне доповнення дорівнює нулеві).
Таким чином, для ефективного використання методу обчислення визначника шляхом його розкладання за елементами будь-якого рядка або стовпця треба навчитись робити еквівалентні перетворення визначника, які дають можливість одержати нулі у деякому рядку або стовпці.
Виконання таких перетворень здійснюється з використанням деяких властивостей визначника.
Властивості визначників:
1. Визначник при транспонуванні не змінюється.
Пояснення дамо на прикладі визначників другого порядку. Нехай
![]() .
.
Праві частини рівні, тому і ліві також рівні, тобто (А) = (АT).
Наслідок. У визначнику рядки та стовпці мають однакові властивості.
2. Якщо у визначнику поміняти місцями будь-які два рядки (стовпці), то визначник змінить знак на протилежний. Дійсно, якщо у визначнику А поміняти місцями перший і другий рядки, то одержимо
![]()
Наприклад,
![]() ,
тому
,
тому
![]()
3. Якщо визначник має два однакових рядки (стовпця), то він дорівнює нулю.
Дійсно, якщо ми поміняємо місцями рівні рядки (стовпці), то визначник не зміниться, але згідно властивості 2 він повинен змінити знак на протилежний. Тому визначник повинен дорівнювати 0.
Наприклад:
![]() =-6+6=0.
=-6+6=0.
4. Якщо у визначнику усі елементи одного рядка (стовпця) помножити на однакове дійсне число k, то визначник зросте також в k разів.
Наприклад,
(А)=![]() =4-15=-11
=4-15=-11
(А1)=![]() =4k-15k=-11k
=4k-15k=-11k
тобто (А1) =k(A), але |A1 одержано з визначника |А| шляхом множення усіх елементів першого рядка на k.
Наслідок 1. Спільний множник усіх елементів будь-якого рядка (стовпця) визначника можна винести за знак визначника.
Наслідок 2. Якщо усі елементи будь-якого рядка (стовпця) визначника дорівнюють нулю, то визначник дорівнює нулю.
5. Визначник, у якого відповідні елементи двох будь-яких рядків (стовпців) пропорційні, дорівнює нулю. Доведення цієї властивості випливає з властивостей 3 та 4.
6. Якщо у визначнику елементи і-го рядка (k-го стовпця) є сумою двох доданків, тоді він дорівнює сумі двох відповідних визначників.
Наприклад,
 .
.
7. Якщо до всіх елементів будь-якого рядка (стовпця) визначника додати відповідні елементи іншого рядка (стовпця) цього визначника, помножені на одне й те ж саме число, то визначник не зміниться.
Приклад
4.
Нехай заданий визначник
 .
.
Перетворимо визначник таким чином:
1) елементи першого рядка визначника помножимо на (-3) та додамо до відповідних елементів другого рядка визначника;
2) елементи першого рядка визначника помножимо на (-2) та додамо до відповідних елементів третього рядка визначника .
Отримаємо
визначник, який позначимо
через
![]() :
:
 .
.
Перевіримо, що 1= . Для цього обчислимо ці визначники

 .
.
Отже, цей приклад ілюструє:
1) справедливість властивості 7;
2) цю властивість доцільно застосувати до перетворення визначників 4-го та вищих порядків, щоб одержати чим більше нулів у якомусь стовпці (або рядку) і тим самим спростити обчислення заданого визначника.
Приклад 5. Обчислити визначник 4-го порядку
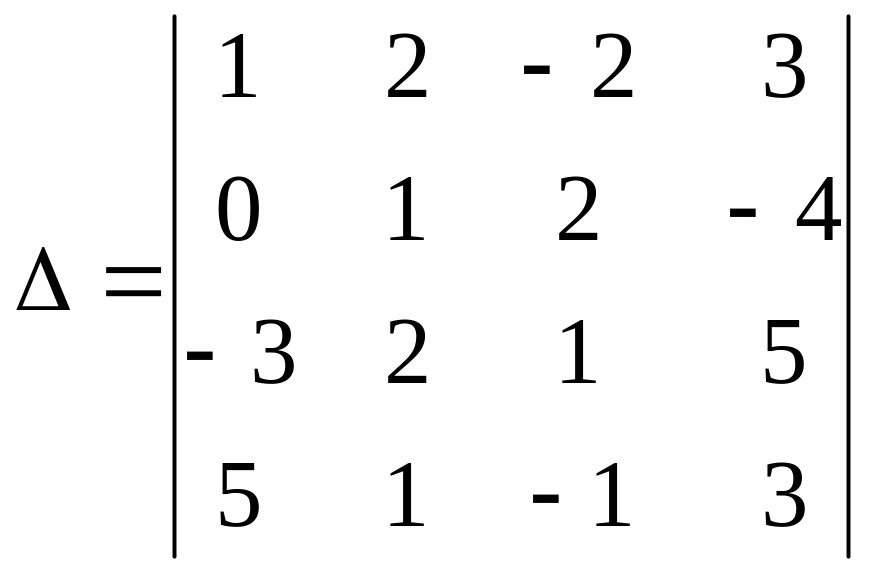
Розв'язування. Перетворимо цей визначник таким чином, щоб зробити якомога більше нулів у якомусь стовпчику, краще у першому, бо там вже є один нуль. Для цього елементи першого рядка помножимо на 3 та додамо до відповідних елементів третього рядка, потім елементи першого рядка помножимо на (-5) та додамо до відповідних елементів четвертого рядка. Одержимо визначник:
 .
.
Тепер визначник доцільно розкласти за елементами першого стовпця:
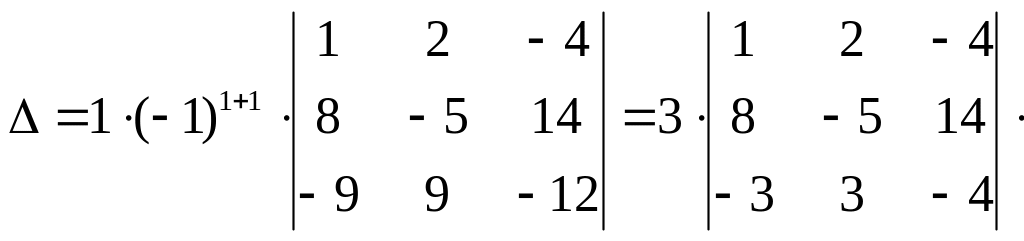
Тут ми використали наслідок 1 властивості 4 і спростили визначник. Обчислимо його:
=3(20-96-84+60-42+64)=3(-78)=-234.
Вправи до розділу 4.3
Обчислити визначники:
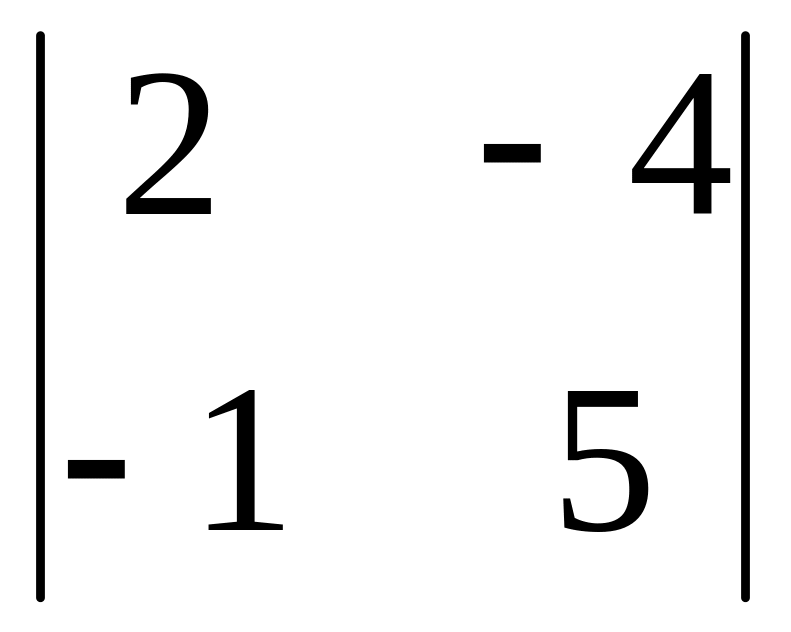 2.
2.
 3.
3.
 4.
4.

 6.
6.
 7.
7.
 8.
8.

 10.
10.
 11.
11.
 12.
12.

 14.
14.
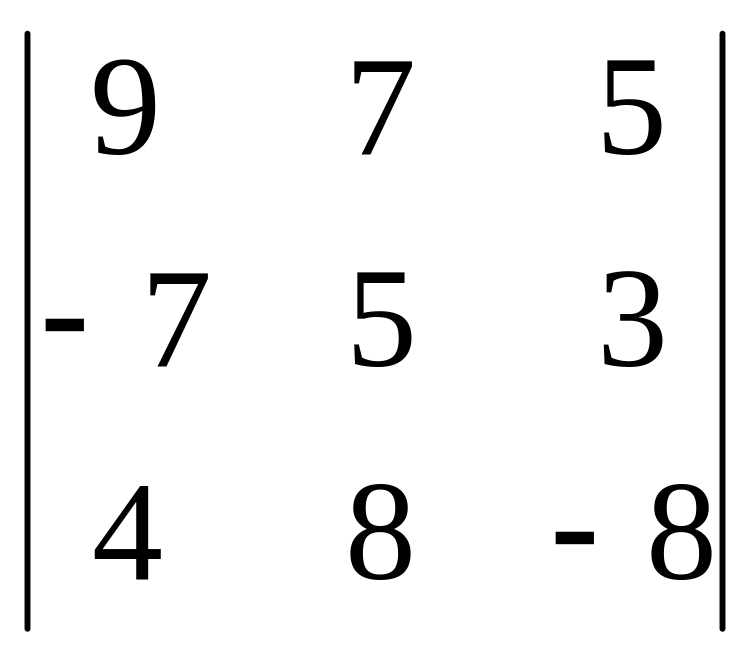 15.
15.
 16.
16.

17.
 18.
18.
 19.
19.
 20.
20.
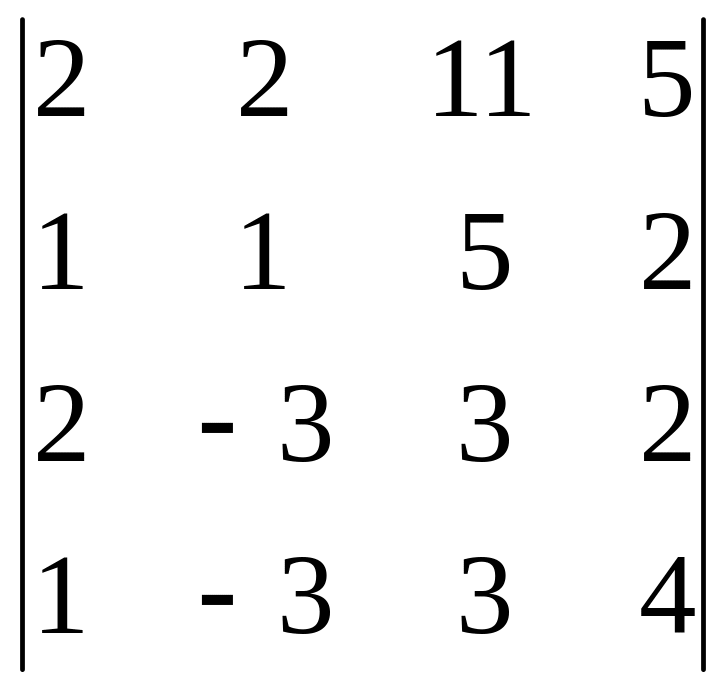
21.
 22.
22.
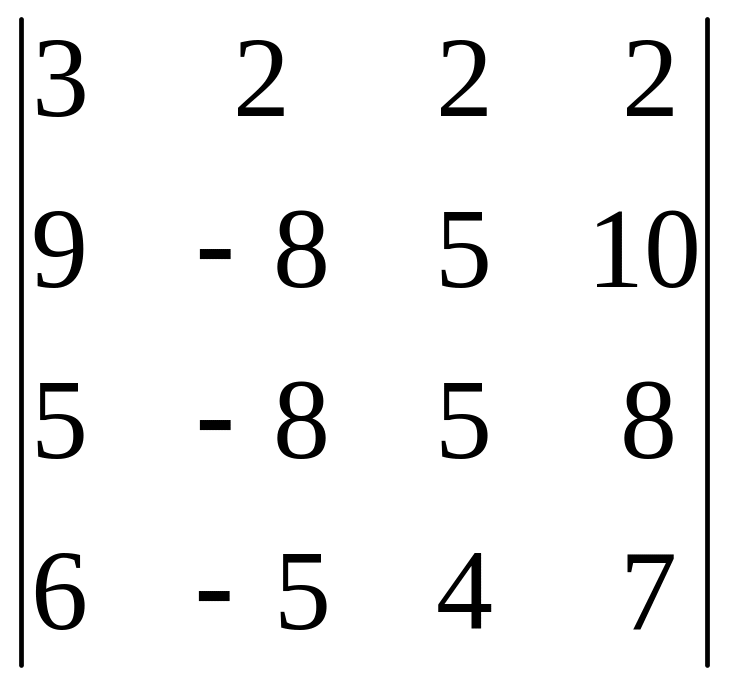 23.
23.
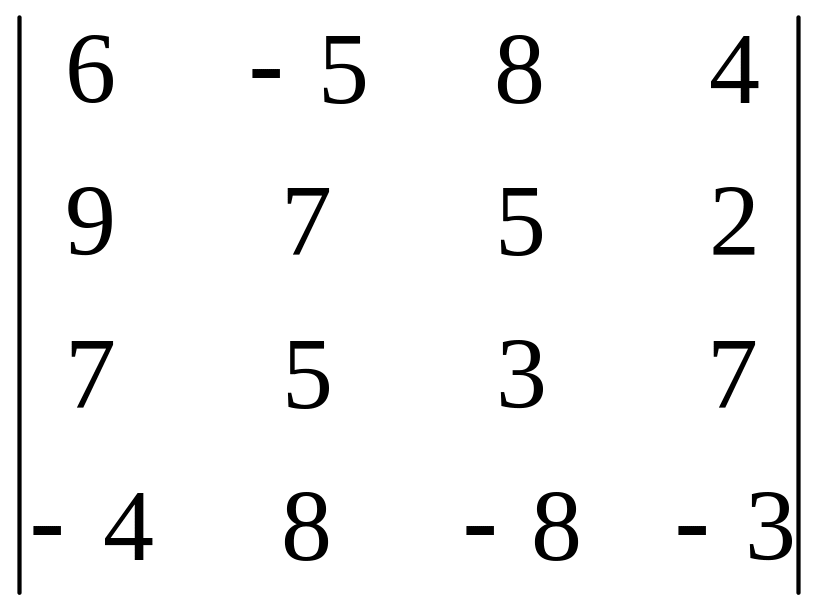 24.
24.

