4. Матриці та визначники

4.1. Різновиди матриць

Означення 1. Матрицею називають таблицю упорядкованих чи­сел або будь-яких інших об'єктів, розташованих в m рядках та n стовпцях.

Матриці позначають великими літерами, наприклад А, В, С... та круглими дужками.

Матриця, яка має m рядків та n стовпців, називається матри­цею розміру m x n (перший множник завжди вказує кількість ряд­ків). Така матриця має вигляд

.

Кожен елемент а_ij матриці А має два індекси: перший індекс і вказує номер рядка, в якому знаходиться цей елемент, другий індекс j вказує номер стовпця, який містить цей елемент. Так, елемент а₂₃„ знаходиться на перетину другого рядка та третього стовпця матриці А.

Матриця розміру m x 1 називається матрицєю-стовпцем або вектором-стовпцем. Матриця розміру 1 x n називається матрицєю-рядком або вектором-рядком.

Наприклад, нехай задані матриці

; ; ; .

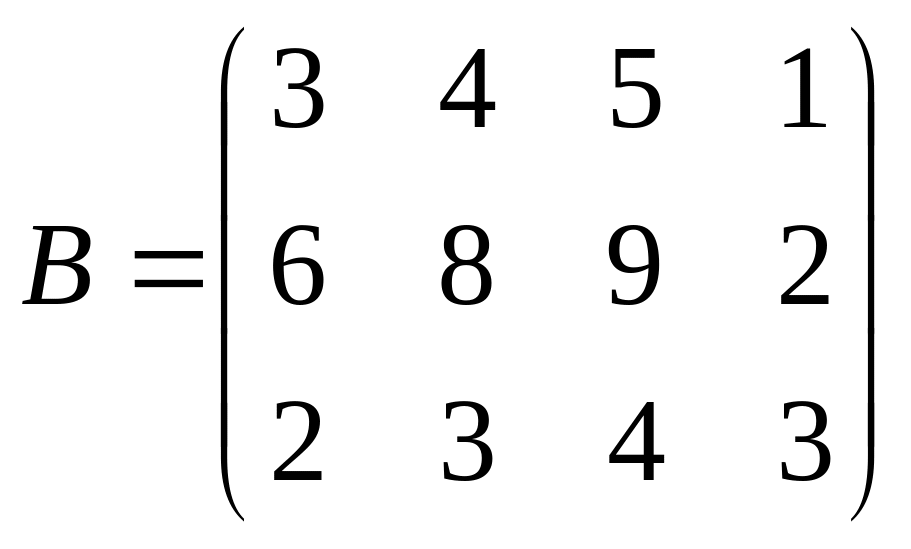Матриця А має розмір 2х3, матриця В розміру 3х4, С — матриця-стовпець розміру 4 x 1, D – матриця-рядок 1х4.

Матрицю називають квадратною порядку n, якщо кількість її рядків однакова з кількістю стовпців і дорівнює n. Наприклад, квадратна матриця А порядку n має вигляд

.

Множина елементів a₁₁, a₂₂, a₃₃,..., a_nn квадратної матриці А порядку n утворюють головну діагональ матриці, а множина елементів a_1n, a_2(n-1), a_3(n-2),..., a_n1 утворює допоміжну (або неголов­ну) діагональ матриці.

Квадратна матриця, у якій а_ij0 лише при i=j називається діагональною. Діагональна матриця з елементами називаєт­ься одиничною матрицею і найчастіше позначається Е або I.

Наприклад, нехай задані матриці

; ; .

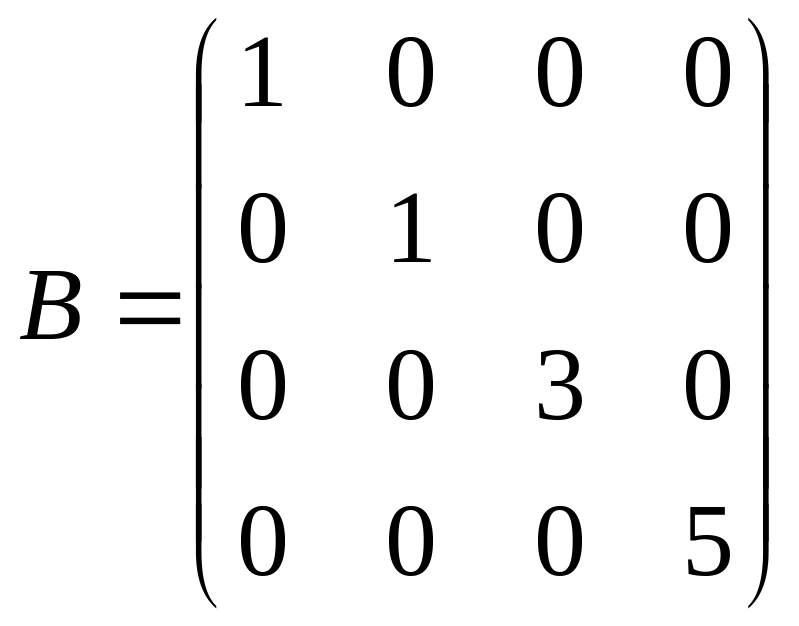В – діагональна матриця 4-го порядку, Е – одинична матри­ця порядку 3, 0 – нульова квадратна матриця порядку 3.

Для скорочення матриці можна записати у вигляді , коли розмір матриці А відомий, або .

Матриці А та В називаються рівними, якщо:

1) вони мають однаковий розмір та

2. їх відповідні елементи рівні, тобто для усіх і=1,2, ...,m;

j= 1, 2 ,..., n.

Якщо в матриці А рядки записати стовпцями із збереженням їх порядку, то одержана матриця називається транспонованою і позначається А^T, а вказана операція перетворення матриці А на­зивається транспонуванням матриці А.

Наприклад,

якщо 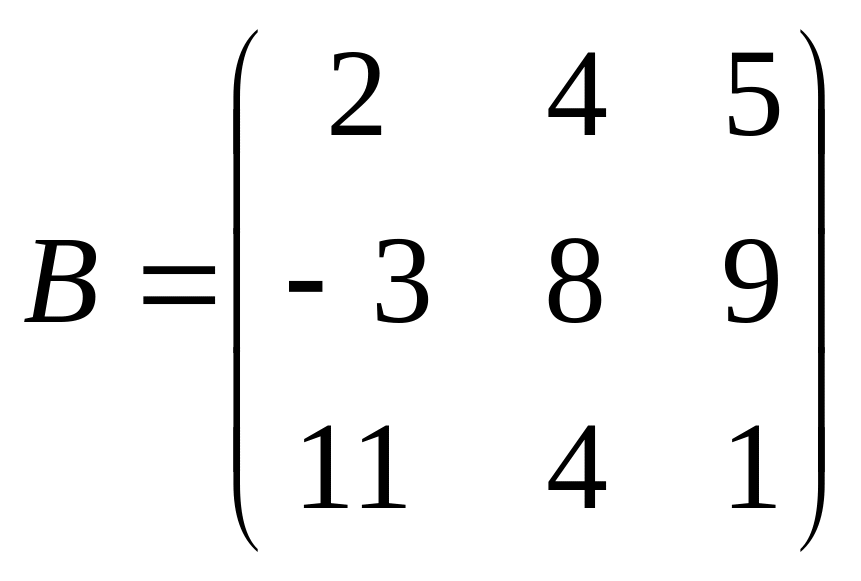, тоді .

Матриці широко використовуються в плануванні виробництва та транспортних перевезень. Вони дозволяють розробляти різні варіанти плану, полегшують дослідження залежності між різни­ми економічними показниками.

Приклад 1. Мале підприємство виробляє 4 види продукції А, В, С та D, використовуючи на кожну з них різну кількість двох матеріалів та праці (кількості робочих годин). Конкрет­на інформація вказана у таблиці

Вироби:	A	B	C	D
Одиниць матеріалу X	250	300	170	200
Одиниць матеріалу Y	160	230	75	0
Кількість робочих годин	80	85	120	100

У цієї ситуації є 12 дійсних чисел, які можна впорядкувати і записати у вигляді матриці

розміру 3х4. Кожен рядок та кожен стовпець цієї матриці має певний зміст. Наприклад, елементи другого рядка вказують кількість витраченого матеріалу Y на виробництво продукції А, В, С та D; елементи другого стовпця матриці вказують кількість витрачених матеріалів X, Y та робочих годин на вироб­ництво продукції В.