
Министерство образования и науки Российской Федерации
Уфимский Государственный Авиационный Технический Университет
Кафедра информатики
Пояснительная записка
к курсовой работе
«Решение систем линейных уравнений»
Тема 2, Вариант 1
Выполнил:
студент гр. Т18-201
Зеленцов А.А
Проверил:
Сираева Л.П.
Уфа – 2005
Содержание:
1.Задание
2. Введение
3. Теория
4. Блок-схем метода Гаусса
5. Описание программы
7. Формы
8. Код программы
9. Заключение
10. Список использованной литературы
Введение
Сейчас в руках вы держите пояснительную записку к программе для расчета линейных уравнений.
Программа выполнена в Visual Basic.
В пояснительной записке объясняется метод решения (а именно метод Гаусса), показана схеме программы, рассказывается каким образом действует программа, представлены графические изображения различных компонентов Visual Basicа, а так же код самой программы.
Теория
Метод Гаусса
С помощью этого метода решают неоднородную систему n линейных алгебраических уравнений с n неизвестными:
a11x1 + a12x2 + ... +a1n xn = a1n+1
a21 x1 + a22 x2 + ... +a2n xn = a2n+1
....
an1 x1 + an2 x2 + ... +ann xn = ann+1
Вначале находим отличный от нуля коэффициент при x1 . Соответствующее уравнение переставляем с первым (если это необходимо!!!). Получаем систему с a11 отличным от нуля. Разделив коэффициенты этого уравнения на a11 , получим:
x1 + b12 x2 + ... + b1n xn = b1n+1
При помощи этого уравнения исключаем x1 из исходной системы:
a (1)22 x2 + a (1)23 x3 + ... + a (1)2n xn = a (1)2n+1
....
a (1)n2 x2 + a (1)n3 x3 + ... + a (1)nn xn = a (1)nn+1
где
a (1)ij = aij - ai1 b1j , i,j= 2...n
и Т.Д.
Полученная система содержит n-1 уравнение. Применяем описанную выше процедуру к этой системе. Операции повторяем требуемое число раз, пока не приведем систему к треугольному виду:
x1 + с12 x2 + ... + с1n xn = с1n+1
x2 + ... + c2n xn = c2n+1
....
xn = cnn+1
Теперь легко определить xn , xn-1 , ..., x1 .
Если при поиске отличного от нуля коэффициента такого не окажется, то матрица системы вырождена и алгоритм неприменим. Для сравнения с нолем в алгоритм передается малое число epsilon, и любое число, по модулю меньшее epsilon, считается нолем. В случае вырожденой матрицы функция возвращает False. Если матрица невырождена, то функция возвращает True, а переменная X содержит решение системы.
Блок-схем метода Гаусса


Описание программы
Эта программа создана, как многооконное приложение, основой которого служит MDI форма. В MDI-форме располагаются следующие формы:
«Файл»
«Система линейных уравнений»
«Визуализация»
«Окно»
«Справка»
Данные о нашем линейном уравнении мы находим в текстовом файле. Далее с помощью падающего меню «Система линейных уравнений», нажатием кнопки «Решить», мы находим ответ выведенный на FlexGrid. Там же можем посмотреть блок-схему самого метода Гаусса. В меню «Визуализация» мы можем рассмотреть ответ графически. В меню «Справка» выводится информация об авторе
Формы
Мой проект состоит из исполняемого файла программы kursovaya.exe, исходных файлов программы (папка sources), матрицы с данными об уравнении и пояснительной записки, файла, который вы сейчас читаете.
Интерфейс всей программы

Форма frmSplash
При запуске программы появляется окно заставки frmSplash, при щелчке по форме заставка прячется и загружается главное окно программы:

Окно frmMain
Функции выполняемые пунктами меню
|
Заголовок |
Имя |
Действие |
|
Файл |
mnuFile |
|
|
--Выход |
mnuExit |
Завершение работы приложения |
|
Система линейных уравнений |
mnuEq |
|
|
--Блок-схема алгоритма |
mnuBlockSh |
Открывает форму с блок-схемой алгоритма |
|
--Решение |
mnuDecision |
Открывает форму с решением системы |
|
Окно |
mnuWindow |
Содержит список открытых окон MDIChild |
|
Справка |
mnuHelp |
|
|
--О программа |
mnuAbout |
Открывает форму frmSplash |
Это меню создается с помощью мастера MenuEditor, который вызывается из меню Tools, либо с помощью нажатия на клавиатуре Ctrl+E
Вот он - мастер создания меню.
Форма frmDecision содержит средства для ввода данных и последующего их использования для решения системы с помощью метода Гаусса

Окно frmDecision
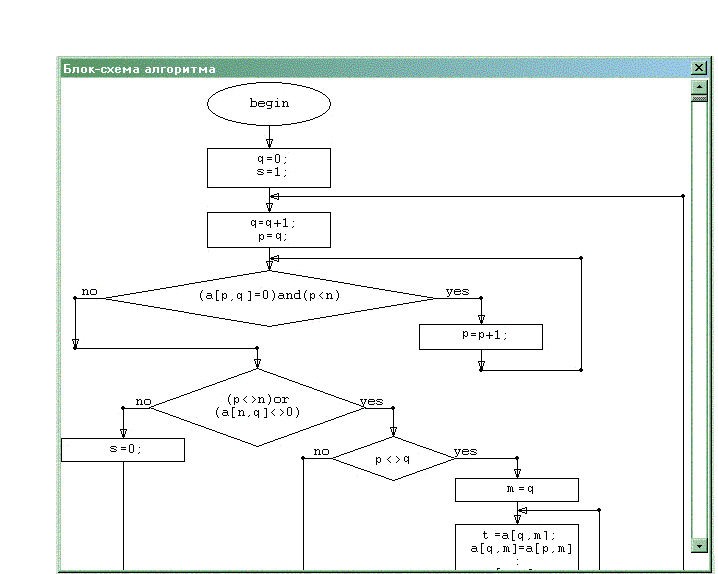
Окно frmBlockSh содержит блок-схему алгоритма решения методом Гаусса
Форма frmVis содержит визуализацию решения при порядке системы равном 2
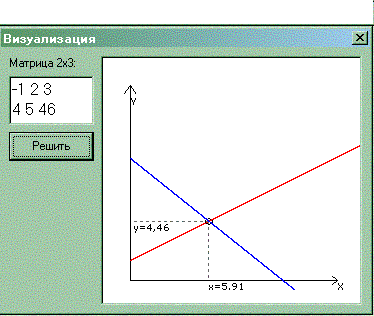
Окно frmVis
