Типовой расчёт
«Кратные интегралы».
Задача 1. Построить область S, заданную следующими неравенствами или уравнениями. Перейти от двойного интеграла
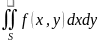
К повторному двумя способами в декартовых координатах и при переходе к полярным координатам.
Задача 2. Построить область S, заданную следующими уравнениями. Вычислить площадь данной области с помощью перехода к новым криволинейным координатам по формуле

Построить область S1.
Задача 3. Вычислить объём тела, образованного пересечением следующих поверхностей, с помощью двойного интеграла.
Задача 4. Вычислить объём тела, образованного пересечением следующих поверхностей, с помощью тройного интеграла.
Задача 5. Вычислить площадь части поверхности Q, вырезаемой поверхностью S.
Задача
6. Вычислить
массу тела, образованного пересечением
следующих поверхностей и имеющего
плотность
 с
помощью тройного интеграла.
с
помощью тройного интеграла.
Задача1.
№вар. |
Условия |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
Задача2.
№вар. |
Условия |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
, |
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
, |
16 |
, |
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
Задача3.
№вар. |
Условия |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9* |
|
10 |
|
11* |
|
12 |
|
13 |
|
14 |
|
15* |
|
16 |
,
, |
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|



 ,
,
 .
.
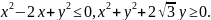
 ,
, .
.
 ,
,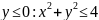 .
.

 .
.
 ,
,
 ,
, .
.

 .
.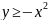 ,
,
 ,
,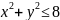
 ,
,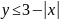
 ,
,
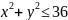
 ,
,

 ,
,

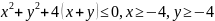
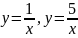 ,
,
 .
. ,
, .
. ,
,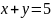 ,
, .
.

 ,
,
 ,
,
 .
.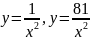 ,
, .
.
 .
. ,
,
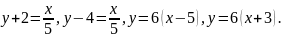
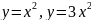 ,
,
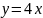


 .
.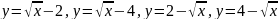 .
.
 ,
,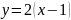 ,
,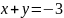 ,
,
 ,
, .
. ,
,
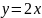 .
.
 ,
, .
.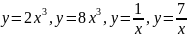 .
. ,
,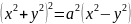 ,
,
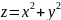 ,
,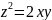 ,
,
 ,
,
 .
. ,
, .
.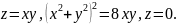
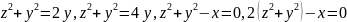
 ,
,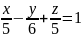 ,
,
 .
. ,
, ,
,
 ,
,

 ,
,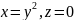

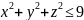 ,
,



 ,
,
 .
. ,
,
,
,
,
,
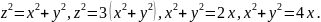
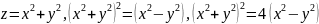 ,
,
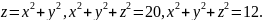
 ,
,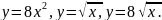

 ,
,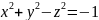 .
.