
2.4. Разложение двухмерного аффинного преобразования
Один из способов разложения может быть таким
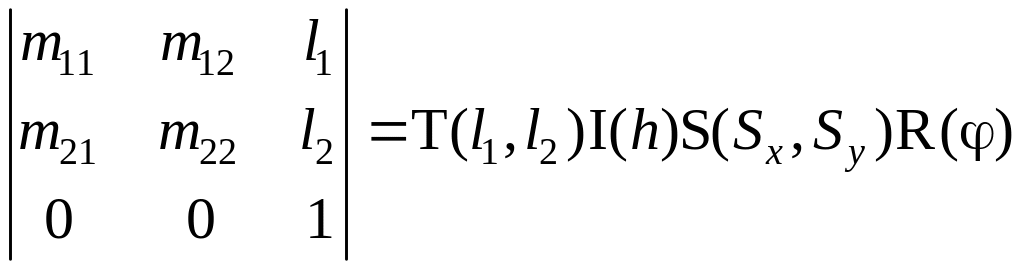 ,
,
где
![]()
![]()
![]()
![]()

Следовательно, любое аффинное преобразование можно понимать как вращение на угол φ, за которым следует масштабирование на Sx и Sy, затем сдвиг на h и завершает перемещение на l1 и l2. Следует заметить, что это разложение не единственно.
Еще одно полезное разложение:
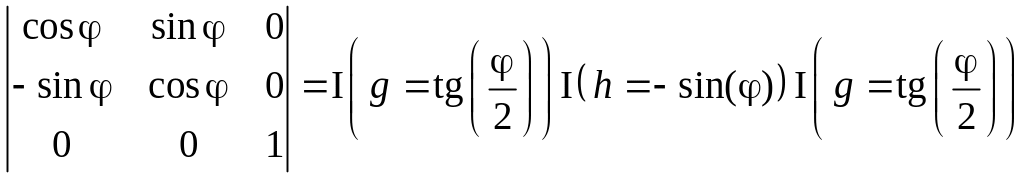 .
.
Такое разложение удобнее использовать при аппроксимации окружности. При этом задача будет решаться быстрее.
2.5. Анимация формы. Твининг
Твининг – широко распространенный метод анимации. Изложение этого приема требует предварительных сведений из теории.
П усть
усть
![]() – система точек;
– система точек;
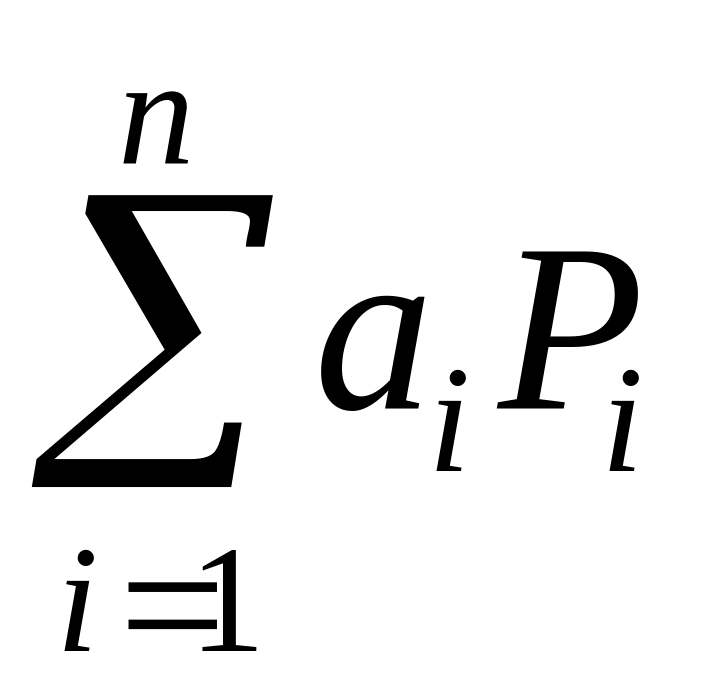 –
линейная комбинация точек,
–
линейная комбинация точек,
![]() ,
если при этом
,
если при этом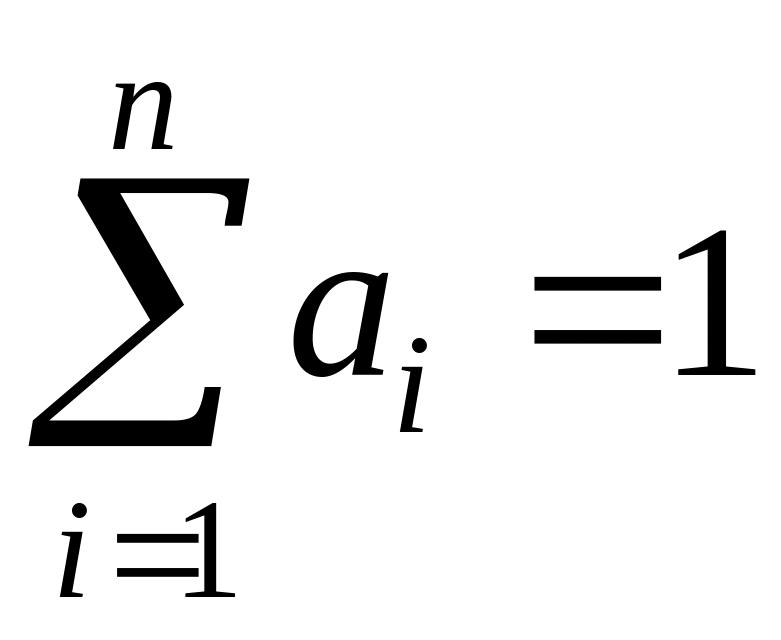 ,
то
образуют аффинную комбинацию точек.
Только аффинная комбинация точек
является точкой. Это означает, что
в общем
случае операция сложения точек не
определена. Суммировать точки и ожидать,
что результат будет точкой, можно, только
если сумма точек образует аффинную
комбинацию.
,
то
образуют аффинную комбинацию точек.
Только аффинная комбинация точек
является точкой. Это означает, что
в общем
случае операция сложения точек не
определена. Суммировать точки и ожидать,
что результат будет точкой, можно, только
если сумма точек образует аффинную
комбинацию.
На
рис. 2.13 точка P
находится как
![]() Здесь a1
= (1–t),
a2
= t;
t
– параметр; t
= 0
1. При этом a1
+
a2
= 1. Следовательно, P
есть аффинная комбинация точек, т.е. P
– точка при любом t,
в заданном интервале.
Здесь a1
= (1–t),
a2
= t;
t
– параметр; t
= 0
1. При этом a1
+
a2
= 1. Следовательно, P
есть аффинная комбинация точек, т.е. P
– точка при любом t,
в заданном интервале.
Результат сложения: при t = 0 P = A при t = 1 P = B. При t = 0,5 P – середина отрезка AB и т.д., т.е. при t = 0→1 точка P будет перемещаться от A до B по прямой, их соединяющей.
Пусть ABC – фигура в начальном положении, A`B`C` – фигура в конечном положении. Тогда промежуточные положения узловых точек при анимации будут:
A`` = (1– t)A + tA`; B`` = (1 – t) B + tB`; C`` = (1 – t)C + tC`.
На
рис. 2.14 показаны промежуточные формы,
которые принимает фигура
![]() при плавном преобразовании в A`B`C`.
Этот прием широко используется в анимации
«преобразование формы», в частности, в
Macromedia
Flash
MX.
при плавном преобразовании в A`B`C`.
Этот прием широко используется в анимации
«преобразование формы», в частности, в
Macromedia
Flash
MX.

2.6. Преобразования модели в 3d
В 3D точка и матрица преобразований в однородной форме имеют вид:
 ;
;
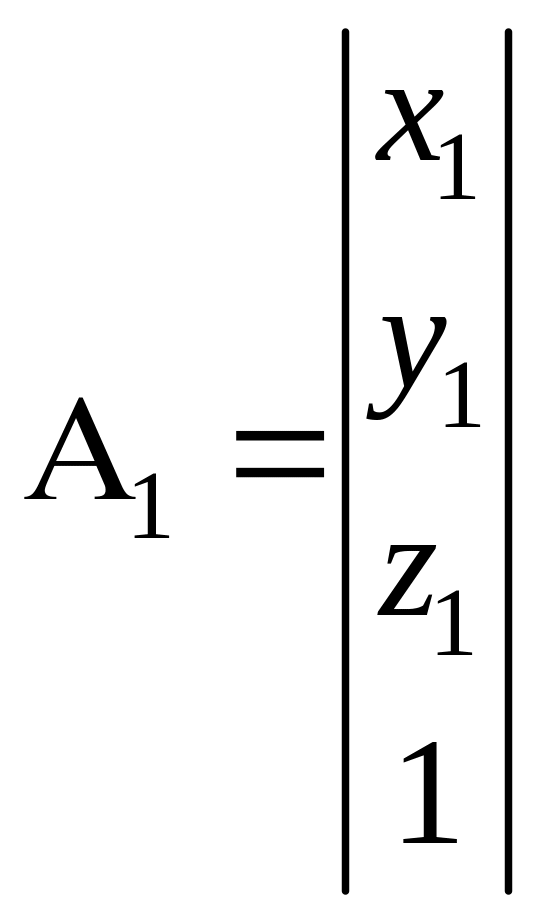 ;
;
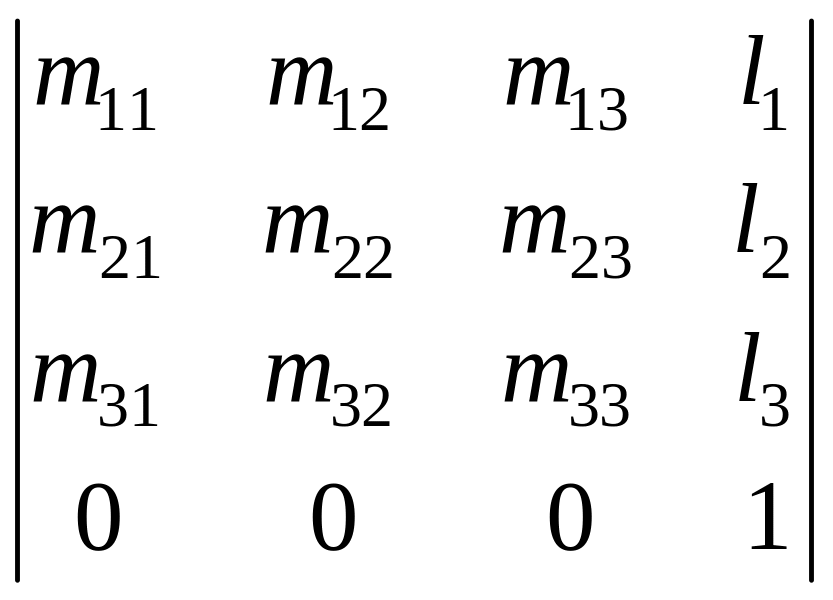 ;
;
![]() .
.
Все формулы для получения результирующего преобразования из последовательности составляющих те же, что и в 2D. Все формулы для получения обратных преобразований те же, что и в 2D.
Элементарные матрицы преобразований в 3D:
1)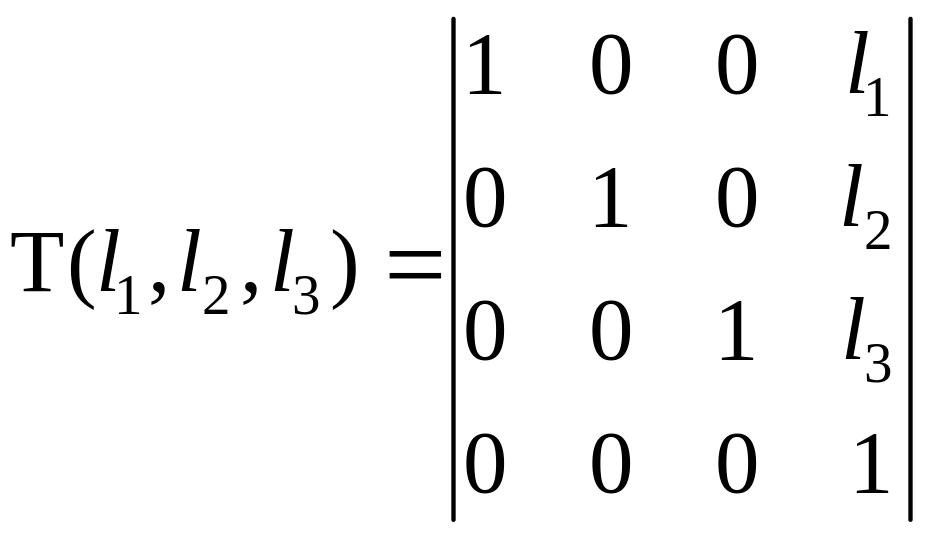 ;
;![]() .
Это – матрица смещения.
.
Это – матрица смещения.
2)
![]() –
матрица вращения вокруг оси, исходящей
из начала координат, направление которой
задается единичным вектором
–
матрица вращения вокруг оси, исходящей
из начала координат, направление которой
задается единичным вектором![]() ,
,
![]() ,
как на рис. 2.15.
,
как на рис. 2.15.
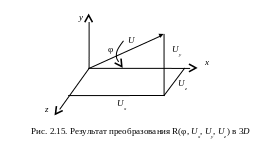
Положительное направление φ – против часовой стрелки, если смотреть из той точки, куда указывает вектор U.
Частные случаи этой матрицы:
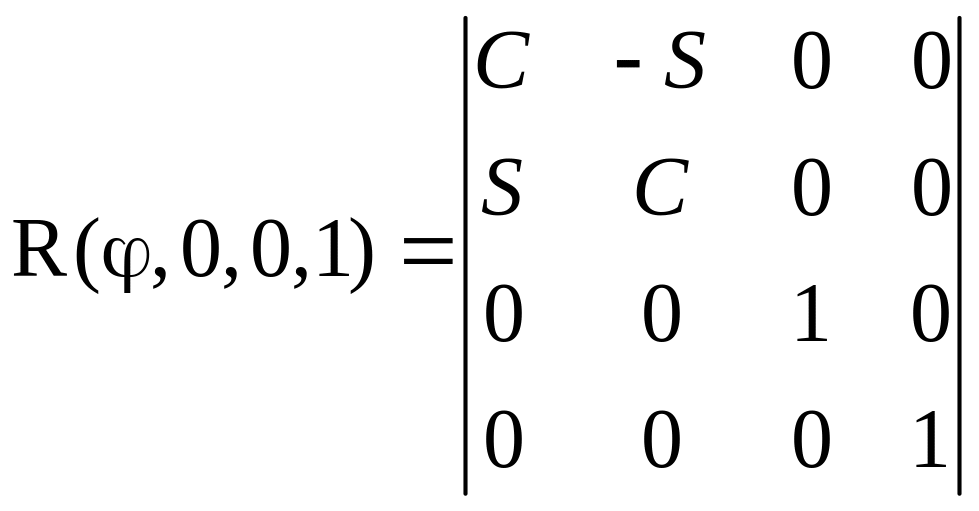 –
вращение
вокруг оси z;
–
вращение
вокруг оси z;
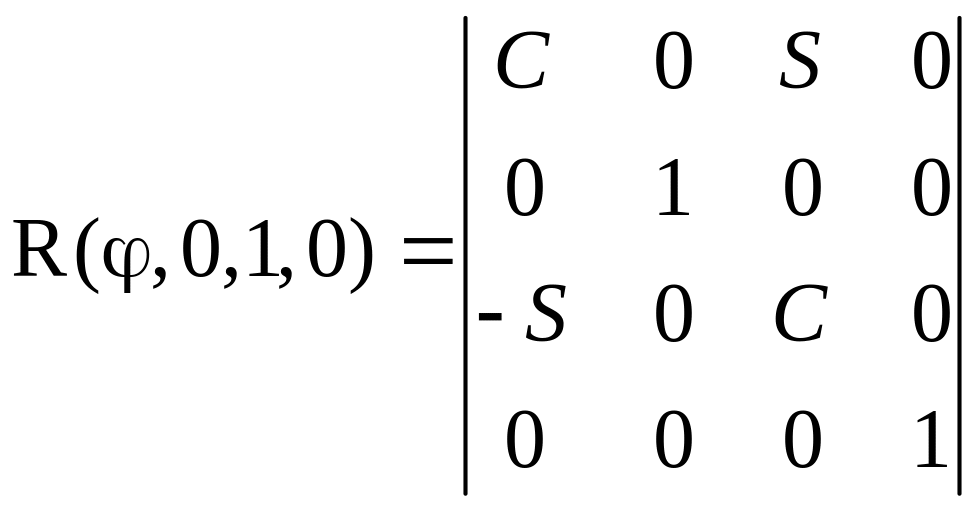 –
вращение
вокруг оси y;
–
вращение
вокруг оси y;
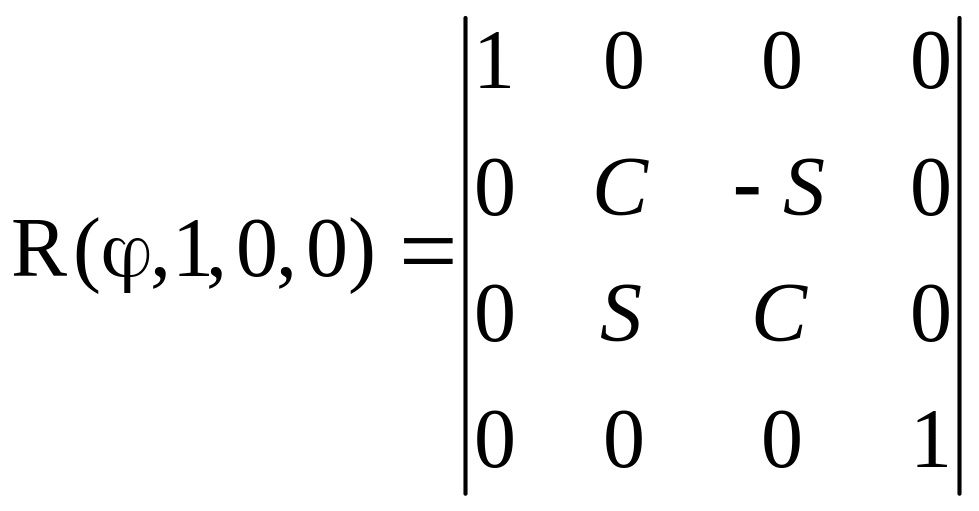 –
вращение
вокруг оси x.
–
вращение
вокруг оси x.
Здесь
приняты такие условные обозначения:![]() ,
,![]() .
.
В общем случае, когда ось вращения не совпадает с координатными осями:
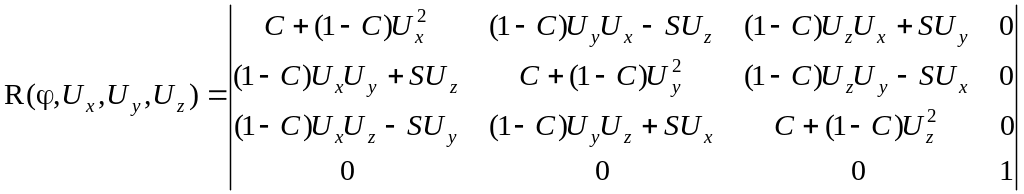
Задача, обратная только что рассмотренной:
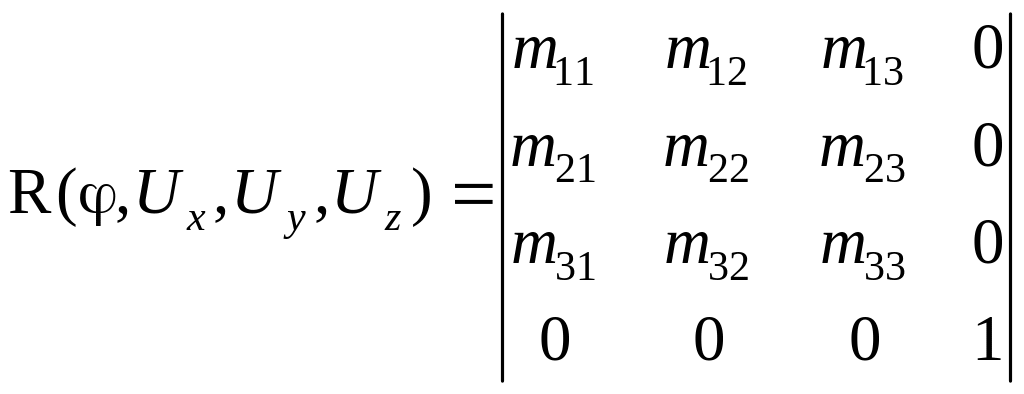 – задано.
Найти φ
и
.
– задано.
Найти φ
и
.
Готовое решение:
![]() ;
;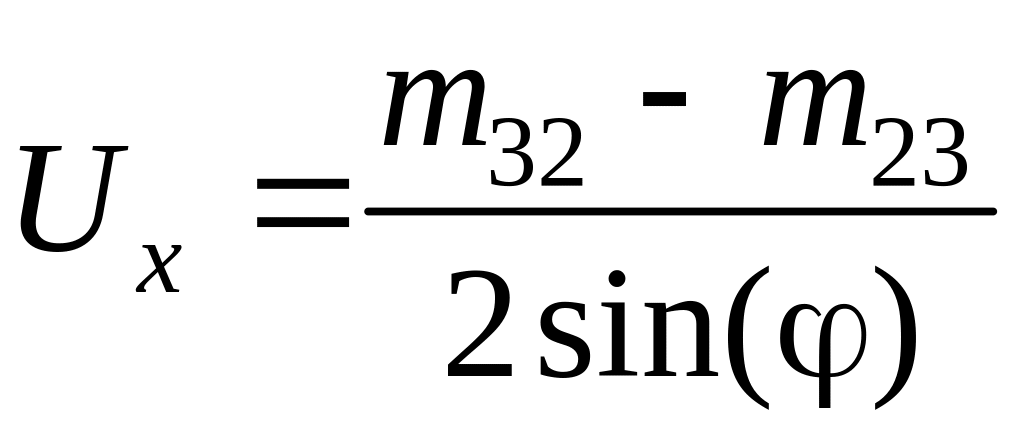 ;
; ;
; .
.
В заключение после ознакомления с аффинными преобразованиями в 3D и с понятием аффинной комбинации точек свойства аффинных преобразований можно дополнить еще такими:
- плоскость преобразуется в плоскость;
- параллельные плоскости преобразуются в параллельные;
- аффинные комбинации точек преобразуются в аффинные.
