2. Преобразование модели

Представляют интерес преобразования двух типов:

- объект задан в некоторой системе координат (СК). Необходимо получить представление этого объекта в той же СК, но после его перемещения, или вращения, или масштабирования, или после любой комбинации таких преобразований. Будем говорить, что это преобразования моделирования или преобразование модели;

- объект задан в некоторой СК0, относительно которой задана новая СК1. Необходимо получить представление этого же объекта в СК1. Будем говорить, что это преобразование координат.

Начнем изучение преобразований с преобразований модели. Преобразования координат имеют много общего с преобразованиями модели, поэтому при изучении этого вопроса будем уже в значительной степени подготовлены.

Кроме того, начнем с 2D и затем расширим полученные результаты на 3D.

И, наконец, будем исходить из следующего – в компьютерной графике объект любой сложности представляет собой совокупность точек (вершин). Отрезок – две точки, контур – совокупность отрезков, грань – замкнутый контур, объект 3D – совокупность граней.

Поэтому все задачи преобразования будем изучать как преобразования над точкой, понимая, что если применить эти преобразования над всеми вершинами объекта, то и получим нужным образом преобразованный объект.

2.1. Преобразование модели в 2d

Пусть в СК XY задана точка A₀(x₀, y₀), как на рис. 2.1.

Выполним такие преобразования:

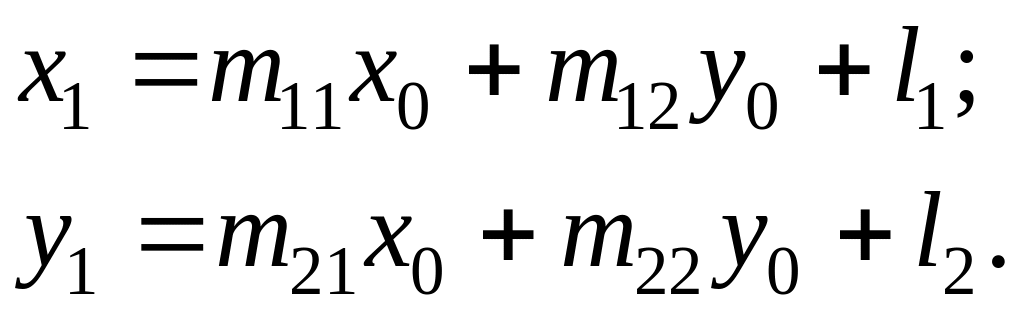(2.1)

Ясно, что в общем случае и , следовательно, можно говорить о какой-то другой точке A₁(x₁, y₁). Но можно говорить, что это та же точка A, которая в результате преобразований (2.1) переведена из положения A₀(x₀, y₀) в положение A₁(x₁, y₁). Условные обозначения: A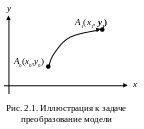 – точка; A₀(x₀, y₀) или А₀ – точка A в начальном положении 0; A₁(x₁, y₁) или А₁ – точка A в положении 1, в которое она переводится преобразованием (2.1).

Если m₁₁, m₁₂, m₂₁, m₂₂, l₁ и l₂ – действительные (целые или вещественные), то такие преобразования называют аффинными.

Удобно использовать более компактную матричную форму записи преобразований (2.1):

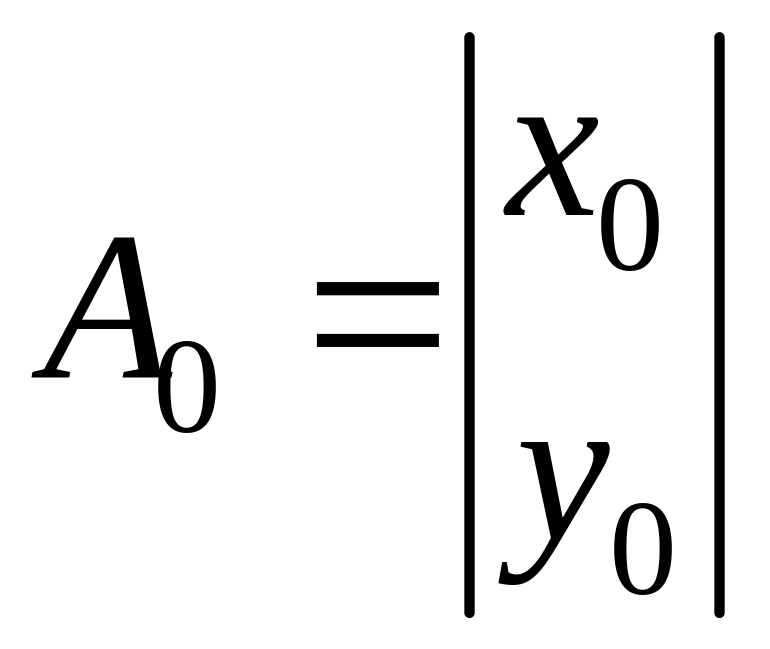– столбец;

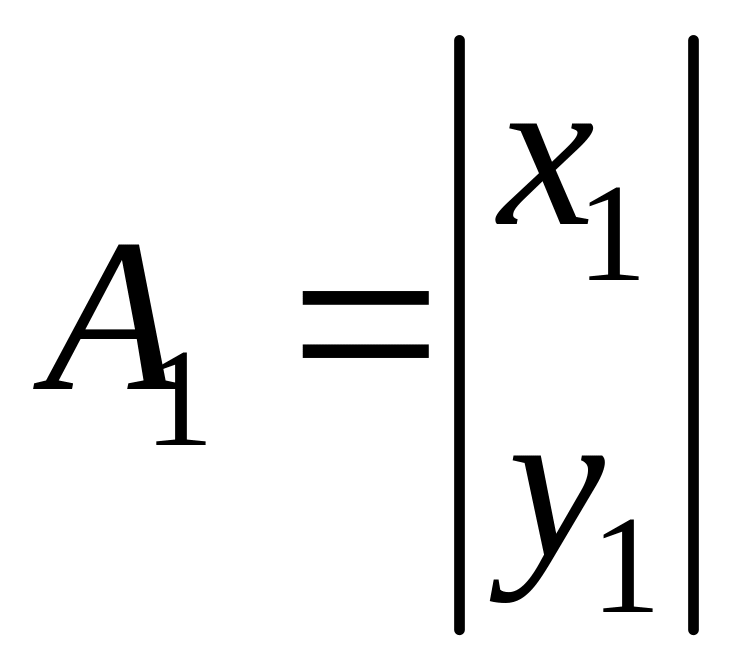– столбец;

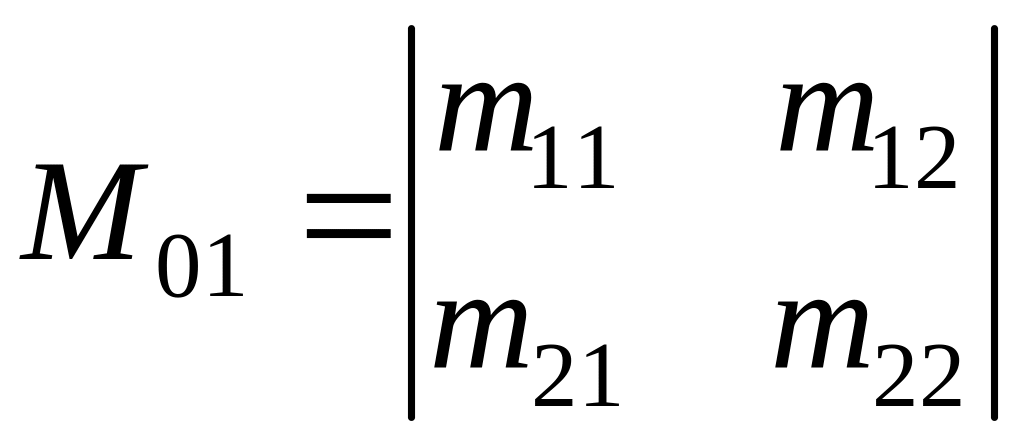– матрица 22;

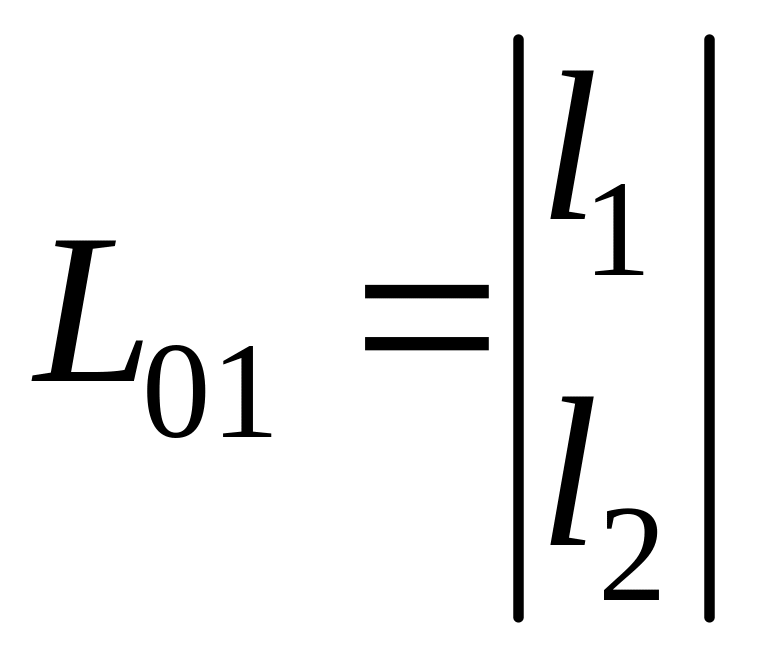– столбец.

Тогда запись преобразования 2.1 примет вид:

. (2.2)

Графически изображать преобразование (2.2) будем так:

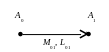
Индексы у М₀₁ и L₀₁ показывают, что эти матрицы участвуют в переводе точки A из положения A₀ в положение A₁. Можно представить сложное перемещение точки А, состоящее из последовательности простых, например, как это показано на рис. 2.2.

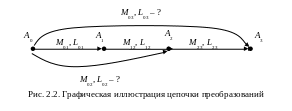
Найдем параметры преобразований M₀₂, L₀₂ и M₀₃, L₀₃:

1) ;

2) ;

; ; ; (2.3)

3)

= ;

; ; . (2.4)

Такой способ вычислений алгоритмически не очень удобен, поскольку при увеличении длины цепочки преобразований расчетные формулы каждый раз меняются, все более усложняясь.

В компьютерной графике принято использовать представление точки в однородной форме. В 2D это делается так:

– точка в физических координатах,

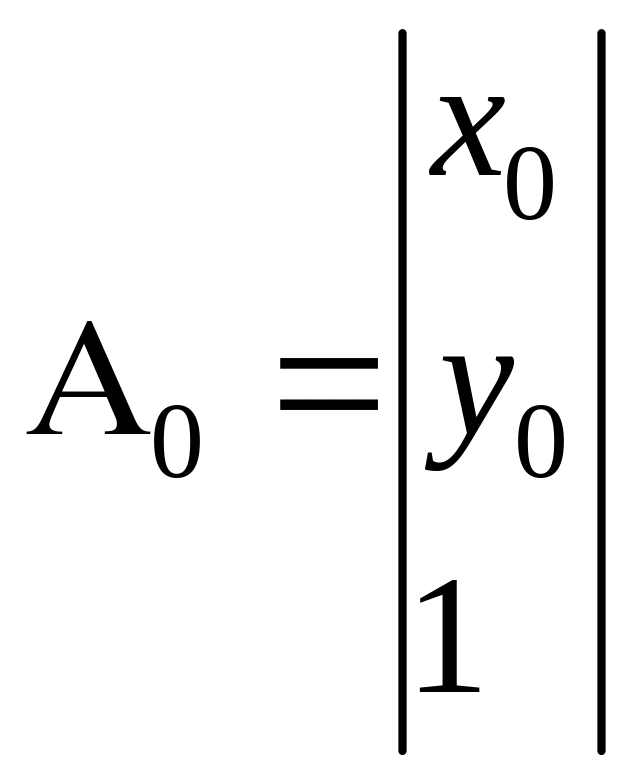– та же точка в однородной форме;

A₀ и А₀ – одна и та же точка, только в разных формах представления.

Введем понятие матрицы преобразования в однородной форме:

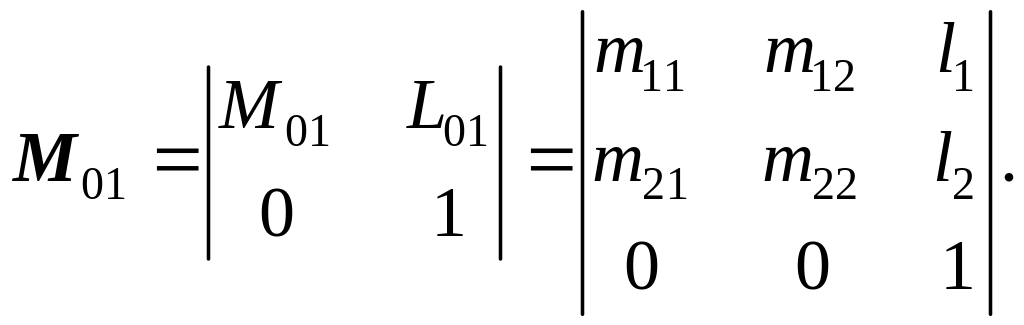
Это матрица преобразования в однородной форме для 2D. Далее будем применять стиль курсив для точек и матриц, когда подразумевается их представление в физических координатах, и нормальный стиль (прямое написание), когда подразумевается их представление в однородной форме.

Найдем результат такого произведения

.

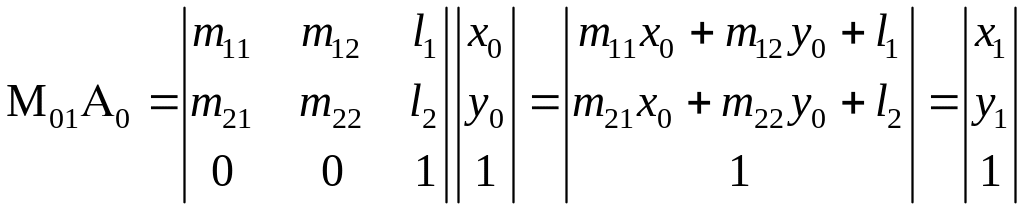Полученный результат сравним с формулой (1) и убеждаемся, что это есть представление в однородной форме точки A₁. Следовательно

(2.5)

Сравним формулы (2.2) и (2.5). Это одно и тоже преобразование, но формула (2.2) – это преобразования в привычных нам физических координатах, а (2.5) – в однородной форме. Форма (2.5) предпочтительнее, ибо она более компактна.

Э тот эффект усиливается при выполнении цепочки преобразований. Вернемся к рис. 2.2 и построим аналогичный ему рис. 2.3, но в терминах однородных координат.

На рис. 2.3 M₀₁, M₁₂ и M₂₃ – матрицы преобразования в однородной форме, переводящие точку из положения A₀ в положения A₁, A₂ и A₃ соответственно.

Решим ту же задачу. Найдем преобразования, переводящие точку в A₂ и A₃ из A₀.

– этот результат уже получен и он аналогичен формуле (2.2).

– этот результат аналогичен формуле (2.3), но он выгодно отличается компактностью.

– этот результат аналогичен формуле (2.4), здесь эффект еще более силен.

Справедливы такие формулы:

,

,

,

.

В общем случае для цепочки преобразований:

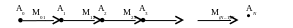
, ; (2.6)

. (2.7)

Выводы из предыдущего материала: преобразования в однородной форме обладают высокой алгоритмической привлекательностью. Матрица сложного преобразования, являющегося последовательностью составляющих его, получается простым произведением матриц, задающих составляющие преобразования (см. формулы (2.6) и (2.7)).

До сих пор не известно, какие значения следует назначать элементам матрицы M₀₁ с тем, чтобы точка перемещалась строго определенным образом. Научимся назначать значения элементам матрицы M₀₁ целенаправленно.

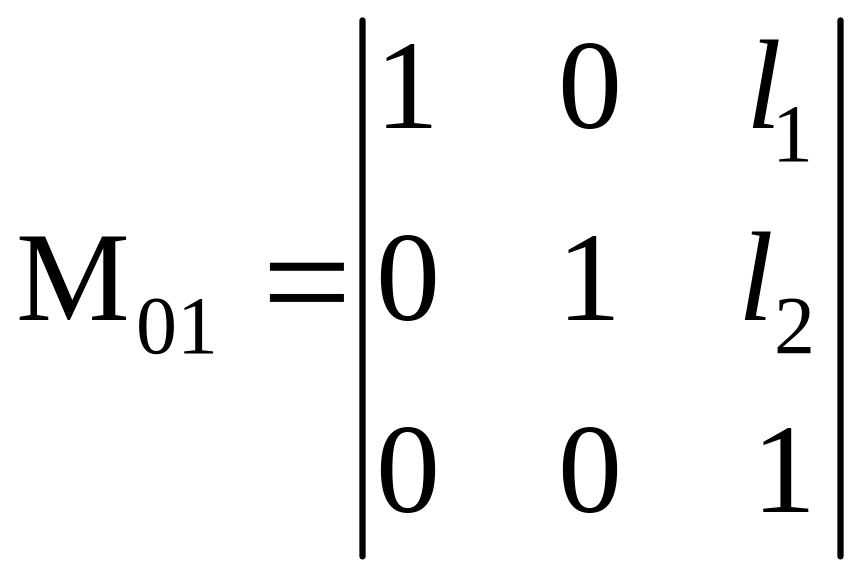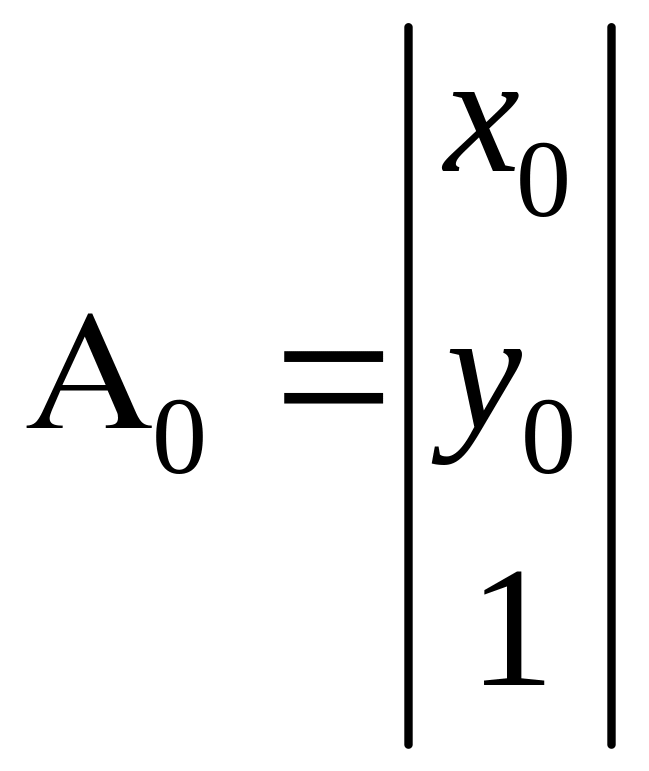1. Пусть и , тогда

.

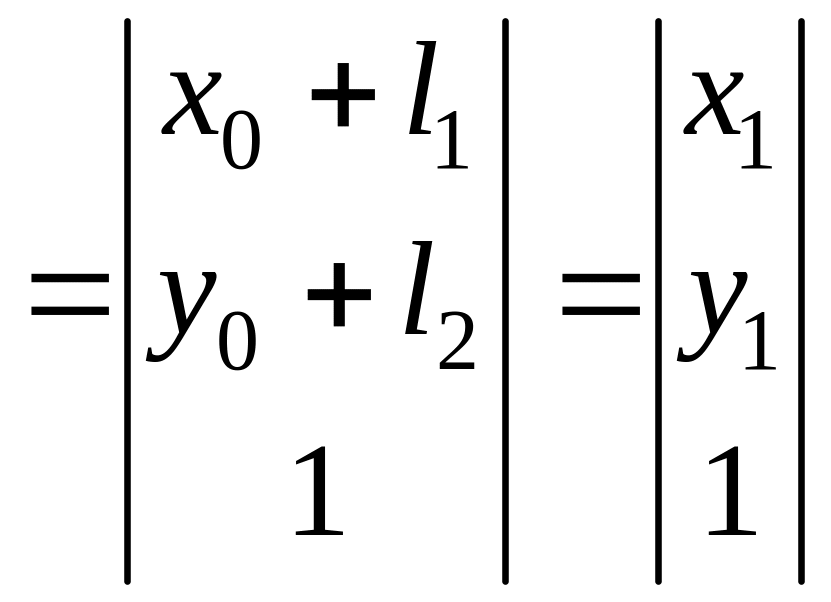Т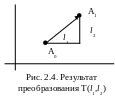 аким образом, рассматриваемая матрица M₀₁ будучи применена к точке A₀ переводит ее в положение A₁ как на рис. 2.4.

Рассматриваемую матрицу целесообразно выделить как типовую элементарную матрицу, задающую преобразование смещения и обозначать ее будем T или T(l₁, l₂) в зависимости от того, как это требуется из контекста, т.е.

.

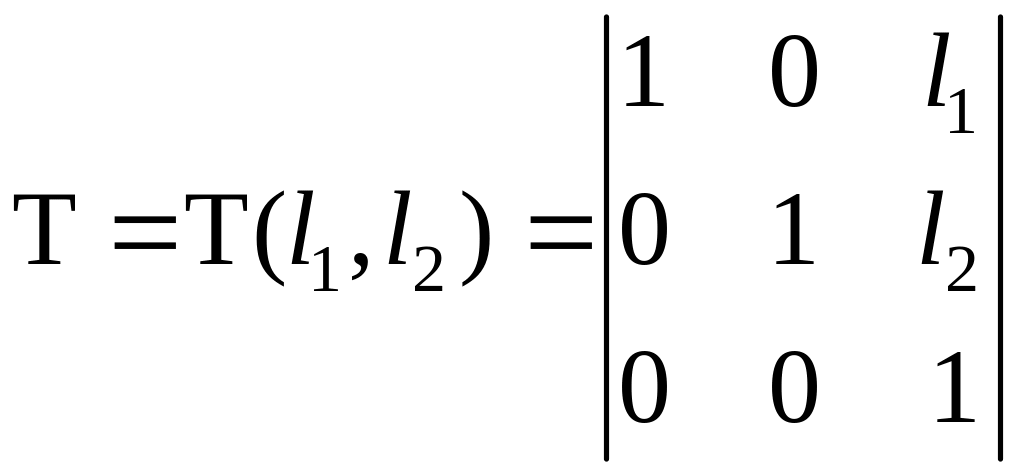2. Пусть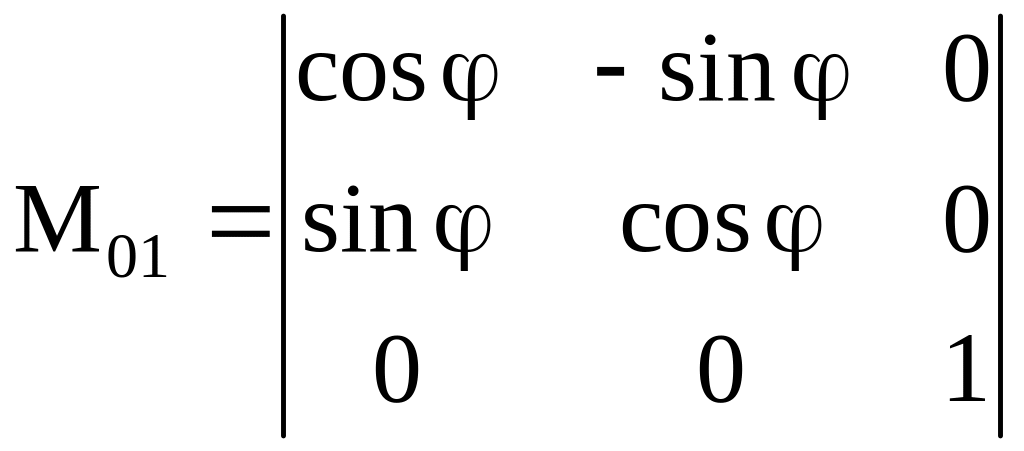 ; , тогда .

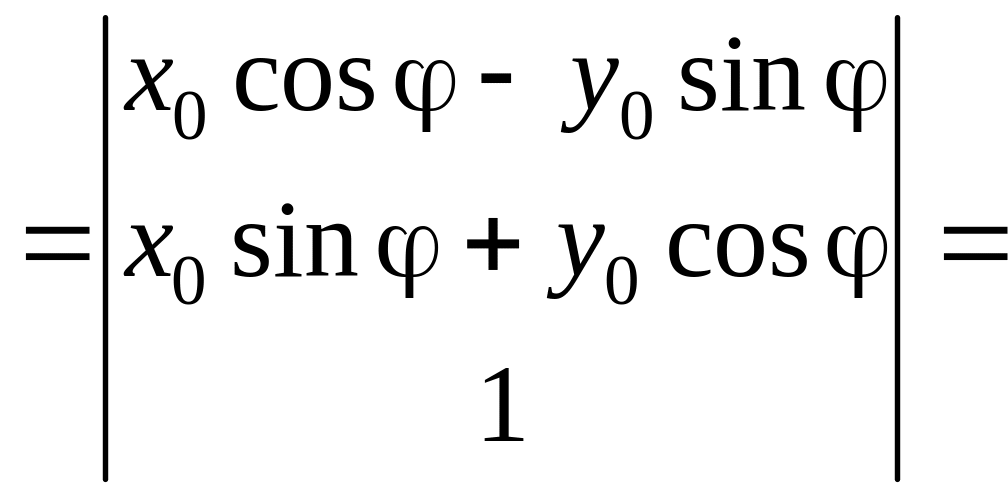
О братимся к рис. 2.5.

Если точку A₀ повернуть в положительном направлении (против часовой стрелки) на угол φ, то она примет положение A₁. Если элементарными средствами тригонометрии вычислить координаты x₁ и y₁ точки A₁ на этом рисунке, то получим тот же результат для x₁ и y₁, который получен ранее при выполнении операции .

Таким образом, рассматриваемая матрица M₀₁ будучи примененной к точке A₀ поворачивает ее на угол φ в положительном направлении как на рис. 2.5. Эту матрицу целесообразно выделить как очередную типовую элементарную матрицу, задающую преобразование вращения, и обозначать ее будем R или R(φ), т.е.

.

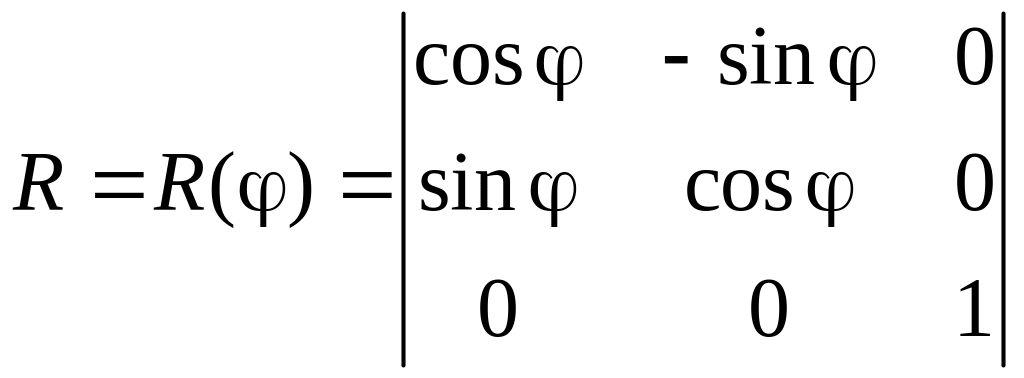3. Пусть 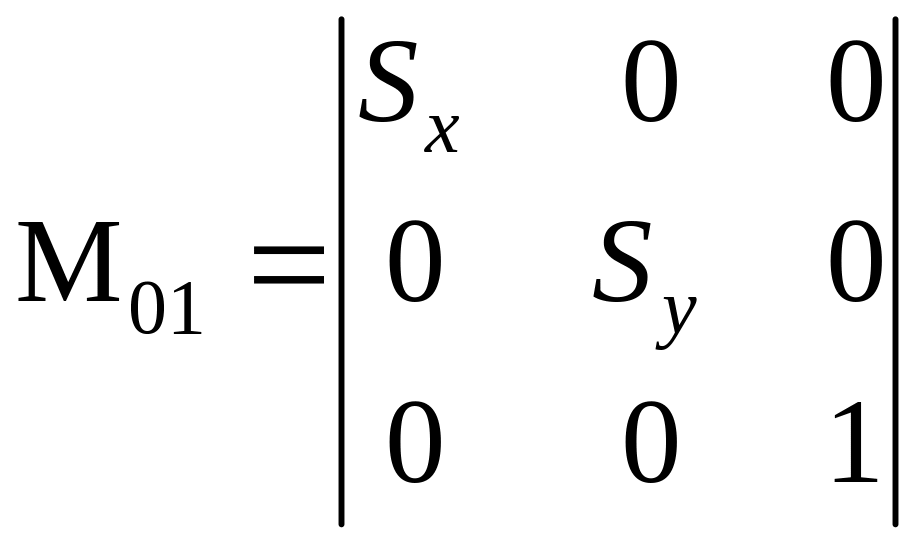и , тогда

= .

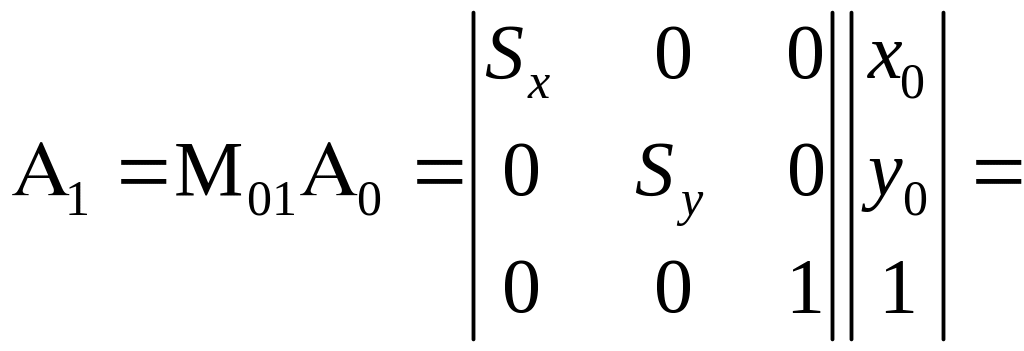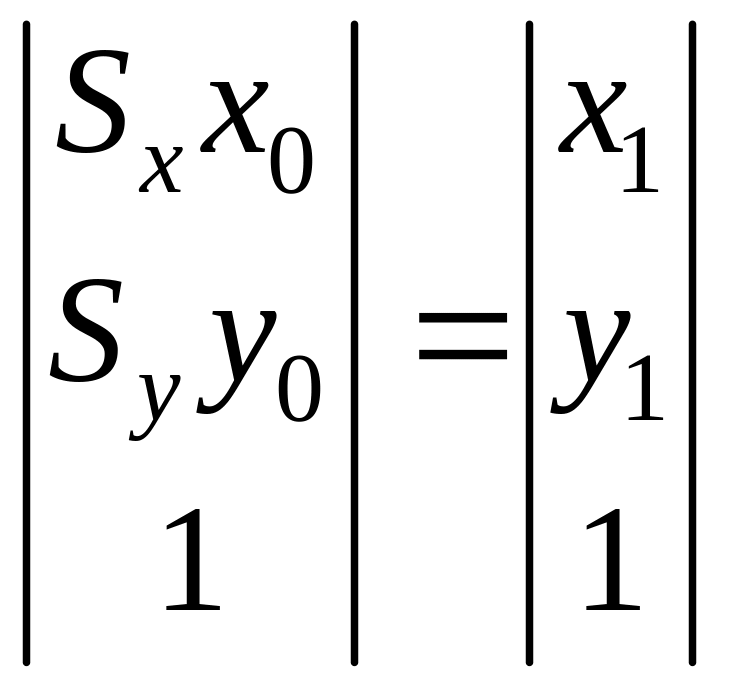Здесь x – координата точки A₀ масштабируется на коэффициент S_x; y – на коэффициент S_y. Рассматриваемую матрицу можно выделить как следующую типовую элементарную матрицу, задающую преобразование масштабирования, и обозначать ее будем S или S(S_x, S_y), т.е.

.

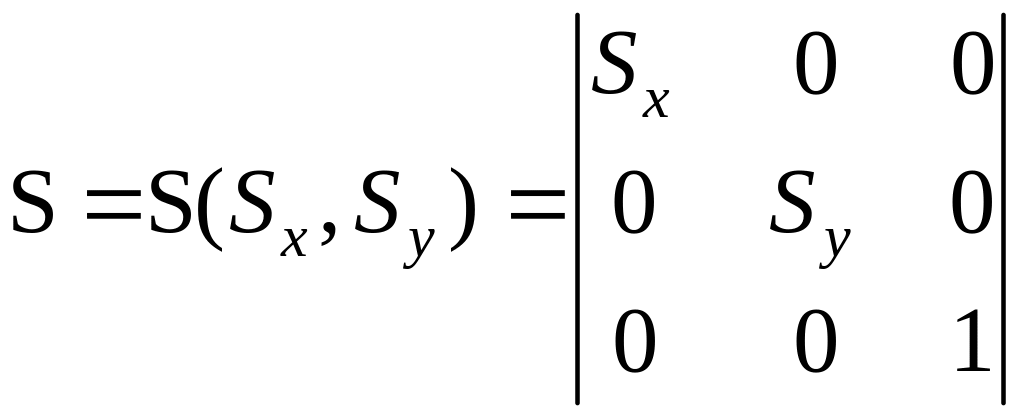Матрица масштабирования имеет несколько полезных частных случаев.

; .

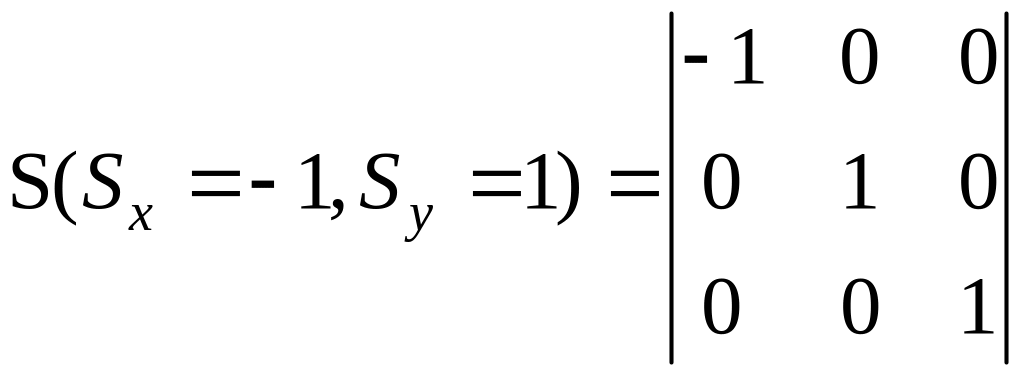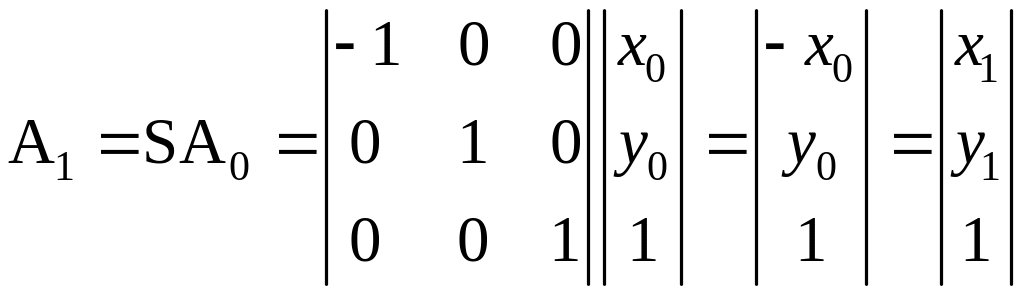И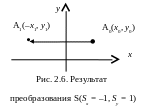 з рис. 2.6 видно, что преобразование S(S_x = –1, S_y = 1) есть зеркальное отражение относительно оси y. Аналогично матрица осуществляет зеркальное отражение относительно оси x, матрица – относительно осей x и y одновременно.

4. Пусть 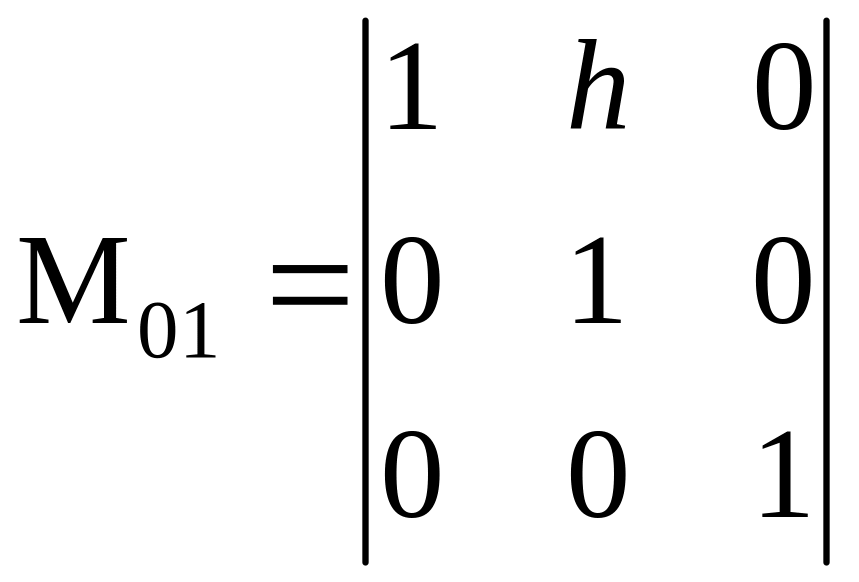и , тогда .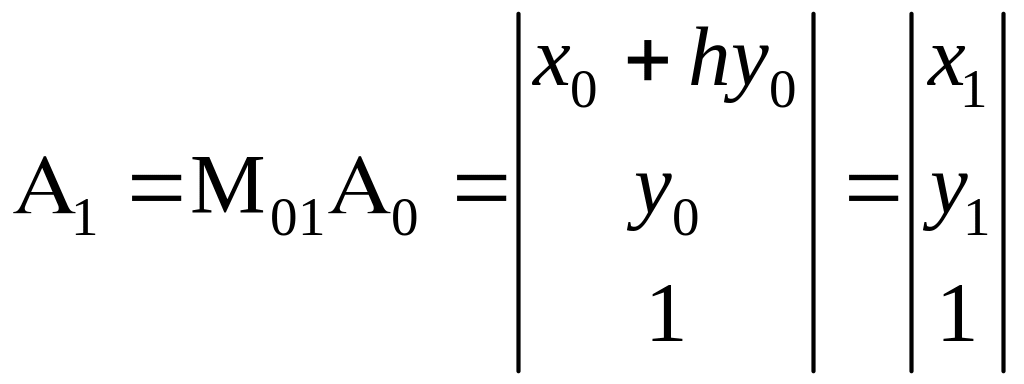

Здесь точка смещается вдоль оси x на величину, пропорциональную y₀ и h. Рассматриваемую матрицу можно выделить как типовую элементарную, задающую преобразование сдвига в x направлении, как на рис. 2.7.

Аналогично можно создать матрицу сдвига в y направлении 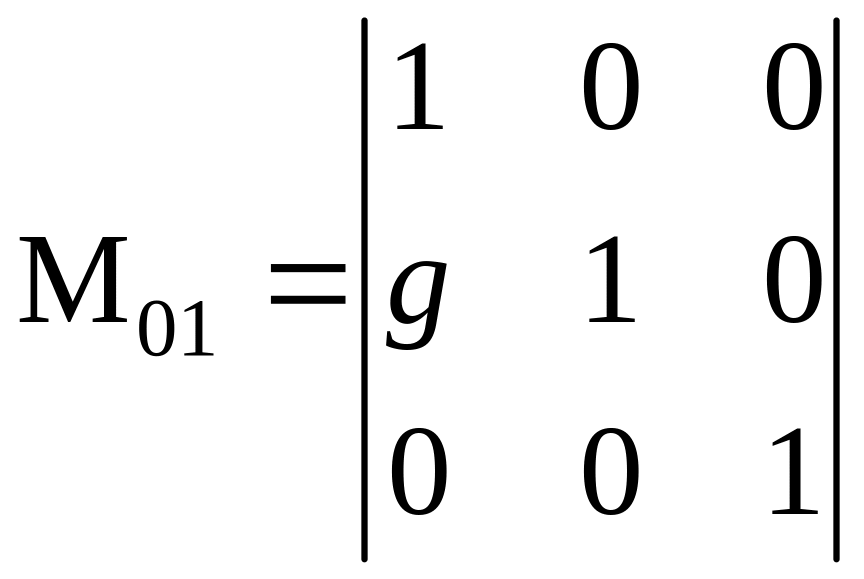и тогда 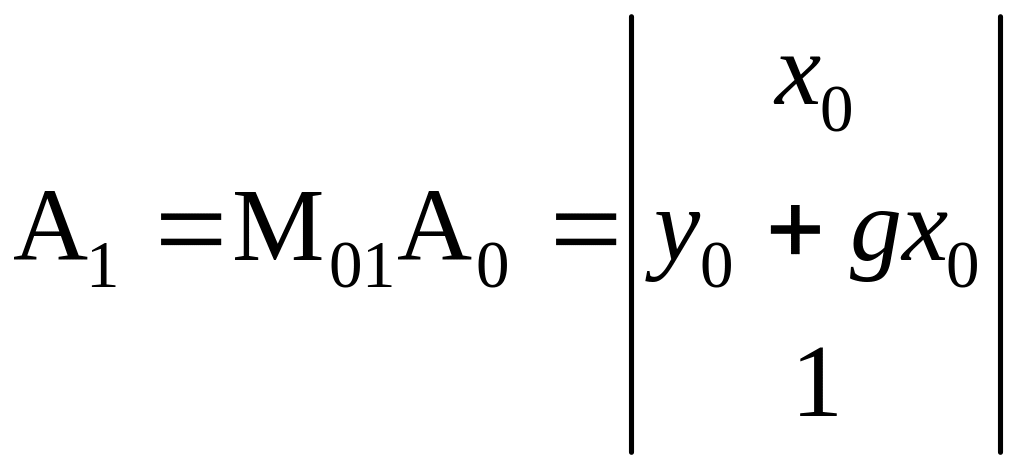. На рис. 20 показано это преоб­разование.

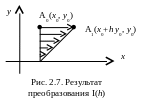
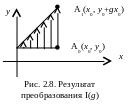
Рассматриваемую матрицу можно выделить как типовую элементарную, осуществляющую преобразования сдвига, обозначать ее будем I или I(h), или I(g):

, .

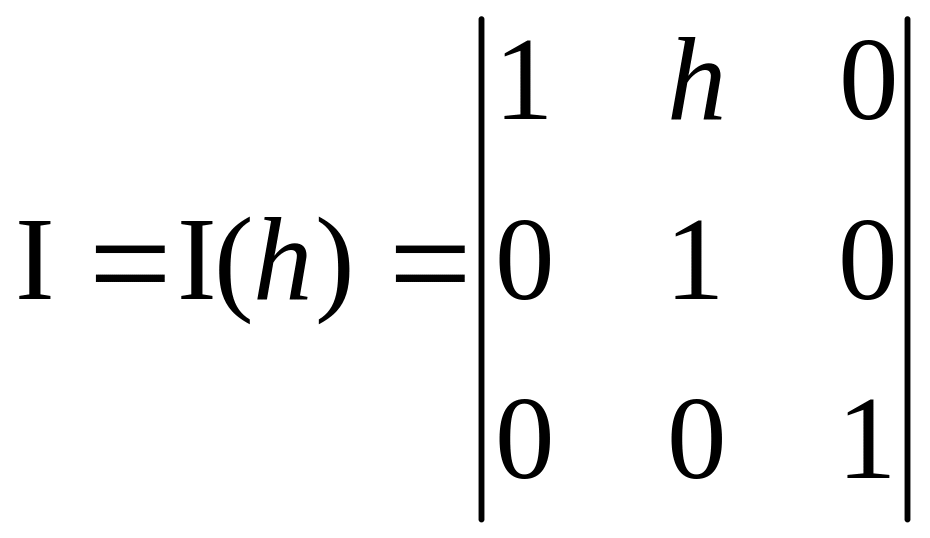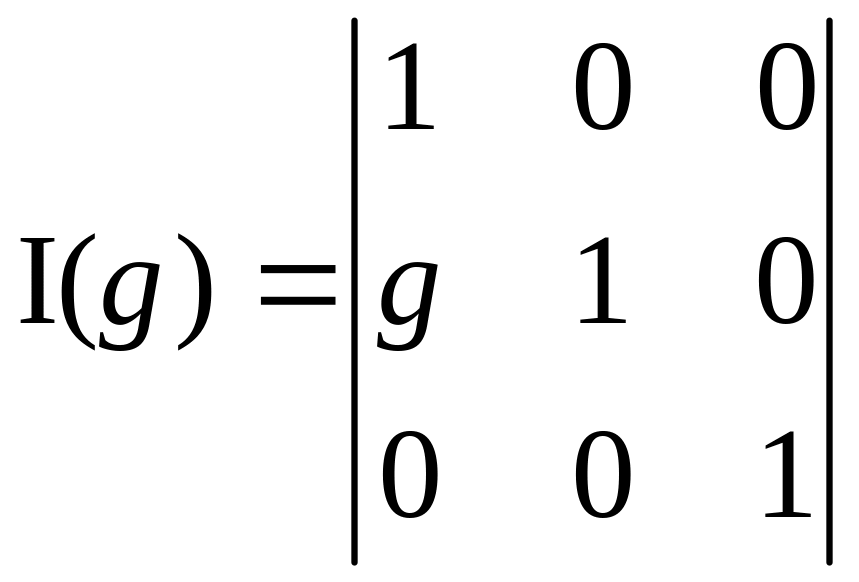Матрицы T, R, S и I задают элементарные преобразования, из которых может быть построено любое, как угодно сложное.

Пример. Построить матрицу вращения точки A₀ на угол φ вокруг точ­ки A(a_x, a_y).

1) Матрицу R(φ) напрямую для этих целей использовать нельзя, ибо она осуществляет поворот вокруг начала координат.

2) Переместим точку A₀ на (–a_x, –a_y) в положение A₁, при этом положение A₁ относительно начала координат, будет такое же, как положение A₀ относительно A. Матрица такого преобразования будет M₀₁=T(–a_x, –a_y).

3) Повернем точку A₁ на угол φ относительно начала координат. Точка примет положение A₂. Матрица такого преобразования будет .

4) Переместим точку A₂ на (a_x, a_y) в положение A₃, при этом точка A₃ окажется в положении, как если бы точку A₀ повернули на угол φ вокруг точки A. Соответствующая матрица будет M₂₃= T(a_x, a_y).

Результирующее преобразование в соответствии с правилом (2.7) будет:

;

.

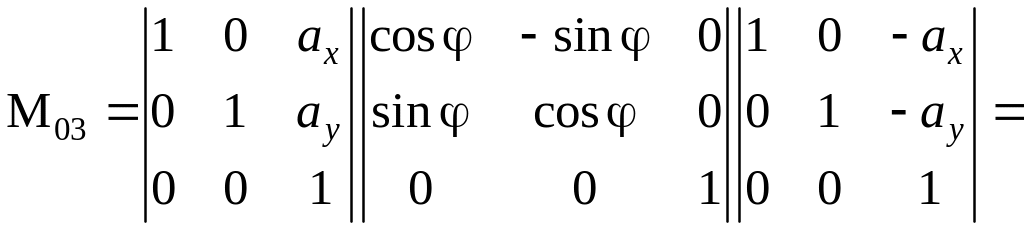
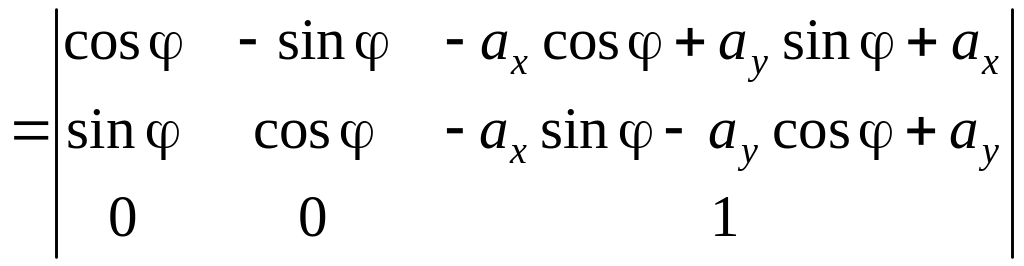Это прекрасная иллюстрация того, как сложное движение конструируют как последовательность элементарных движений, для каждого из которых составляют матрицу преобразования и результирующее преобразование получают как их произведение по правилу (2.7).