Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет физико-математических и компьютерных наук

Кафедра прикладной математики и информационных технологий

Специальность 010500 – «Информационные системы и технологии»

Курсовая работа

по дисциплине “Языки и методы программирования”

на тему:

Рекуррентные формулы. Рекурсивные алгоритмы и подпрограммы

Выполнила:

студентка 1 курса

группы ИС-1

Герасимчук Анастасия

________________________

(подпись студента)

_____________________________________

(оценка)

Научный руководитель:

к.т.н., доцент

Воробьёв Григорий Алексеевич

________________________

(подпись преподавателя)

Липецк 2012

Оглавление

ВВЕДЕНИЕ 3

Глава 1. Теоретические основы применения рекурсии в программировании 5

Глава 2. Рекурсия в среде программирования delphi 20 введение

Полезность, важность и необходимость рекурсии, как одного из концептуальных методов решения практических задач известна всем программистам.

Американский специалиста по системному программированию Д.Кнут, например, широко использовал рекурсию при изложении материала в ставшем уже классическим трехтомнике “Искусство программирования для ЭВМ”. Английскому теоретику информатики Ч.Хоару принадлежат следующие слова “Следует отдать должное гению разработчиков Алгола-60 за то, что они включили в свой язык рекурсию и дали мне тем самым возможность весьма элегантно описать мое изобретение (речь идет о так называемой быстрой сортировке Хоара – Quick Sort). Сделать возможным изящное выражение хороших мыслей – я считал это наивысшей целью проекта языка программирования”. На сегодняшний день, практически все действующие языки программирования поддерживают рекурсию.

Цель курсовой работы знакомство с применением рекурсии в программировании.

Задачи работы:

1. проанализировать научно-методическую литературу по теме исследования;

2. познакомиться с понятиями рекуррентных формул в математике, рекурсивных алгоритмов и подпрограмм;

3. проанализировать некоторые распространенные рекурсивные алгоритмы;

4. освоить возможности среды Delphi по организации рекурсивных процедур и функций;

5. разработать примеры рекурсивных алгоритмов, процедур и функций.

В курсовой работе дается неформальное понятие рекурсии, рассказывается об общей схеме решения задач с помощью рекурсии и приведены рекурсивные алгоритмы решения весьма разнообразных по содержанию и степени сложности задач.

Глава 1. Теоретические основы применения рекурсии в программировании

1. Рекуррентные формулы в математике

Рекуррентным соотношение, рекуррентным уравнением или рекуррентной формулой называется соотношение вида , которое позволяет вычислять все члены последовательности , если заданы ее первые членов.

Примеры.

1. Формула задает арифметическую прогрессию.

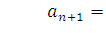2. Формула определяет геометрическую прогрессию.

3. Формула 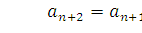задает последовательность чисел Фибоначчи.

В случае, когда рекуррентное соотношение линейно и однородно, т.е. выполняется соотношение вида:

(1)

( ), последовательность называется возвратной.

Многочлен

(2)

называется характеристическим для возвратной последовательности { .

Корни многочлена называются характеристическими.

Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим решением.

Описание общего решения (1) имеет аналоги с описание решения обыкновенного дифференциального уравнения с постоянными коэффициентами.

Теорема 1. 1.Пусть λ – корень характеристического многочлена (2). Тогда последовательность {с }, где с – произвольная константа, удовлетворяет соотношению (1).

2. Если , - простые корни характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид , где , , … , - произвольные константы.

3. Если - корень кратности ( ) характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид

,

где - произвольные константы.

Зная общее решение рекуррентного уравнения (1), по начальным условиям можно найти неопределенные постоянные и тем самым получить решение уравнения (1) с данными начальными условиями.

Пример 1.Найти последовательность { }, удовлетворяющую рекуррентному соотношению и начальным условиям

Корнями характеристического многочлена являются числа . Следовательно, по теореме 1 общее решение имеет вид . Используя начальные условия, получаем систему

Решая которую, находим Таким образом, .

Рассмотрим неоднородное линейное рекуррентное уравнение

(3)

Пусть { } – общее решение однородного уравнения (1), а { } – частное (конкретное) решение неоднородного уравнения (3). Тогда последовательность { } j, образует общее решение уравнения (3), и тем самым справедлива

Теорема 2. Общее решение неоднородного линейного рекуррентного уравнения представляется в виде суммы общего решения соответствующего однородного линейного рекуррентного уравнения и некоторого частного решения неоднородного уравнения.

Таким образом, в силу теоремы 1 задача нахождения общего решения рекуррентного уравнения (3) сводится к нахождению некоторого частного решения.

В отдельных случаях имеются общие рецепты нахождения частного решения.

Если ( где β не является характеристическим корнем), то, подставляя в (3), получаем и отсюда , т.е. частное решение можно задать формулой .

Пусть - многочлен степени от переменной и число 1 не является характеристическим корнем. Тогда и частное решение следует искать в виде . Подставляя многочлены в формулу (3) получаем

Сравнивая коэффициенты в левой и правой частях последнего равенства, получаем соотношения для чисел , позволяющие эти части определить.

Пример 2. Найти решение уравнения

С начальным условием .

Рассмотрим характеристический многочлен Так как и правая часть уравнения (3) равна , то частное решение будем искать в виде . Подставляя в уравнение (4), получаем . Приравнивая коэффициенты в левой и правой частях последнего равенства, получаем систему

Откуда находим Таким образом, частное решение уравнения (4) имеет вид . По теореме 1 общее решение однородного уравнения задается формулой , и по теореме 2 получаем общее решение уравнения (4): . Из начального условия находим , т.е. . Таким образом, .