1.4Свойства определителей.

1). Если в определителе строки заменить столбцами (столбцы строками), то определитель не изменится: .

2). Определитель, содержащий строку (столбец) нулевых элементов, равен нулю.

3). Если в определителе поменять местами две строки (столбца), определитель изменит знак на противоположный.

4). Определитель, содержащий две одинаковые строки (столбца), равен нулю.

5). Если все элементы строки (столбца) определителя умножить на некоторое число, то определитель умножится на это число.

6).Определитель, содержащий две пропорциональных строки (столбца), равен нулю.

7).Если каждый элемент i - й строки определителя  равен сумме двух слагаемых: , то  можно представить в виде суммы двух определителей: , где в определителе  i - я строка состоит из элементов , в определителе  - из элементов , а остальные строки этих определителей совпадают с соответствующими строками определителя .

Аналогичное свойство справедливо для столбцов определителя.

8). Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число.

9). Определитель произведения матриц равен произведению определителей этих матриц .

Иными словами: перемножать определители, записанные в виде таблицы чисел, можно по правилу умножения матриц.

1.5Свойства определителей.

При вычислении определителя можно использовать соответствующее определение определителя или теорему о разложении определителя по элементам строки (столбца). Вычисление определителей второго и третьего порядков при этом обычно не вызывает затруднений. Сложнее обстоит дело с вычислением определителей высших порядков. Так, вычисляя определитель четвертого порядка путем разложения его по элементам строки или столбца, придется вычислять 4 определителя третьего порядка - соответствующие алгебраические дополнения. Для определителя пятого порядка необходимо вычислить 5 определителей четвертого порядка, с учетом предыдущего рассуждения - 20 определителей третьего порядка !

Задача упрощается, если в строке (столбце), по которой разлагается определитель, есть элементы, равные нулю. Тогда алгебраические дополнения этих элементов вычислять не нужно, т.к. соответствующие слагаемые в разложении определителя равны нулю из-за умножения на нулевые элементы.

Используя свойства определителей (свойство 8), можно, не меняя значения определителя, в любой его строке или столбце сделать все элементы, за исключением одного , равными нулю, а затем разложить определитель по элементам этой строки или столбца.

Пример 8. Вычислить определитель

.

В первой строке определителя уже есть два нулевых элемента. Преобразуем определитель так, чтобы еще два элемента этой строки обратились в 0 . Сделать это можно путем преобразований столбцов. Оставим без изменения 2-й и 5-й столбцы (там уже стоят нули). К 3-му столбцу прибавим 1-й, умноженный на -2, к 4-му - первый, умноженный на 1. При этом первый столбец в преобразованном определителе останется без изменения.

Теперь разложим определитель по элементам первой строки:

В полученном определителе четвертого порядка преобразуем к нулю первые три элемента 1-й строки с помощью последнего 4-го столбца: к 1-му прибавим 4-й, умноженный на 3, 2-й преобразовывать не нужно, к 3-му прибавим 4-й, умноженный на -1.

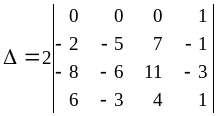
Разложим этот определитель по элементам первой строки:

Полученный определитель третьего порядка можно вычислить по правилу треугольников, однако проще и здесь получив нули (легче всего в первом столбце), свести дело к определителю второго порядка. Ко 2-й строке прибавим 1-ю, умноженную на -4, к 3-й - первую, умноженную на 3:

Разлагаем определитель по элементам первого столбца:

И здесь можно упростить вычисления: ко 2-й строке прибавим 1-ю, затем ко 2-му столбцу прибавим 1-й, умноженный на 2:

Замечание. При использовании свойства 8, следует иметь в виду, что в преобразованном определителе меняется только та строка (столбец), к которой прибавляется другая. Так, если, например, к 3-й строке прибавляется 1-я, умноженная на 2, то в преобразованном определителе первая строка останется в неизменном виде, меняется только 3-я строка.