5.4 Резонансный способ измерения частоты

Резонансный способ основывается на сравнении измеряемой частоты с частотой собственных колебаний колебательного контура или резонатора, отсчётные устройства которых предварительно градуируются.

Приборы, измеряющие частоту резонансным методом, называют резонансными частотомерами. Эти простые приборы применяются в частотном диапазоне от килогерц до сотен гигагерц. Основным узлом резонансного частотомера является перестраиваемая по частоте колебательная система. На частотах до сотен мегагерц в качестве колебательной системы применяются резонансные контуры с сосредоточенными постоянными, на более высоких частотах, вплоть до 1 ГГц - контуры с распределенными постоянными в виде отрезков коаксиальной или полосковой линии, на еще более высоких частотах применяются объемные резонаторы.

Применение резонансных частотомеров в диапазоне СВЧ легко объясняется возможностью создания в этом диапазоне высокодобротных колебательных систем с резким проявлением резонанса и его точной фиксацией. Колебательными системами в диапазоне СВЧ являются контуры с распределенными постоянными в виде коаксиальных и волновых резонаторов. Как известно из теории длинных линий, размеры резонаторов, в момент настройки их в резонанс, однозначно связанны с длиной волны возбуждаемых колебаний. Это позволяет определить по результатам измерения искомое значение f_х. В качестве примеров можно рассмотреть РЧ с коаксиальным резонатором (рис.5.5).

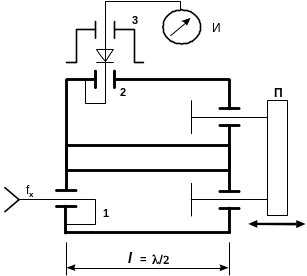
Рисунок 5.5 - Схемотехническое устройство резонансного частотомера СВЧ

Как видно из рис.5.5, коаксиальный резонатор представляет собой отрезок короткозамкнутой коаксиальной линии, длина которого изменяется перемещением поршня П с помощью микрометрического механизма, снабженного соответствующей шкалой.

Связь резонатора с источником сигнала fх и индикатором резонанса - индуктивная, осуществляемая с помощью петель связи 1 и 2. Индикатор резонанса состоит из детекторной камеры 3 с полупроводниковым диодом и индикатора И, в качестве которого при измерении частоты непрерывных сигналов применяют магнитоэлектрические приборы, а при измерении частоты импульсно-модулированных сигналов - селективные измерительные усилители.

Резонанс в такой системе наступает каждый раз, когда  = n * /2, где n = 1, 2, 3, ..., и фиксируется по максимальным показаниям индикатора И. Шкалу перемещения поршня П иногда градуируют в значениях f_x и тогда получается прямоотсчетный РЧ с фиксацией только одного резонанса, или пользуются градуировочными таблицами.

Класс точности таких РЧ определяется как добротностью резонатора, чувствительностью и погрешностью микрометрического механизма П, так и влиянием на РЧ внешних условий - температуры и влажности. Для минимизации этого влияния применяются материалы с малым температурным коэффициентом расширения (ТКР) (например, инвар), температурная компенсация и герметизация резонаторов.

В общем случае основная погрешность измерения резонансным способом может быть записана в виде:

δf_x = δf _обр + δf_гр + 2 δf_нр + δf_отс,

где δf_обр - относительная погрешность образцового прибора, по которому проводилась градуировка; δf_нр - относительная погрешность настройки в резонанс, которая проявляется при градуировке и при измерении; δf_гр - погрешность градуировки, обусловленная неточностью нанесения делений на шкале; δf_отс - погрешность отсчета.

Погрешность градуировки δf_гр и погрешность отсчета δf_отс могут быть сделаны пренебрежимо малыми по сравнению с остальными составляющими.

[1.с.178-200; 2.с.129-139; 3, с.111-118;].