
- •Раздел I механика поступательного и вращательного движения тел
- •1. Кинематика
- •1.1. Основные понятия кинематики
- •1.2. Законы сложения скоростей и ускорений
- •Основы динамики.
- •2.1. Инерциальные системы отсчета. Первый закон Ньютона
- •2.2. Масса. Количество движения. Сила. Второй закон Ньютона. Третий закон Ньютона
- •2.3. Вращательное движение твердого тела.
- •2.4. Момент инерции
- •2.5. Кинетическая энергия движения твердого тела
- •2.6. Теорема Штейнера
- •2.7. Момент количества движения
- •2.9. Второй закон Ньютона для вращательного движения
- •2.10. Гироскоп. Скорость прецессии гироскопа
- •2.11. Закон сохранения массы. Закон сохранения количества движения. Реактивное движение
- •Реактивное движение. Уравнение Циолковского-Мещерского
- •2.12. Закон сохранения момента количества движения
- •2.13. Механическая работа и потенциальная энергия. Типы равновесия
- •2.14. Закон сохранения энергии
- •2.15. Применение законов сохранения. Упругое соударение шаров
- •2.17. Силы трения
- •2.18. Силы тяготения.
- •Ускорение свободного падения
- •Космические скорости
- •2.19. Силы инерции
- •3. Механические колебания и волны
- •3.1. Гармонические колебания
- •3.2. Потенциальная, кинетическая и полная энергии
- •3.3. Пружинный, математический, физический и крутильный маятники
- •3.4. Затухающие колебания
- •3.5. Вынужденные колебания
- •3.6. Параметрический резонанс
- •3.7. Сложение колебаний одинакового направления
- •3.8. Сложение колебаний
- •Негармонические периодические колебательные
- •3.10. Механические волны. Фазовая скорость волны
- •3.11. Фазовая и групповая скорости распространения волн. Дисперсия. Формула Рэлея.
- •3.12. Стоячая волна
- •3.13. Эффект Допплера
- •3.14. Акустические волны
- •Основы гидродинамики и аэродинамики
- •4.1. Уравнение неразрывности струи
- •4.2. Уравнение Бернулли
- •4.3. Течение вязкой жидкости
- •4.4. Сопротивление движению тел в жидкостях
- •4.5. Кинематическая вязкость. Число Рейнольдса
- •4.6. Аэродинамические силы
- •Раздел II молекулярНая физиКа и термодинамика
- •Основные макропараметры
- •1.1. Температура
- •1.2. Давление
- •2. Идеальный газ. Уравнение состояния идеального газа
- •3. Законы Бойля Мариотта, Гей Люссака, Шарля,
- •3.1. Закон Бойля Мариотта
- •3.2. Закон Гей Люссака
- •3.3. Закон Шарля
- •3.4. Закон Дальтона
- •Идеальный газ во внешнем силовом поле.
- •5. Распределение частиц по скоростям при тепловом равновесии. Распределения Максвелла
- •6. Работа при тепловых процессах
- •8. Теплоемкость
- •8.1. Теплоемкость при постоянном давлении и при постоянном объеме
- •8.2. Теплоемкость одноатомного газа
- •8.3. Теплоемкость двухатомного газа
- •8.4. Теплоемкость твердого тела.
- •9. Адиабатический процесс
- •10. Цикл Карно
- •11. Необратимость тепловых процессов
- •12. Второе начало термодинамики. Энтропия
- •Агрегатные состояния вещества. Уравнение Ван дер Ваальса. Фазовые переходы
- •14. Жидкости
- •14.1. Поверхностные явления
- •14.2. Капиллярные явления
- •14.3. Упругость пара над искривленной поверхностью
- •14.5. Кристаллические модификации
- •Фазовые переходы второго рода
- •15. Столкновения молекул и явления переноса
- •Диффузия, теплопроводность,
- •15.2. Средняя длина свободного пробега молекул, среднее время свободного пробега молекул, средняя частота столкновений молекул
- •15.3. Прицельный параметр и эффективное сечение столкновений
- •Коэффициент диффузии
- •15.5. Коэффициент теплопроводности
- •15.6. Теплосопротивление
- •15.7. Внутреннее трение в газах. Вязкость
- •15.8. Свойства газов при низких давлениях
- •Содержание
- •Раздел I. Механика поступательного и вращательного
- •Кинематика . . . . . . . . . . . . . . . . . . . . . . . . . 3
- •1.1. Основные понятия кинематики . . . . . . . . . . . 3
- •Раздел II. Молекулярная физика и термодинамика . . . . . 109
- •117923, Гсп-1, г. Москва, ул. Орджоникидзе, д. 3
- •117923, Гсп-1, г. Москва, ул. Орджоникидзе, д. 3, тел. 952-04-41
Агрегатные состояния вещества. Уравнение Ван дер Ваальса. Фазовые переходы
По мере увеличения плотности газа становится существенным взаимодействие между молекулами. Увеличение давления может сопровождаться превращением газа в жидкость, среду со свойствами существенно отличными от свойств газа, тем более идеального газа.
Эти явления связаны с взаимодействием молекул между собой. Выяснить в деталях характер этого взаимодействия в данном разделе физики не представляется возможным, однако, можно привести факты, а в дальнейшем их использовать, показывающие, что на близких расстояниях молекулы отталкиваются (газ нельзя сжать до бесконечно малого объема, а на больших – притягиваются (жидкость не распадается на молекулы, самопроизвольно не превращается в пар).
Учтем эти силы в уравнение состояния идеального газа:
силы отталкивания не позволяют сжать газ до бесконечно малого объема, поэтому, вместо в уравнении , запишем
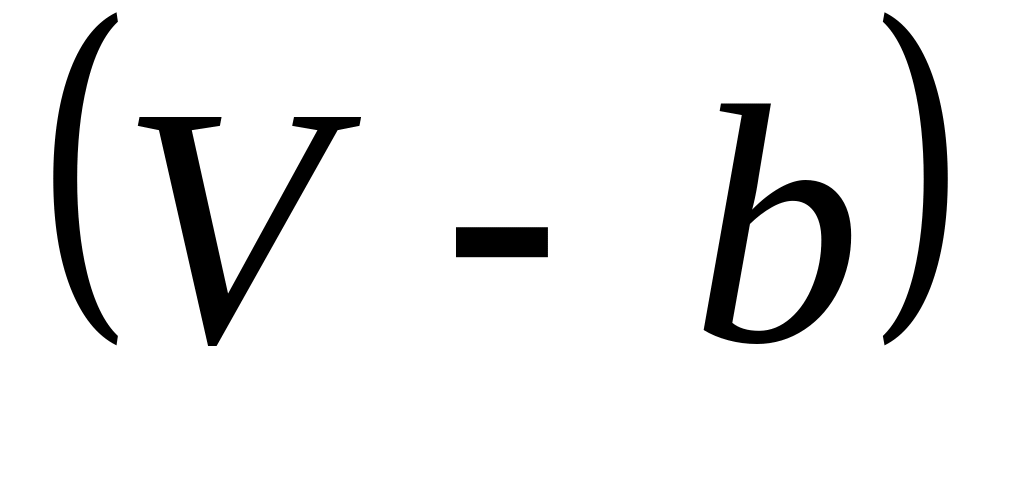 .
При этом получим
.
При этом получим
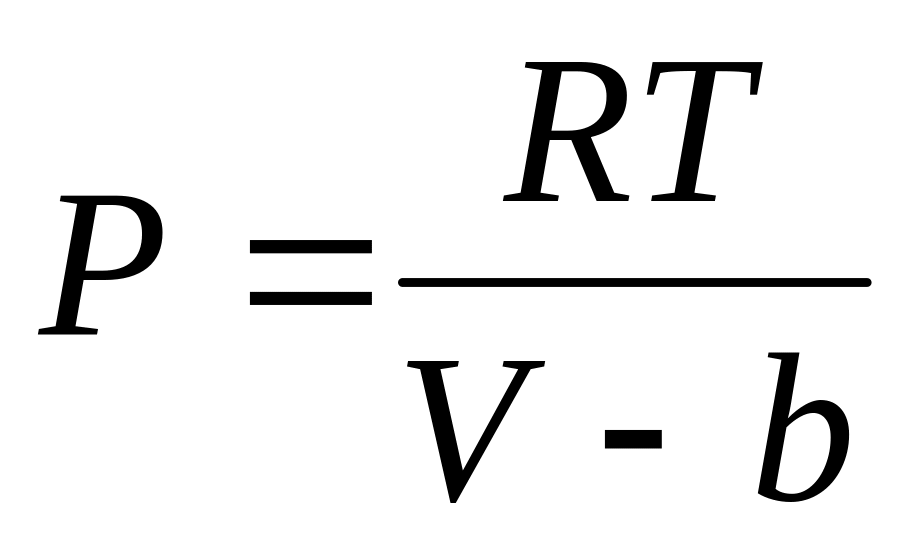 .
Видно, что при
.
Видно, что при

 ,
,силы притяжения уменьшают давление, т.к. они стремятся сжать газ. Поправку к давлению учтем следующим образом. На каждую молекулу действует сила пропорциональная плотности газа ~
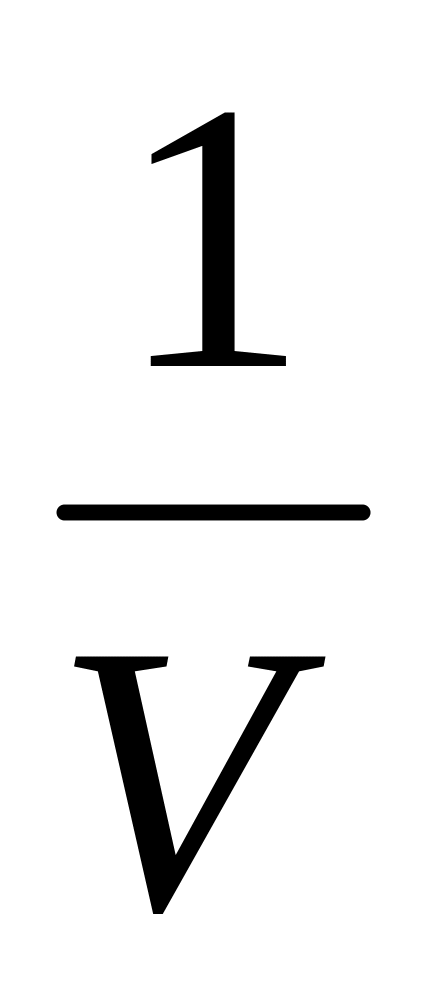 ,
где
-объем,
но давление тем меньше, чем больше
молекул, т.е. опять имеем пропорциональность
.
Таким образом поправка к давлению ~
,
где
-объем,
но давление тем меньше, чем больше
молекул, т.е. опять имеем пропорциональность
.
Таким образом поправка к давлению ~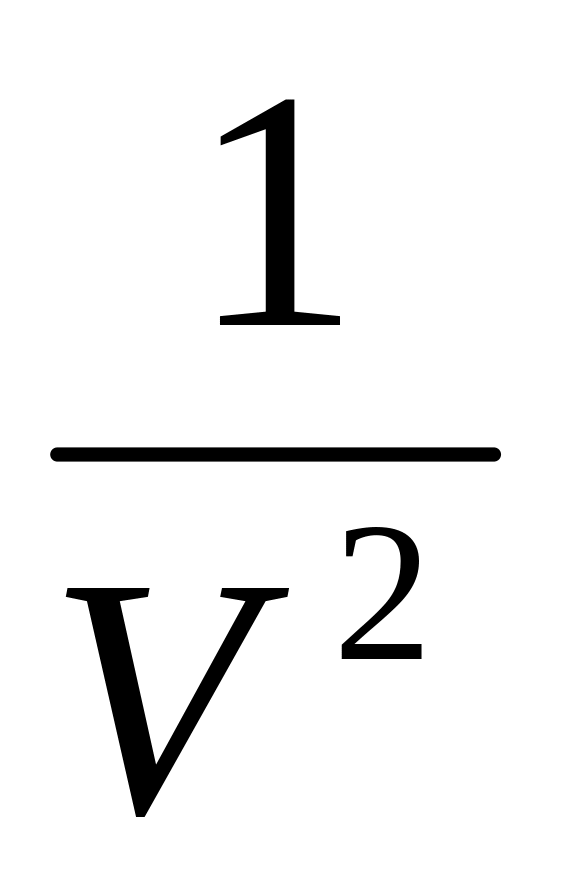 .
Обозначим эту поправку как
.
Обозначим эту поправку как
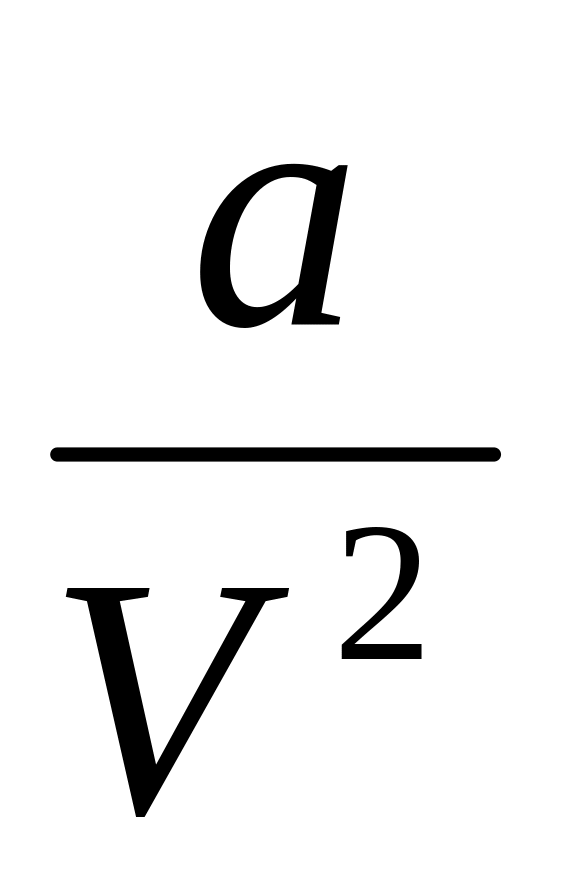 ,
где
-
некоторая константа, характеризующая
силы притяжения молекул. Поэтому имеем:
,
где
-
некоторая константа, характеризующая
силы притяжения молекул. Поэтому имеем:
-
или, для одного моля вещества, получаем:
![]() .
.
Это уравнение состояния реального газа или, как его еще называют, уравнение Ван дер Ваальса. Коэффициенты и называются константами Ван дер Ваальса. Они зависят от типа газа.
При
малых плотностях газа, когда
![]() ,
поправками Ван дер Ваальса можно
пренебречь и получить уравнение состояния
идеального газа.
,
поправками Ван дер Ваальса можно
пренебречь и получить уравнение состояния
идеального газа.
Представим полученное уравнение в виде:
![]() .
.
Это уравнение третей степени, следовательно, оно имеет три корня. Анализ показывает, что отрицательных корней нет, а корни либо все три действительные, либо один действительный и два комплексно сопряженных.
Н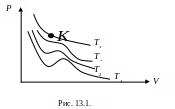 а
-диаграмме
(рис. 13.1) представлены изотермы Ван дер
Ваальса для различных температур:
а
-диаграмме
(рис. 13.1) представлены изотермы Ван дер
Ваальса для различных температур:
![]() .
.
Видим, что при низких температурах изотермы реального газа существенно отличаются от изотермы идеального газа.
Рассмотрим на изотерме реального газа (рис. 13.2) следующие участки:

(a-c) и (e-d) - на этих участках с ростом объема уменьшается давление, что находится в соответствии с экспериментом.
(с-e) – этот участок изотермы на практике не реализуется.
Как показывает опыт реальной изотерме Ван дер Ваальса соответствует кривая (a-b-f-d).
Участок (a-b) соответствует газообразному состоянию, (f-d) – жидкому, горизонтальный участок (b-f) - переходному двухфазовому состоянию вещества, в котором две фазы жидкая и газообразная находятся одновременно. Причем для данного вещества этому переходу соответствует определенное давление, определяемое температурой.
Участки (e-f) и (b-c) отвечают метастабильным состояниям: переохлажденному пару (газу) и перегретой жидкости соответственно.
При
повышении температуры прямолинейный
участок (b-f)
сужается до точки (К). Это критическая
точка (см. рис.13.1). В этой точке при фазовом
переходе объем сохраняется, а производная
![]() .
Температура, при которой это происходит
называется критической (
.
Температура, при которой это происходит
называется критической (![]() ).
При
).
При
![]() -
преобразования фазовых состояний нет,
существует только газообразная фаза.
При
-
преобразования фазовых состояний нет,
существует только газообразная фаза.
При
![]() возможно существование как жидкой, так
и газообразной фаз.
возможно существование как жидкой, так
и газообразной фаз.
Из изотерм Ван дер Ваальса видно, как сделать газ жидкостью. Для этого необходимо охладить газ до температуры ниже критической и потом сжать.
