
- •Раздел I механика поступательного и вращательного движения тел
- •1. Кинематика
- •1.1. Основные понятия кинематики
- •1.2. Законы сложения скоростей и ускорений
- •Основы динамики.
- •2.1. Инерциальные системы отсчета. Первый закон Ньютона
- •2.2. Масса. Количество движения. Сила. Второй закон Ньютона. Третий закон Ньютона
- •2.3. Вращательное движение твердого тела.
- •2.4. Момент инерции
- •2.5. Кинетическая энергия движения твердого тела
- •2.6. Теорема Штейнера
- •2.7. Момент количества движения
- •2.9. Второй закон Ньютона для вращательного движения
- •2.10. Гироскоп. Скорость прецессии гироскопа
- •2.11. Закон сохранения массы. Закон сохранения количества движения. Реактивное движение
- •Реактивное движение. Уравнение Циолковского-Мещерского
- •2.12. Закон сохранения момента количества движения
- •2.13. Механическая работа и потенциальная энергия. Типы равновесия
- •2.14. Закон сохранения энергии
- •2.15. Применение законов сохранения. Упругое соударение шаров
- •2.17. Силы трения
- •2.18. Силы тяготения.
- •Ускорение свободного падения
- •Космические скорости
- •2.19. Силы инерции
- •3. Механические колебания и волны
- •3.1. Гармонические колебания
- •3.2. Потенциальная, кинетическая и полная энергии
- •3.3. Пружинный, математический, физический и крутильный маятники
- •3.4. Затухающие колебания
- •3.5. Вынужденные колебания
- •3.6. Параметрический резонанс
- •3.7. Сложение колебаний одинакового направления
- •3.8. Сложение колебаний
- •Негармонические периодические колебательные
- •3.10. Механические волны. Фазовая скорость волны
- •3.11. Фазовая и групповая скорости распространения волн. Дисперсия. Формула Рэлея.
- •3.12. Стоячая волна
- •3.13. Эффект Допплера
- •3.14. Акустические волны
- •Основы гидродинамики и аэродинамики
- •4.1. Уравнение неразрывности струи
- •4.2. Уравнение Бернулли
- •4.3. Течение вязкой жидкости
- •4.4. Сопротивление движению тел в жидкостях
- •4.5. Кинематическая вязкость. Число Рейнольдса
- •4.6. Аэродинамические силы
- •Раздел II молекулярНая физиКа и термодинамика
- •Основные макропараметры
- •1.1. Температура
- •1.2. Давление
- •2. Идеальный газ. Уравнение состояния идеального газа
- •3. Законы Бойля Мариотта, Гей Люссака, Шарля,
- •3.1. Закон Бойля Мариотта
- •3.2. Закон Гей Люссака
- •3.3. Закон Шарля
- •3.4. Закон Дальтона
- •Идеальный газ во внешнем силовом поле.
- •5. Распределение частиц по скоростям при тепловом равновесии. Распределения Максвелла
- •6. Работа при тепловых процессах
- •8. Теплоемкость
- •8.1. Теплоемкость при постоянном давлении и при постоянном объеме
- •8.2. Теплоемкость одноатомного газа
- •8.3. Теплоемкость двухатомного газа
- •8.4. Теплоемкость твердого тела.
- •9. Адиабатический процесс
- •10. Цикл Карно
- •11. Необратимость тепловых процессов
- •12. Второе начало термодинамики. Энтропия
- •Агрегатные состояния вещества. Уравнение Ван дер Ваальса. Фазовые переходы
- •14. Жидкости
- •14.1. Поверхностные явления
- •14.2. Капиллярные явления
- •14.3. Упругость пара над искривленной поверхностью
- •14.5. Кристаллические модификации
- •Фазовые переходы второго рода
- •15. Столкновения молекул и явления переноса
- •Диффузия, теплопроводность,
- •15.2. Средняя длина свободного пробега молекул, среднее время свободного пробега молекул, средняя частота столкновений молекул
- •15.3. Прицельный параметр и эффективное сечение столкновений
- •Коэффициент диффузии
- •15.5. Коэффициент теплопроводности
- •15.6. Теплосопротивление
- •15.7. Внутреннее трение в газах. Вязкость
- •15.8. Свойства газов при низких давлениях
- •Содержание
- •Раздел I. Механика поступательного и вращательного
- •Кинематика . . . . . . . . . . . . . . . . . . . . . . . . . 3
- •1.1. Основные понятия кинематики . . . . . . . . . . . 3
- •Раздел II. Молекулярная физика и термодинамика . . . . . 109
- •117923, Гсп-1, г. Москва, ул. Орджоникидзе, д. 3
- •117923, Гсп-1, г. Москва, ул. Орджоникидзе, д. 3, тел. 952-04-41
4.4. Сопротивление движению тел в жидкостях
Выше были представлены простейшие законы движения жидкости (газа). Теперь рассмотрим особенности движения тел в жидкостях (газах).
Как установил Стокс, на тело шарообразной формы, движущееся с небольшой скоростью в жидкости, действует сила сопротивления, равная
![]() ,
,
где - коэффициент вязкости,
- радиус шарика,
- его скорость движения.
Эта формула часто
используется для расчета стационарной
скорости падения шарообразного тела в
вязкой среде (![]() ).
Определим эту скорость. При равномерном
движении тел все действующие на него
силы уравновешивают друг друга. Для
рассматриваемого случая
).
Определим эту скорость. При равномерном
движении тел все действующие на него
силы уравновешивают друг друга. Для
рассматриваемого случая
![]() ,
,
где
![]() – сила тяжести,
– сила тяжести,
- плотность материала шарика,
![]() -
сила вязкого трения Стокса,
-
сила вязкого трения Стокса,
![]() - сила Архимеда,
- сила Архимеда,
![]() - плотность среды.
- плотность среды.
Решение этого уравнения относительно имеет вид:
![]() .
.
Более детальное рассмотрение этой задачи, позволяет найти динамику движения тела сферической формы в вязкой среде. В соответствии со вторым законом Ньютона, предполагая, что движение происходит в направлении оси , запишем:
![]() .
.
Это уравнение может быть преобразовано к виду:
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() .
.
Решением выше представленного уравнения является:
![]() .
.
Величина постоянной
интегрирования находится из условия,
что в начальный момент времени скорость
тела была равной
,
поэтому
![]() .
.
В результате получаем:
![]()
или
![]() .
.
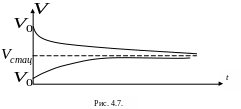
Анализ представленного решения показывает, что в зависимости от начальных условий, соотношения плотностей материалов шарика и среды движение тела будет различным. На рис. 4.7 представлен характер изменения скорости шарообразного тела, плотность которого выше плотности среды, для двух значений начальной скорости.
При больших
скоростях
движения тел в жидкостях или газах
возникают завихрения, энергия затрачивается
на их образование при этом сила
сопротивления становится пропорциональной
![]() и площади сечения тела
,
перпендикулярной скорости движения.
Для этого случая Ньютоном была получена
формула для силы трения, которая имеет
вид:
и площади сечения тела
,
перпендикулярной скорости движения.
Для этого случая Ньютоном была получена
формула для силы трения, которая имеет
вид:
![]() ,
,
где
![]() - плотность среды,
- плотность среды,
![]() -
коэффициент лобового сопротивления,
который зависит от формы тела, определяющей
характер вихрей:
-
коэффициент лобового сопротивления,
который зависит от формы тела, определяющей
характер вихрей:
-
квадратная пластинка, перпендикулярная
потоку газа (жидкости).
![]() ,
,
-
диск, перпендикулярный потоку газа
(жидкости).
![]() ,
,
-
шар,
![]() ,
,
-
сигарообразное тело (длина = 4 диаметрам).
![]() .
.
Физический смысл
формулы Ньютона состоит в том, что тело,
при своем движении, оттесняет за 1 секунду
массу жидкости (газа), равную
![]() .
Скорость, сообщаемая телом частицам
оттесненной среды, в среднем равна
скорости самого тела, поэтому, количество
движения, теряемое телом за одну секунду,
будет равно
.
Скорость, сообщаемая телом частицам
оттесненной среды, в среднем равна
скорости самого тела, поэтому, количество
движения, теряемое телом за одну секунду,
будет равно
![]() .
Эта величина определяет возникающую
силу сопротивления движению, силу,
обусловленную инерционными свойствами
частиц среды.
.
Эта величина определяет возникающую
силу сопротивления движению, силу,
обусловленную инерционными свойствами
частиц среды.
4.5. Кинематическая вязкость. Число Рейнольдса
Опыт подтверждает представленные выше выражения для сил сопротивления движению тел в вязких средах, а именно, то, что при малых скоростях сила трения пропорциональна скорости движения тела, а при больших – квадрату ее величины.
Если предположить,
что формула Ньютона более универсальна,
чем формула Стокса, то следует
констатировать, что значение
является функцией
![]() ,
где
-
характерный размер тела, причем их
комбинация должна быть безразмерной.
Такой комбинацией является величина:
,
где
-
характерный размер тела, причем их
комбинация должна быть безразмерной.
Такой комбинацией является величина:
![]() ,
,
называемая
числом
Рейнольдса.
(![]() ).
).
Число Рейнольдса
имеет важный физический смысл. Оно
пропорционально отношению силы трения,
связанной с инерционными свойствами
частиц среды (~
![]() ),
к силе трения, обусловленной вязкостью
среды (
),
к силе трения, обусловленной вязкостью
среды (![]() ).
).
Величина
![]() называется кинематической
вязкостью.
называется кинематической
вязкостью.
![]() .
.
Из представленных в таблице значений видно,
Среда |
Кинематическая
вязкость ( |
Вода при 20
|
O,01 |
Воздух при 20 |
0,15 |
Воздух при 0 , (7 Тор) |
13,3 |
Глицирин при 20 |
6,8 |
что кинематическая вязкость воды может быть меньше кинематической вязкости воздуха – это следствие того, что плотность воздуха меньше плотности воды.
Число Рейнольдса
– главная характеристика обтекаемости
тел. При малых значениях
![]() - течение имеет ламинарный характер,
при больших – турбулентный.
- течение имеет ламинарный характер,
при больших – турбулентный.
При моделировании потоков (строительство каналов, различных гидросооружений и т.д.) проводят макетирование, при этом важно не только повторить геометрию, но и реализовать в эксперименте соответствующее реальности .
