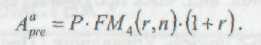6.2.4. Визначення вартості грошей у часі

Відомо, що гроші — це особливий товар, який можна обміню­вати на будь-які інші товари без обмежень. Крім того, гроші — це еквівалент вартості всіх інших товарів, оскільки саме за допомогою грошей у вигляді фіксованої їх кількості вимірюється вар­тість будь-якого товару.

Однак самі гроші мають вартість. Причому грошова одиниця, яка є сьогодні, і грошова одиниця, яка очікується до одержання через деякий час, не є рівноцінними: мати певну суму грошей сьогодні завжди краще, ніж мати її завтра (принцип діє незалеж­но від зміни загального рівня цін). Це пояснюється впливом трьох основних факторів (рис. 6.6).

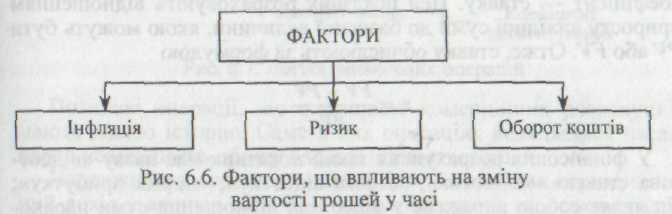
Інфляція — явище, властиве практично будь-якій економіці, наслідком якого є знецінення грошей. Якщо уявити, що підпри­ємство має вільні грошові кошти у розмірі 300 000 грн, а темп інфляції на рік становить 20 %, то вже в наступному році, якщо гроші не використовувалися, а зберігалися, їх купівельна спромож­ність знизиться і реальна вартість дорівнюватиме 240 000 грн.

Ризик неодержання очікуваної суми також є достатньо очевид­ною причиною. Будь-який договір, згідно з яким очікується над­ходження грошових коштів у майбутньому, має ненульову ймо­вірність бути невиконаним узагалі або виконаним частково.

Оборот коштів — фактор, який полягає в тому, що кошти, як і будь-який актив, повинні з часом генерувати дохід за ставкою, яка задовольняє власника. Тому сума, очікувана до одержання через деякий час, має перевищувати початкову суму, якою воло­діє інвестор у момент прийняття рішення, на величину можливо­го доходу.

У будь-якому разі вартість однієї й тієї самої суми грошей сьогодні завжди є більшою, ніж завтра, оскільки вимірювання вар­тості грошей ґрунтується на можливості їх використання протя­гом певного періоду часу.

Саме на основі розрахунку вартості використання грошей протягом певного періоду часу ґрунтуються концепції майбут­ньої та теперішньої їх вартості, алгоритм визначення якої полягає в такому.

Найпростішим видом фінансової угоди є одноразове надання в борг певної суми РV з умовою, що через деякий час t буде по­вернена більша сума FV. Як відомо, результативність подібної угоди може бути охарактеризована двояко: або за допомогою аб­солютного показника — FV - РV, або розрахунком певного від­носного показника. Абсолютні показники частіше за все не під­ходять для подібної оцінки у зв'язку з їх незрівнянністю в просторово-часовому аспекті. Тому використовують спеціальний коефіцієнт — ставку. Цей показник розраховують відношенням приросту вихідної суми до базисної величини, якою можуть бути РV або FV. Отже, ставку обчислюють за формулою

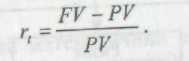
У фінансових розрахунках такий показник має назву «відсот­кова ставка», «відсоток», «ставка відсотку», «норма прибутку»; він являє собою виражене у відсотках відношення суми нарахо­ваного за певний інтервал доходу до суми, що є на початок дано­го інтервалу.

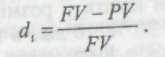
Визначену так відсоткову ставку називають обліковою, або дисконтом. Цей показник розраховують як відношення суми до­ходу, що виплачується за певний інтервал, до величини нароще­ної суми, одержаної по закінченні цього інтервалу.

Очевидно, що обидві ставки взаємозв'язані, тобто знаючи один показник, можна розрахувати інший:

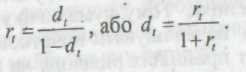
У будь-якій простій фінансовій угоді завжди присутні три ве­личини, дві з яких задані, а одна є шуканою.

Процес, в якому задані вихідна сума і відсоткова ставка, у фі­нансових розрахунках має назву нарощення. Процес, в якому за­дані очікувана в майбутньому до отримання сума і коефіцієнт дисконтування, називають процесом дисконтування. У першому випадку йдеться про рух грошових потоків від сучасного до май­бутнього, у другому — про рух від майбутнього до сучасного (рис. 6.7).

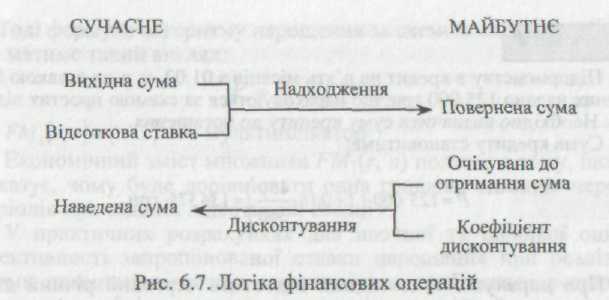
Позикові операції, що є основою комерційних розрахунків, мають давню історію. Саме в цих операціях виявляється насам­перед необхідність обліку часової цінності грошей.

Надаючи свої грошові кошти в борг, їх власник отримує пев­ний дохід у вигляді відсотків, які нараховують по деякому алго­ритму протягом певного проміжку часу. Оскільки стандартним часовим інтервалом у фінансових операціях є один рік, найбільш поширеним варіантом є встановлення відсоткової ставки у вигля­ді річної ставки, яка передбачає одноразове нарахування відсот­ків після закінчення року з моменту отримання позики.

Відомі дві основні схеми нарахування відсотків: проста і складна.

Схема нарахування простих відсотків припускає незмін­ність бази, з якої відбувається нарахування. Якщо на початку ро­ку інвестор розміщує на рахунку в банку суму Р під відсоток r, то через п років вкладник одержить:

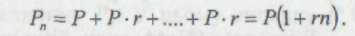
Приклад З

Визначити нарощену суму з вихідної суми в 4000 грн при розмі­щенні її в банку на умовах нарахування простих відсотків, якщо річна ставка — 13%, а період нарахування — 15 років.

Нарощена сума становитиме:

4000 (1 + 15*0,13) =11 800 грн.

Якщо простий відсоток нараховують протягом періоду, який менший за рік, то попередня формула трансформується в таку:

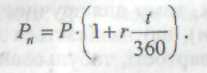
Приклад 4

Підприємству в кредит на п^’ять місяців з 01.02. ц. з. за ставкою 18 % річних надано 125 000 грн, що нараховуються за схемою простих відсот­ків. Необхідно визначити суму кредиту до погашення.

Сума кредиту становитиме:

При нарахуванні складних відсотків черговий річний дохід визначають не з вихідної величини інвестованого капіталу, а із загальної суми, яка включає також раніше нараховані, але незатребувані інвестором відсотки. У цьому разі відбувається капіта­лізація відсотків у міру їх нарахування.

Відповідно до ідеології нарахування складних відсотків у кін­ці першого року розмір інвестованого капіталу дорівнюватиме: Р1 =Р + Р*r = Р*(1 + г); у кінці

другого: Р₂ = Р₁ + Р₁*r = Р_r (1 + г) = Р * (1 + r)²; у кінці n-го року: Р_п = Р * (1 + r)".

Приклад 5

На внесок у банк у розмірі 8500 грн строком на шість років нарахо­вується 15 % річних за схемою складних відсотків. Яка сума буде на рахунку в кінці означеного періоду, якщо нарахування відсотків здійс­нюється щокварталу?

Розрахунок буде таким:

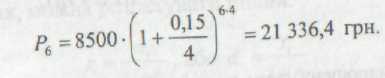
Використання в розрахунках складних відсотків у разі багато­разового його нарахування більш логічно, оскільки в цьому ви­падку капітал, що генерує доходи, постійно зростає. При застосу­ванні простого відсотка доходи в міру їх нарахування доцільно знімати для споживання або використання в інших інвестиційних проектах чи поточній діяльності.

Формула складних відсотків є однією з базових формул у фі­нансових розрахунках, тому для зручності користування значен­ня множника FМ1{r, n), що називається мультиплікатором і за­безпечує нарощення вартості, табульовані для різних значень r і п. Тоді формула алгоритму нарощення за схемою складних відсот­ків матиме такий вигляд:

де FM1 (r,n) = (1+r) —мультиплікатор

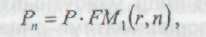
Економічний зміст множника FM1 (r,n) полягає в тому, що він показує, чому буде дорівнювати одна грошова одиниця через п періодів при заданій відсотковій ставці r.

У практичних розрахунках для наочної та швидкої оцінки ефективності запропонованої ставки нарощення при реалізації схеми складних відсотків користуються приблизним розрахун­ком часу, необхідного для подвоєння інвестиційної суми, відомо­го як «правило 72-х». Це правило передбачає, що якщо r — від­соткова ставка, то к = 72/r являє собою кількість періодів, за яке вихідна сума збільшиться приблизно вдвічі.

Таке правило добре спрацьовує для невеликих значень r (до 20%). Так, якщо річна ставка r- 12 %, то к~ 72 /12 = 6.

Оцінюючи доцільність фінансових вкладень у той чи інший вид бізнесу, виходять з того, що визначають прибутковість цих вкладень. Завдання зводиться до того, щоб порівняти інвестиції, які підприємець має зробити сьогодні, із грошових надходжень, які він отримає в майбутньому. Тобто виникає необхідність порів­няння сум грошей у різні моменти часу. Для цього їх приводять до одного часового знаменника — до теперішнього часу.

Основна ідея цієї процедури полягає в тому, щоб оцінити майбутні грошові надходження з позиції поточного моменту, тобто визначити величину суми Р, яка в майбутньому має стано­вити задану величину Р_п. У цьому випадку Р буде відповідати поточній (теперішній, приведеній) вартості Р_п.

Теперішня вартість — грошова вартість майбутніх доходів на теперішній час. Розрахунки теперішньої вартості здійснюють іа допомогою дисконтування.

Дисконтування — це зведення економічних показників різ­них років до порівняльного в часі виду. Дисконтування здійсню­ють за допомогою формули

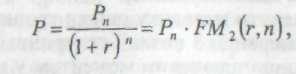
де Рn — майбутня вартість; Р — поточна вартість; 1 / (1 + r)ⁿ — коефіцієнт дисконтування.

Значення коефіцієнта дисконтування табульовані, а його еко­номічний зміст полягає в тому, що він відображує теперішню ці­ну однієї грошової одиниці майбутнього, тобто чому з позиції поточного моменту дорівнюватиме одна грошова одиниця, що циркулює у сфері бізнесу п періодів з моменту розрахунку при заданій відсотковій ставці г та частоті нарахування відсотків.

Приклад 6

Визначити поточну вартість облігації з нульовим купоном номіналь­ною вартістю 5000 грн і строком погашення 12 років, якщо прийнятна норма прибутку становить 14 %.

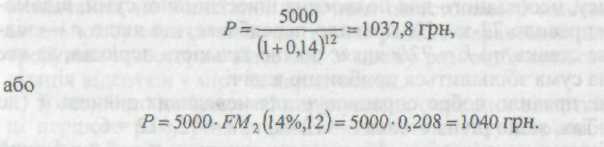
Одним із основних елементів фінансового аналізу є оцінка грошового потоку С1, С2, ..., Сn, що генерується протягом низки часових періодів у результаті реалізації будь-якого проекту. Еле­менти потоку Сn можуть бути або незалежними, або пов'язаними між собою певним алгоритмом. Часові періоди найчастіше пе­редбачаються однаковими. Крім того, для простоти викладення матеріалу передбачено, що елементи грошового потоку є одно-спрямованими, тобто немає чергування відтоку і притоку грошо­вих коштів. Вважають, що надходження, які генеруються в ме­жах одного часового періоду, мають місце або на його початку, або в кінці. У першому випадку потік називають пренумерандо, у другому — постнумерандо.

Крім того, слід знати, що оцінка грошового потоку може ви­конуватися в межах вирішення двох завдань:

а) прямого, коли проводиться оцінка з позиції майбутнього (реалізується схема нарощення);

б) зворотного, коли проводиться оцінка з позиції сучасного (реалізується схема дисконтування).

Перш ніж розглянути методику оцінки грошових потоків пост­нумерандо і пренумерандо з позиції теперішнього та майбутньо­го, слід зауважити, що ключовим моментом у названих схемах є передумова про те, що аналіз здійснюється з позиції такого інвес­тора, який не накопичує отримані грошові кошти, а негайно інвес­тує їх з метою отримання додаткового доходу.

Розглянемо найбільш поширену ситуацію, коли грошові над­ходження по роках змінюються. Нехай С1, С2, ..., Сn — грошовий потік; r — коефіцієнт дисконтування. Необхідно визначити вар­тість даного грошового потоку з позиції майбутнього й сучасного.

Для прямого завдання майбутню вартість грошового потоку пренумерандо Spre розраховують за формулою

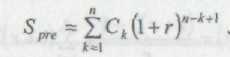
Якщо оцінюється потік постнумерандо, то майбутню його вар­тість визначають як суму нарощених надходжень за формулою:

Зворотне завдання, яке передбачає оцінку з позиції поточного моменту, для грошового потоку постнумерандо виконують за до­помогою формули

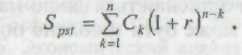
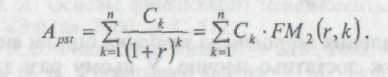
Наведена вартість потоку пренумерандо в загальному виді може бути розрахована за формулою

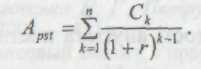
Потік, в якому грошові надходження в кожному періоді од­накові за величиною, називають ануїтетом. Як і в загальному випадку, виділяють два типи ануїтетів: постнумерандо і пре­нумерандо.

Прикладом ануїтета постнумерандо можуть слугувати рент­ні платежі, що регулярно надходять за користування земель­ною ділянкою, зданою в оренду, якщо договором передбачена регулярна оплата оренди по закінченні чергового періоду. Ануїтетом пренумерандо може виступати, наприклад, схема періодичних грошових внесків на банківський рахунок на по­чатку кожного місяця з метою накопичення достатньої суми для великої купівлі.

Пряме завдання оцінки ануїтета при заданих величинах регу­лярного надходження Р і відсотковій ставці r передбачає оцінку майбутньої вартості, і для ануїтета постнумерандо вирішується за допомогою формули:

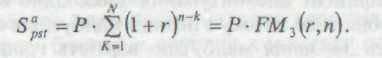
Економічний зміст мультиплікатора

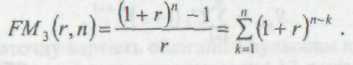
полягає в тому, що він показує, чому дорівнюватиме сумарна ве­личина ануїтета в одну грошову одиницю до кінця строку його дії. Передбачається, що здійснюється лише нарахування грошо­вих сум, а їх вилучення може бути зроблено по закінченні строку дії ануїтетів.

Відповідна розрахункова формула для ануїтета пренумерандо має вигляд

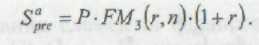
Загальне ставлення зворотного завдання оцінки ануїтета пост­нумерандо також достатньо наочне. У цьому разі здійснюється оцінка майбутніх грошових надходжень з позиції поточного мо­менту, під яким у даному випадку розуміють момент часу, з яко­го починають відраховуватися однакові часові інтервали, що входять до ануїтета.

Оцінку поточної вартості ануїтета постнумерандо розрахову­ють за формулою:

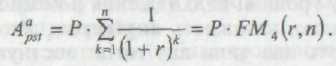
Економічний зміст коефіцієнта дисконтування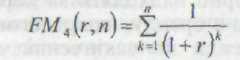

полягає в тому, що він показує, чому дорівнює з позиції поточно­го моменту величина ануїтета з регулярними грошовими надходженнями в розмірі однієї грошової одиниці, яке продовжується п рівних періодів із заданою відсотковою ставкою r.

Відповідна розрахункова формула для ануїтета пренумерандо така: