23

Федеральное агентство связи

Московский технический университет связи и информатики

Кафедра технической электродинамики и антенн

Анализ Электромагнитного поля в прямоугольном волноводе

Проверил: доцент кафедры Выполнил: студент группы РС технической электродинамики и . антенн Муравцов А.Д.

Москва 2008

Задача № 1-4

В полой трубе прямоугольного сечения (см. рис. 1) создано монохроматическое электромагнитное поле. Труба заполнена однородной изотропной средой без потерь, абсолютны диэлектрическая и магнитная проницаемости равны и соответственно. Известно, что комплексная амплитуда вектора равна:

, где

, ,

, , , - частота электромагниных колебаний; - длина волны, распространяющейся в однородной изотропной непроводящей среде с параметрами и ; - скорость света в этой среде, .

Исходные данные:

№ вар	В/м			a см	b см		ГГц	ГГц
2	100	2	1	5	3	0,75	6	2,5

Рис.1

1. Найдем комплексные амплитуды составляющих вектора .

Запишем выражения для комплексных амплитуд составляющих вектора

(1)

(2)

(3)

Воспользуемся вторым уравнением Максвелла в комплексной форме:

(4)

Найдем

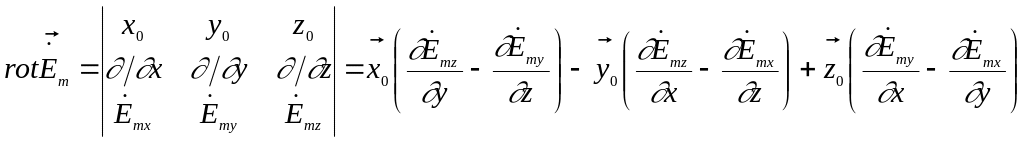
Тогда составляющие комплексной амплитуды вектора равны соответственно:

Найдем выражения для частных производных составляющих комлекной амлитуды вектора по соответствующим координатам:

, так как продольная составляющая вектора отсутствует.

Подставим полученные выражения в выражения для составляющих вектора , полученные ранее:

(5)

(6)

(7)

Упростив варыжения (5), (6), (7), получим итоговые выражения для коплексных амплитуд составляющих вектора

(8)

(9)

(10)

2. Определим диапопзон частот в котором – действительное число, т.Е. Рассматриваемое поле – бегущая волна.

По условию задачи . Значит, будет действительным в случае, если

, т.е. при см.

Этому диапозону длин волн соответствует диапозон частот:

, где Гц

Если частота волны не принадлежит рассчитанному диапозону частот, то является мнимой величиной. Для этого случая произведем замену: , для учета того факта, при этом ,

3. Запишем выражения для мгновенных значений составляющих векторов поля и для двух случаев:

а) когда принадлежит найденному в п. 2 диапозону частот,

б) когда не принадлежит этому диапозону.

Для получения выражений для мгновенных значений составляющих векторов поля необходимо домножить их комплексные амплитуды на выражение и, выделить действительную часть.

В первом случае выражения для комплексных амлитуд составляющих используются без изменений. Во втором случае необходимо произвести замену, описанную в пункте 2.

Тогда для случая а) получим выражения:

а для случая б) выражения будут иметь вид:

4. Построим графики амплитуд составляющих векторов поля в сечении z=z₀ от координаты x при y=0,25b в интервале и от коожинаты y при x=0,75a в интервале , а также зависимоcти тех же составляющих от координаты z вдоль линии x=0,25a; y=0,25b в интервале на частотах и (см. исходные данные).

Для наглядности построений вычислим соответствующие постоянные множители в выражениях для амплитуд составляющих веторов поля для каждого вида зависимости в отдельности. Для этого подставим соответствующие значения постоянных величин в данные выражения:

1. z=z₀; y=0,25b; ;

, В/м

, В/м

, В/м

, А/м

, А/м

, А/м

2. z=z₀; y=0,25b; ;

, В/м

, В/м

, В/м

, А/м

, А/м

, А/м

3. z=z₀; x=0,75a; ;

, В/м

, В/м

, В/м

, А/м

, А/м

, А/м

4. z=z₀; x=0,75a; ;

, В/м

, В/м

, В/м

, А/м

, А/м

, А/м

5. x=0,25a; y=0,25b; ;

, В/м

, В/м

, В/м

, А/м

, А/м

, А/м

6. x=0,25a; y=0,25b; ;

, В/м

, В/м

, В/м

, А/м

, А/м

, А/м

В выражениях пп. 1, 3, 5 м, рад/с, z₀=0.036 м, , а в пп. 2, 4, 6 м, рад/с, z₀=0.044 м и Нп/м.

Зависимости, рассчитанные в данном пункте работы, были запрограммированы в математическом пакете MathCad 13, где был проведен поточечный расчет и построение соответствующих графиков, приведенных на рис. 2-13.

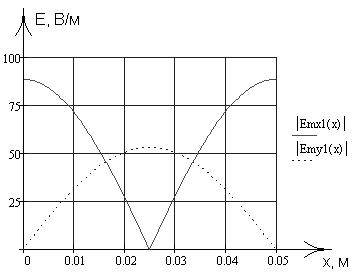
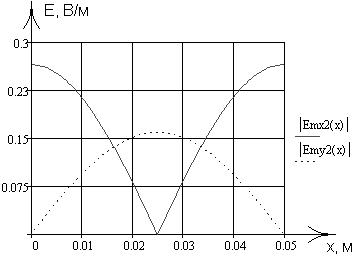
рис. 2 рис. 3

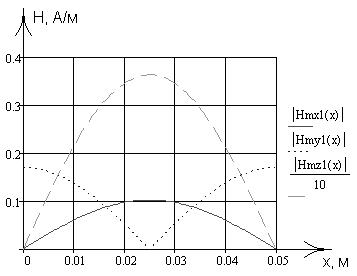
рис. 4 рис. 5

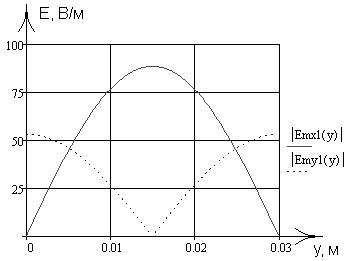
рис. 6 рис. 7

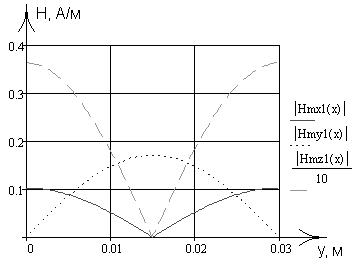
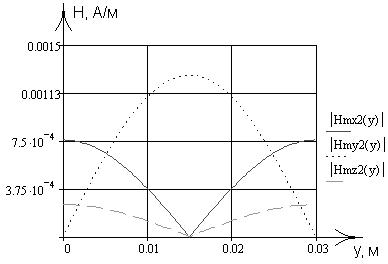
рис. 8 рис. 9

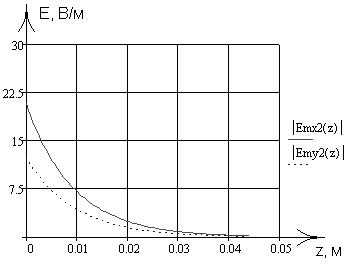
рис. 10 рис. 11

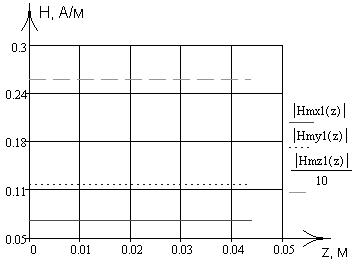
рис. 12 рис. 13

5. Проверим выполнение граничных условий для касательных составляющих вектора и нормальных составляющих вектора на боковой (х=а) и нижней (у=0) стенке трубы.

Проверка граничных условий заключается в проверке истинности утверждений и , т.е. равенста нулю касательной вектора и нормальной вектора проекций (составляющих).

На боковой стенке (х=а) рассмотрению подлежат следующие составляющие:

,

Подставим в эти выражения х=а, получим:

,

при этом другие множители от координаты х не зависят.

Следовательно, оба выражения обращаются в ноль и граничные условия выполняются.

На нижней стенке волновода (y=0) рассмотрим:

,

При подстановке у=0 в эти выражения получим:

Заметим, что на двух оставшихся стенках волновода соответствующие рассмотренные составляющие также обращаются в ноль, так противоположные стенки волновода праллельны.