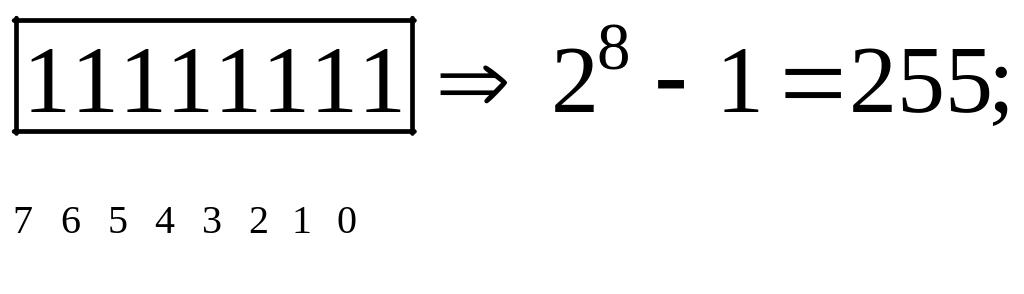- •Простыя даныя мовы Pascal і работа з імі Тыпы звестак
- •Канстанты і пераменныя
- •Абсалютныя пераменныя
- •Цэлалікавыя даныя
- •Бітавая арыфметыка
- •Дзеянні бітавай арыфметыкі
- •Сапраўдныя даныя
- •Аперацыі над сапраўднымі данымі
- •Выразы мовы
- •Літарныя даныя
- •Функцыі
- •Булеўскія даныя
- •Даныя адраснага тыпу
- •Даныя карыстальніцкага тыпу
- •Даныя пералічальнага тыпу
- •Даныя інтэрвальнага тыпу
- •Элементарныя сродкі па рабоце з данымі Наданне значэння даным
Бітавая арыфметыка
Бітавая, або паразрадная, арыфметыка добра развіта ў мове Pascal. Неабходнасць у ёй узнікае, калі трэба працаваць не з дзесятковымі значэннямі лікаў, а з іх двайковым уяўленнем. Бітавыя аперацыі дазваляюць параўноўваць асобныя біты двух лікаў, вылучаць асобныя фрагменты ў ліку, замяняць іх.
Бітавыя аперацыі над сапраўднымі лікамі не прымяняюцца. Яны прымяняюцца толькі над цэлымі тыпамі – Byte, Shortint, Word, Integer, Longint.
Агульная формула для значэнняў даных бяззнакавых тыпаў Byte (1 байт) і Word (2 байты) мае наступны выгляд:
Byte:
значэнне
![]() ;
;
Word:
значэнне
![]() .
.
Значэнні
разрадаў
![]() ,
,
![]() ,
..., роўныя або 0, або
1, адпаведна множацца
на вагу разраду. Адсюль атрымліваем
дыяпазон уяўлення:
,
..., роўныя або 0, або
1, адпаведна множацца
на вагу разраду. Адсюль атрымліваем
дыяпазон уяўлення:
Byte:
Word:
Унутранае адрозненне маюць уяўленні цэлых тыпаў са знакамі Shortint, Integer, Longint. Самы левы біт адводзіцца пад знак, для адмоўнага ліку ён роўны 1, для дадатнага – 0.
Можна запомніць формулу перакладу з 2-й с/зл у іншую сістэму злічэння для тыпаў Shortint (1 байт), Integer (2 байты), Longint (4 байты):
Shortint:
значэнне
![]() ;
;
Integer:
значэнне
![]() ;
;
Longint:
значэнне
![]() .
.
Адсюль дыяпазон уяўлення лікаў:
а) дадатныя Integer (2 байты):
![]()
б) адмоўныя Integer (2 байты) (найменшае атрымаем, калі нічога не будзем дадаваць):
![]()
в) дадатныя Shortint (1 байт):
![]()
г) адмоўныя Shortint (1 байт):
![]()
Дзеянні бітавай арыфметыкі
Першая група паразраднай арыфметыкі – гэта лагічныя аперацыі над бітамі.
Аперацыі |
Назва |
Форма запісу |
Прыярытэт |
Тып |
NOT |
Паразраднае адмаўленне |
NOT A |
1 (вышэйшы) |
Унарны |
AND |
Лагічнае множанне (і) |
A1 AND A2 |
2 |
Бінарны |
OR |
Лагічнае складанне (ці) |
A1 OR A2 |
3 |
|
XOR |
Якая выключае «ці» |
A1 XOR A2 |
4 (ніжэйшы) |
NOT – паразраднае адмаўленне – «пераварочвае» значэнне кожнага біта на процілеглае.
Прыклад. Няхай A = 01101100. Тады NOT A = 10010011.
AND, OR, XOR – лагічныя аперацыі, выконваюцца паразрадна ў адпаведнасці з наступнай табліцай тоеснасці.
A |
B |
A AND B |
A OR B |
A XOR B |
A XOR B XOR B |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
Прыклад.
Няхай
![]() ,
і X,
Y –
пераменныя
тыпу
Shortint.
Пакажам, што
,
і X,
Y –
пераменныя
тыпу
Shortint.
Пакажам, што
![]() .
.
Рашэнне:
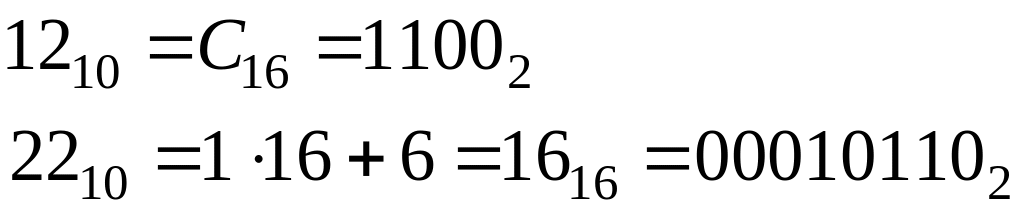

Заўвага. Аперацыя AND у 99 % выпадкаў патрэбна для дзвюх мэт: 1) праверыць наяўнасць канкрэтных бітаў ці 2) зануліць некаторыя з іх.
Калі выконваецца ўмова (X and 32) = 32, тады ў пятым біце пераменнай Х ёсць адзінка (адзінка ў пятым біце дае лік 25 = 32).
Можна праверыць наяўнасць адразу некалькіх уключаных бітаў, напрыклад пятага, другога і нулявога. Атрымаем лік 25 + 22 + 20 = 37. Калі (X and 37) = 37, то так яно і ёсць.
Калі трэба зануліць (выключыць) нейкі біт у пераменнай, тады трэба падрыхтаваць лік, у якім гэты біт нулявы:
![]() – выключылі трэці біт, бо 8 = 23;
– выключылі трэці біт, бо 8 = 23;
![]() – выключылі трэці і сёмы
біты,
бо 23 = 8,
27 = 128.
– выключылі трэці і сёмы
біты,
бо 23 = 8,
27 = 128.
Лагічнае складанне
OR
з поспехам выкарыстоўваецца пры ўстаноўцы
ў значэнне 1 (уключэнні) асобных
бітаў двайковага ўяўлення цэлых лікаў:
![]() – уключылі чацвёрты,
першы
і нулявы
біты, бо 24 = 16, 21 = 2,
20 = 1.
– уключылі чацвёрты,
першы
і нулявы
біты, бо 24 = 16, 21 = 2,
20 = 1.
XOR, якое выключае «ці» (або параўнанне па модулі 2), зварочвае 0, калі абодва аргументы роўныя, і 1 – калі не.
Наступная група паразрадных аперацый – цыклічныя зрухі.
Аперацыя |
Назва |
Форма запісу |
shl |
Цыклічны зрух на N пазіцый улева (l) |
A shl N |
shr |
Цыклічны зрух на N пазіцый управа (r) |
A shr N |
Прыярытэт
аперацый – як у
![]() .
.
Сутнасць
аперацый
![]() і
і
![]() аднолькавая: яны зрушваюць двайковую
паслядоўнасць значэння A
на N бітаў адпаведна
ўлева або ўправа. Пры гэтым біты, якія
знікаюць за краем
разраднасці, губляюцца, а разрады,
якія вызваліліся, запаўняюцца нулямі.
Рэалізацыя аперацый
і
залежыць ад кампілятара.
аднолькавая: яны зрушваюць двайковую
паслядоўнасць значэння A
на N бітаў адпаведна
ўлева або ўправа. Пры гэтым біты, якія
знікаюць за краем
разраднасці, губляюцца, а разрады,
якія вызваліліся, запаўняюцца нулямі.
Рэалізацыя аперацый
і
залежыць ад кампілятара.
![]() паколькі
паколькі
![]() ;
;
![]() паколькі
паколькі
![]()
У даных тыпу Byte, Shortint зрушваецца поле з 8 бітаў; тыпу Word, Integer – 16 бітаў; Longint – 32 біты. Браць N больш за гэтыя велічыні або адмоўным бяссэнсава – вынікам будзе 0.
Аперацыя
можа замяняць множанне гэтых лікаў на
ступені двойкі, пры гэтым не ўзнікае
«перапаўнення», але можам
атрымаць дрэнны вынік – прападзе
старэйшы біт. Напрыклад:
![]()
![]() j shl
3 = j*8,
а shr
– цэлалікавае дзяленне на ступені
двойкі; j shl
1 = [j/2],
j shl
3 = j*8,
а shr
– цэлалікавае дзяленне на ступені
двойкі; j shl
1 = [j/2],
![]()
![]()