
- •Глава 2. Критерии надежности. Законы распределения времени до отказа
- •Критерии надежности невосстанавливаемых систем
- •1. Вероятность безотказной работы
- •2. Плотность распределения времени безотказной работы (частота отказов)
- •3. Среднее время безотказной работы (средняя наработка до отказа)
- •4. Интенсивность отказов
- •Решение. Воспользуемся формулой (14):
- •5. Гамма-процентная наработка до отказа
- •Основные показатели надежности восстанавливаемых систем
- •1.Средняя наработка на отказ и среднее время восстановления
- •2. Поток отказов. Параметр потока отказов
- •3. Функция готовности и функция простоя. Коэффициент готовности и коэффициент простоя
- •4. Коэффициент оперативной готовности
- •5. Коэффициент технического использования
- •Законы распределения, используемые при оценке надежности
- •6. Нормальное и усеченное нормальное распределение.
- •Порядок решения задач на надежность
2. Поток отказов. Параметр потока отказов
Потоком отказов называется последовательность отказов, происходящих один за другим в случайные моменты времени. Наиболее важной характеристикой потока отказов является параметр потока отказов.
Параметром потока отказов (t) называется производная (скорость изменения) среднего числа отказов объекта в момент t и определяется по формуле:
![]() (24)
(24)
где Dt - малый отрезок наработки, n(t) - число отказов, наступивших от начального момента времени до достижения наработки t.
Разность n(t+t) – n(t) представляет собой число отказов на отрезке Dt.
Наряду с параметром потока отказов в расчетах и обработке экспериментальных данных часто используют осредненный параметр потока отказов
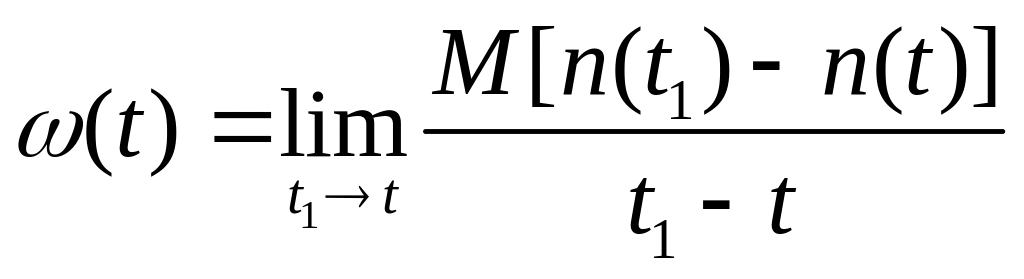 .
(25)
.
(25)
По сравнению с формулой (24) здесь рассматривается число отказов за конечный отрезок [t1, t2], причем t1£t£t2. Если поток отказов стационарный, то параметры, определяемые по формулам (24) и (25) от t не зависят.
Статистически параметр потока отказов определяется как отношение числа отказавших образцов техники в единицу времени к числу образцов, поставленных на испытание, при условии, что отказавшие образцы заменяются исправными или отремонтированными:
![]() (26)
(26)
где n(t, t+t) - количество отказавших образцов за промежуток времени [t, t+t], N0 - число образцов, поставленных первоначально на испытания.
Параметр потока отказов представляет собой плотность вероятности возникновения отказа восстанавливаемого объекта. Отказы объектов возникают в случайные моменты времени и в течение заданного периода эксплуатации наблюдается поток отказов. Существует множество математических моделей потоков отказов. Наиболее часто при решении задач надежности используют простейший поток отказов - пуассоновский поток. Простейший поток отказов удовлетворяет одновременно трем условиям: стационарности, ординарности, отсутствия последствия.
Стационарность случайного процесса (времени возникновения отказов) означает, что на любом промежутке времени ti вероятность возникновения n отказов зависит только от n и величины промежутка ti, но не зависит от сдвига ti по оси времени. Следовательно, при ti = ti+1 = ti+m вероятность появления n отказов по всем интервалам составит
![]()
Ординарность случайного процесса означает, что отказы являются событиями случайными и независимыми. Ординарность потока означает невозможность появления в один и тот же момент времени более одного отказа, т.е.
![]()
Отсутствие последствия означает, что вероятность наступления n отказов в течение промежутка ti не зависит от того, сколько было отказов и как они распределялись до этого промежутка. Следовательно, факт отказа любого элемента в системе не приведет к изменению характеристик (работоспособности) других элементов системы, если даже система и отказала из-за какого-то элемента.
Опыт эксплуатации сложных технических систем показывает, что отказы элементов происходят мгновенно и, если старение элементов отсутствует ( = const), то поток отказов в системе можно считать простейшим.
Случайные события, образующие простейший поток, распределены по закону Пуассона:
![]() при n 0
(27)
при n 0
(27)
где Рn(t) - вероятность возникновения в течение времени t ровно n событий (отказов); - параметр распределения, совпадающий с параметром потока событий.
Если в выражении (27) принять n = 0, то получим P0(t)=e--t - вероятность безотказной работы объекта за время t при интенсивности отказов = const.
Параметр потока отказов обладает следующими свойствами:
в случае экспоненциального закона времени работы объекта с параметром и мгновенного восстановления (t)= ;
при мгновенном восстановлении предел, к которому стремится параметр потока отказов при t, равен величине, обратной среднему времени безотказной работы, т. е.
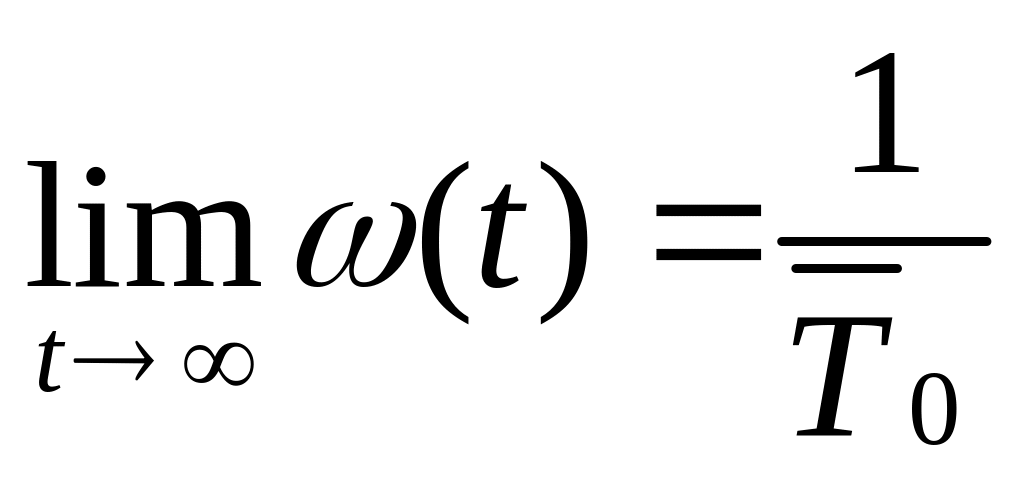 ;
;при мгновенном восстановлении параметр потока отказов и плотность распределения времени до отказа связаны следующим интегральным уравнением Вольтерра второго рода:
![]() . (27).
. (27).
Это уравнение устанавливает зависимость между показателями надежности восстанавливаемой и невосстанавливаемой техники. Оно позволяет определить по статистическим данным об отказах восстанавливаемой техники в процессе ее эксплуатации показатели надежности невосстанавливаемой техники.
Пример. Время до отказа объекта имеет нормальное распределение с математическим ожиданием Т = 1000 час и средним квадратическим отклонением = 300 час. Привести графическую иллюстрацию плотности распределения f(t) и параметра потока отказов (t) .
Решение. Графики функций изображены на рис. 4. Параметр потока отказов (t) получен путем численного решения уравнения Вольтерра.
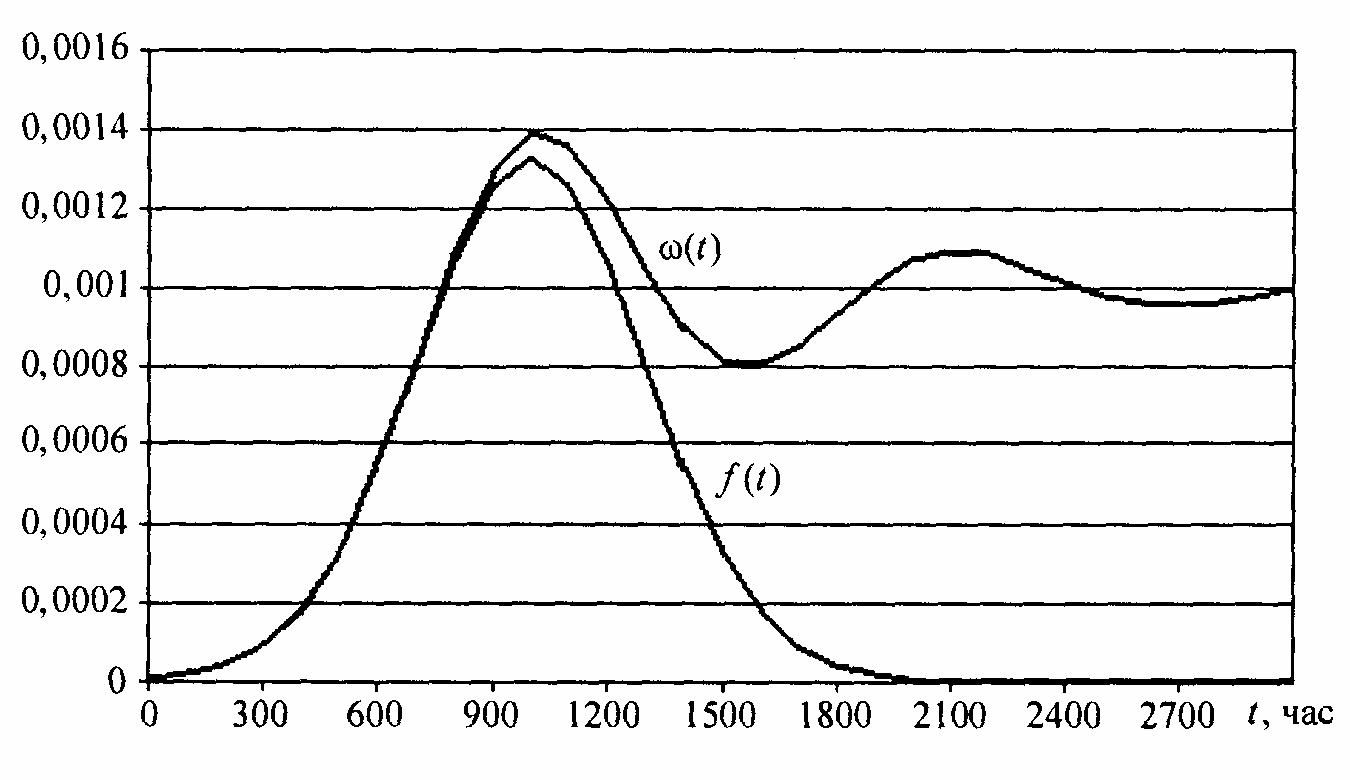
Рис.4. Графики плотности распределения f(t) и параметра потока отказов (t)
Кроме указанных (наиболее употребляемых) показателей надежности, имеются и другие показатели: средняя трудоемкость восстановления, средний срок сохраняемости, гамма-процентный ресурс, гамма-процентное время восстановления, гамма-процентный срок сохраняемости и др. При необходимости определения указанных показателей используются специальные методики, где процедура расчета основывается на тех же законах математической статистики и теории вероятностей, по которым определяются и более широко используемые показатели надежности.
Рассмотренные показатели надежности позволяют оценить надежность простых и сложных объектов. Однако они не позволяют установить соотношения между временными составляющими цикла эксплуатации. В частности, они не учитывают времени, затраченного на профилактические мероприятия и ремонт совместно с процессом функционирования объекта. Они не учитывают также удобства эксплуатации, готовности объектов к действию в данный момент времени и другие факторы. Для этого применяют различные комплексные показатели надежности.
Комплексные показатели надежности в отличие от единичных показателей характеризуют не менее двух свойств, составляющих надежность, например, безотказность и ремонтопригодность. Примерами комплексных показателей надежности служат различные коэффициенты надежности.
