ИДЗ 5 ТМиЭЭТ

Санкт-Петербургский государственный электротехнический университет

кафедра ФЭТ

Дисциплина

«Технология материалов и элементов электронной техники»

Расчет по заданию №5

Выполнил студент группы 5207

Иванов А.Д.

Преподаватель:

профессор Шаповалов В.И.

Санкт - Петербург

2018 г.

Цель работы: исследовать зависимость температуры медной пленки от плотности мощности излучения лазера в моноимпульсном режиме.

Теоретическая часть

В этой задаче образец представляет собой двухслойную структуру: пленка расположена на подложке (рис. 2.30). Оба эти элемента обычно изготовлены из разных материалов и имеют отличающиеся параметры, указание на рис. 2.30, где индекс 1 присвоен пленке, индекс 2 – подложке. Поток излучения, взаимодействуя с образцом, может частично попасть на границу раздела пленка-подложка. Часть потока поглотится пленкой, а часть отразится от ее поверхности.

Особенности нагрева пленок излучением лазера станут очевидными, если оценить толщину нагретого слоя к моменту времени t′, при котором пространственное распределение температуры в нем начинает отличаться от распределения плотности мощности в пучке. Так, для хрома t′≈2.3мс. За это время может прогреться слой пленки толщиной примерно равной 25 мкм, что значительно превышает толщину пленки. Из этого факта следует основное допущение, принятое при формулировке тепловой задачи для пленки: мощность тепловыделения в пленке постоянна в течение действия импульса и не зависит от координаты. Это означает, что допускается равномерное распределение мощности тепловыделения по толщине пленки в области диаметром 2r₀ (рис. 2.30). Для упрощения этой задачи введено еще несколько допущений: тепловой контакт пленки к подложке идеален, теплофизические параметры пленки и подложки не зависят от температуры, q0= const и r₀>> .

При указанных допущениях возникает тепловая задача, в которой разогрев пленки происходит за счет теплопроводности от объемного источника тепла. Подложка нагревается от поверхностного источника за счет потока тепла из пленки, т. е. так же, как и объемный образец. Эта задача приводит к системе из двух уравнений. Уравнение для пленки отличается тем, что в нем учитывается объемный источник тепла в виде ненулевой правой части:

Дано:

; ;

; ; ; ;

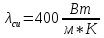Построить: Т(q₀),

Решение

1. Определим коэффициент температуропроводности

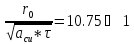– не учитываем боковой теплоотвод

2. Найдем плотность мощности

3. Определим отношение объемных теплоемкостей пленки и подложки

Данная величина близка к единице, поэтому рассмотрим и адиабатический режим, и режим теплопроводности

4. Построение зависимостей

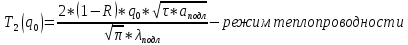
Рисунок 1 – Зависимость температуры пленки от плотности мощности

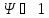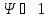Вывод: т.к. не удовлетворяет ни одному из условий или , то нельзя однозначно сказать, какого вида решение системы:

Если подложка интенсивно отбирает тепло, то одним импульсом не удастся расплавить медную пленку, в противном случае она начнет плавиться уже при плотности мощности .