Практичне заняття №1

ПРАКТИЧНЕ ЗАНЯТТЯ №1

МІНІМІЗАЦІЯ ФУНКЦІЙ АЛГЕБРИ ЛОГІКИ ЗАДАНИХ В АЛГЕБРАЇЧНІЙ ФОРМІ.

1.1. Теоретичні відомості

Важливою задачею в побудові дискретних пристроїв є спрощення виразів для ФАЛ з метою отримання такого виду формули, при якому побудований відповідно до неї автомат відрізнявся б мінімальною витратою логічних елементів на його виготовлення (в більш загальному формулюванні – мінімальною вартістю). Строге рішення цієї задачі повинне враховувати конкретні особливості логічних елементів, вживаної елементної бази, зокрема значення коефіцієнта об'єднання і розгалуження логічних елементів, число елементів в корпусах і т.д. Проте, існуючі методи спрощення формул призначенні для більш загального спрощення і не вирішують задачу в такому об'ємі.

Найбільш детально розроблені методи вирішення канонічної задачі мінімізації ФАЛ, яка полягає в знаходженні форми функції, що містить мінімальне число змінних. Такі форми називають мінімальними.

Початковими формами функції при рішенні канонічної задачі мінімізації є її ДДНФ (диз’юнктивна досконала нормальна форма) і КДНФ(кон’юнктивна досконала нормальна форма) . Якщо функція задана в іншій формі, останню перетворять в ДДНФ або КДНФ.

Для переходу від ДНФ (диз’юнктивна нормальна форма) до ДСНФ в кожного з членів, в яких представлені не всі аргументи, слід ввести вираз вигляду (де x₁ — відсутня в члені змінна).

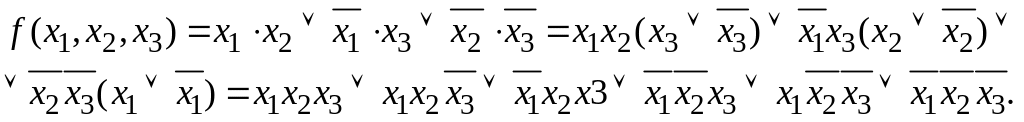(1)

Для переходу від КНФ (кон’юнктивна нормальна форма) до КСНФ до кожного члена, що не містить всіх змінних, слід додати кон'юнкції прямих і інверсних значень відсутніх змінних , після чого для отримання форми КСНФ необхідно скористатись законами АЛ:

(2)

Канонічні форми функції, ДСНФ і КСНФ є початковими при мінімізації ФАЛ. Для перетворення функцій в АЛ використовується ряд законів і тотожності, основні з яких без доказу приведені нижче.

Комутативний переміщувальний закон для диз’юнкції і кон’юнкції:

, (11)

. (12)

Дистрибутивний (розподільний) закон:

, (15)

. (16)

Закон інверсії (подвійності):

. (17)

Закон повторення (ідемпотентності):

, (18)

. (19)

Закон заперечення:

, (20)

. (21)

Закон подвійного заперечення:

. (22)

Закон поглинання:

, (23)

. (24)

Правила для операцій з константами:

, (25)

, (26)

, (27)

, (28)

, (29)

. (30)

Закон склеювання:

. (31)

Додаткова тотожність:

, (32)

. (33)

Практичне використання закону поглинання в кон’юнктивній формі. Для схеми на безконтактних елементах, в якій на виході знаходиться елемент «І» на вхід якого поступає змінна х на входах всіх елементів схеми замість однойменних значень змінної можна поставити 1, а замість різнойменних 0. Якщо схема представлена в контактній реалізації, і послідовно із загальною схемою включений одиночний контакт реле х, всі однойменні по дії контакти цього реле, задіяні в схемі, можна закоротити, а всі різнойменні по дії контакти – виключити (рис .1.1).

Рис. 1.1. Схеми, що перетворюються на основі закону поглинання в кон’юнктивній формі і отримані в результаті перетворення: а) – на логічних елементах; б) – на контактах реле.

Практичне використання закону поглинання в диз'юнктивній формі. Для схеми на безконтактних елементах включений елемент «АБО», на вхід якого поступає змінна х, на входах всіх елементів схеми замість однойменних значень змінної можна поставити 0, а замість різнойменних 1. Якщо схема представлена в контактній реалізації, і на схемі паралельно із загальною схемою включений одиночний контакт реле х, всі однойменні по дії контакти цього реле, задіяні в схемі, можна виключити, а всі різнойменні по дії контакти – закоротити (рис. 1.2).

Рис. 1.2. Схеми, що перетворюються на основі закону поглинання в диз’юнктивній формі і отримані в результаті перетворення: а) – на логічних елементах; б) – на контактах реле.

1.2. Порядок виконання роботи

1.2.1. Вивчити за даними методичними вказівками і літературою, що рекомендується, основні положення алгебри логіки;

1.2.2. Представити ФАЛ, вибрану з табл. 1.1 відповідно до варіанту, в диз'юнктивній і кон’юнктивній досконалих нормальних формах;

1.2.3. Використовуючи основні закони та тотожності АЛ, виконати мінімізацію ФАЛ, що розглядається як у диз’юнктивній так і у кон’юнктивній формах (в ідеальному випадку результати мінімізації повинні співпадати).

1.3. Зміст звіту

Звіт повинен містити:

• Найменування роботи;

• Доповнені висновками і коментарями результати виконаних завдань, передбачених пунктами 1.2.2, 1.2.3;

Таблиця 1.1

Варіанты ФАЛ

a	b	c	d	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	1	1	1	1	1	1	1	0	0	0	1	1	1	1	1
0	0	0	1	1	0	1	1	1	0	1	0	1	1	1	0	0	1	0
0	0	1	0	0	1	1	0	0	1	0	1	1	1	1	0	1	1	0
0	0	1	1	0	0	1	0	1	1	1	1	0	0	0	1	1	0	1
0	1	0	0	1	1	0	1	1	1	1	0	1	0	0	1	1	1	1
0	1	0	1	0	1	1	0	0	0	1	1	1	0	0	1	1	0	1
0	1	1	0	1	1	1	1	1	0	1	1	1	1	0	1	1	1	1
0	1	1	1	0	0	1	1	1	1	1	1	0	1	0	1	1	0	0
1	0	0	0	1	0	1	0	1	1	1	0	1	0	0	0	0	0	0
1	0	0	1	1	0	1	1	0	0	0	0	1	0	0	0	1	1	1
1	0	1	0	0	1	1	0	0	0	1	1	0	0	0	1	1	1	0
1	0	1	1	0	1	1	0	1	0	1	0	1	1	1	0	1	0	0
1	1	0	0	0	0	0	0	1	0	1	1	1	0	1	1	0	1	0
1	1	0	1	1	0	1	1	1	0	1	0	0	1	1	1	1	1	0
1	1	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
1	1	1	1	1	0	0	0	0	0	0	0	0	1	0	0	1	0	0

ЛІТЕРАТУРА

1. Сапожников В.В. и др. Теория дискретных устройств железнодорожной автоматики и телемеханики. М.: 2001.

2. Сапожников В.В. и др. Дискретные устройства железнодорожной автоматики, телемеханики и связи. -М.: Транспорт, 1988.-256с.

3. Голсуорт В.В. Проектирование цифровых логических устройств.-М.:Машиностроение, 1985.- 226 с.

4. Дискретные устройства автоматизированных систем управления /Под ред. Г.Н.Тимонькина.-Харьков, 1990.-511 с.

5. Методичні вказівки до виконання лабораторних робіт.