- •Оглавление
- •Основные понятия.
- •Процесс оптимизации.
- •2 Вида задач оптимизации:
- •Методы одномерной оптимизации.
- •2 Варианта:
- •2 Способа:
- •Аналитический способ нахождения локального минимума.
- •Численные методы.
- •Методы одномерного поиска.
- •Метод золотого сечения.
- •Одномерная оптимизация с использованием производных.
- •Методы для нахождения корня уравнения функции 1-ой переменной.
- •Метод Ньютона (метод касательной):
- •Обобщение
- •Безусловная оптимизация.
- •Функции 2-х переменных
- •Квадратичная аппроксимация (или квадратичное приращение)
- •Методы прямого поиска.
- •Метод координатного спуска.
- •Градиентные методы. Метод наискорейшего спуска.
- •Анализ метода.
- •Метод Ньютона.
- •1 И 2 не подходят для оптимизации.
- •Недостатки:
- •Задачи оптимизации с ограничениями – разностями (зор)
- •Метод исключения
- •Метод множителей Лагранжа.
- •5 Условий дают систему линейных уравнений Нелинейное программирование (нлп).
- •Задачи линейного программирования (лп).
Одномерная оптимизация с использованием производных.
![]() .
Пусть целевая функция дифференцируема
.
Пусть целевая функция дифференцируема
![]() .
.
|
|
|
точка локального минимума |
точка локального максимума |
точка перегиба |
Методы для нахождения корня уравнения функции 1-ой переменной.
Деление пополам:
Имеется хотя бы 1 корень. Выбираем любую точку и смотрим какой знак она имеет, такой знак нам и искать. Выбираем точку приблизительно в середине интервала, исследуя значения в 3-х можно отбросить половину интервала.


 +
+



 b
b
а
-
Метод Ньютона (метод касательной):
В случае если известна производная, то
выбираем
![]() -
начальное приближение.
-
начальное приближение.




![]()

![]()
![]()
![]()
Допустим, что
точка
достаточно близка к корню функции и
примерно себя ведет линейно не отклоняется.
Проведем касательную и находим точку
ближе чем
,
и повторяем до
![]() .
.
Для метода Ньютона необходимо:
функция должна иметь производную;
точка должна быть взята близко к корню;
функция изменяется близко к линейной функции.
![]() ;
;
![]() - уравнение касательной;
- уравнение касательной;
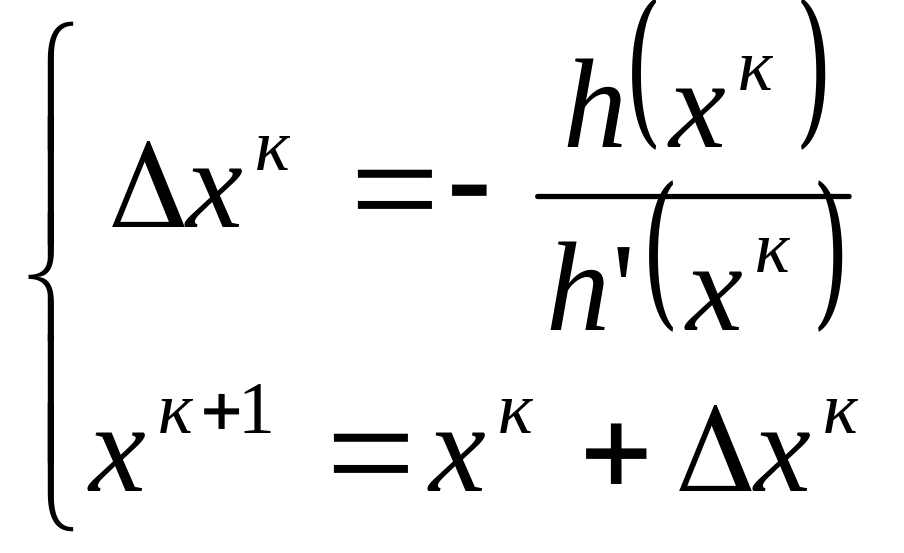 .
.
Если
![]() ,
то вычисления можно прекратить и считать
что нужный нам корень – условие
прекращения поиска. (Е – значение корня
с некоторой точностью).
,
то вычисления можно прекратить и считать
что нужный нам корень – условие
прекращения поиска. (Е – значение корня
с некоторой точностью).
В методе Ньютона каждя его итерация удваивает количество значащих цифр. Если все условия выполнены, то эти методы удваивают (ускоряют) количество значащих цифр:
![]() ;
;
Представим что
![]() линейная функция, то метод Ньютона
позволяет найти ее корень за 1-у
итерацию. Целевая функция представляет
собой квадратичную зависимость
следовательно метод Ньютона позволяет
найти минимум или максимум квадратичной
функции за 1-у итерацию.
линейная функция, то метод Ньютона
позволяет найти ее корень за 1-у
итерацию. Целевая функция представляет
собой квадратичную зависимость
следовательно метод Ньютона позволяет
найти минимум или максимум квадратичной
функции за 1-у итерацию.
Замена функции на касательную, называется – линейная аппроксимация, и ее применение к целевой функции парабола в точке приближения.

f(x)


![]() х
х
Замена заданной зависимости квадратичной зависимостью, называется – квадратичной аппроксимацией. Метод Ньютона основан на замене заданной зависимости более простой зависимостью.
Обобщение
На практике часто необходимо найти
экстремум (или экстремумы) некоторой
целевой функции
![]() переменных
переменных
![]() (проектных параметров). Такая функция
описывает
(проектных параметров). Такая функция
описывает
![]() -
мерную поверхность. Соответственно
функция
-
мерную поверхность. Соответственно
функция
![]() одного параметра
одного параметра
![]() описывает некоторую кривую на плоскости.
Поиск экстремумов функции одной
переменной является самостоятельной
и часто встречающейся задачей.
описывает некоторую кривую на плоскости.
Поиск экстремумов функции одной
переменной является самостоятельной
и часто встречающейся задачей.
Метод равномерного поиска
основан на том, что переменной
присваиваются значения
![]() с шагом
с шагом
![]() и вычисляются значения
.
Если
и вычисляются значения
.
Если
![]() переменной
даётся новое приращение. Как только
переменной
даётся новое приращение. Как только
![]() станет меньше
станет меньше
![]() ,
поиск останавливается. При малой заданной
погрешности этот метод неэкономичен
по затратам машинного времени.
,
поиск останавливается. При малой заданной
погрешности этот метод неэкономичен
по затратам машинного времени.
Метод поразрядного приближения является разновидностью метода равномерного поиска и реализуется следующим алгоритмом.
Задаём начальное приближение
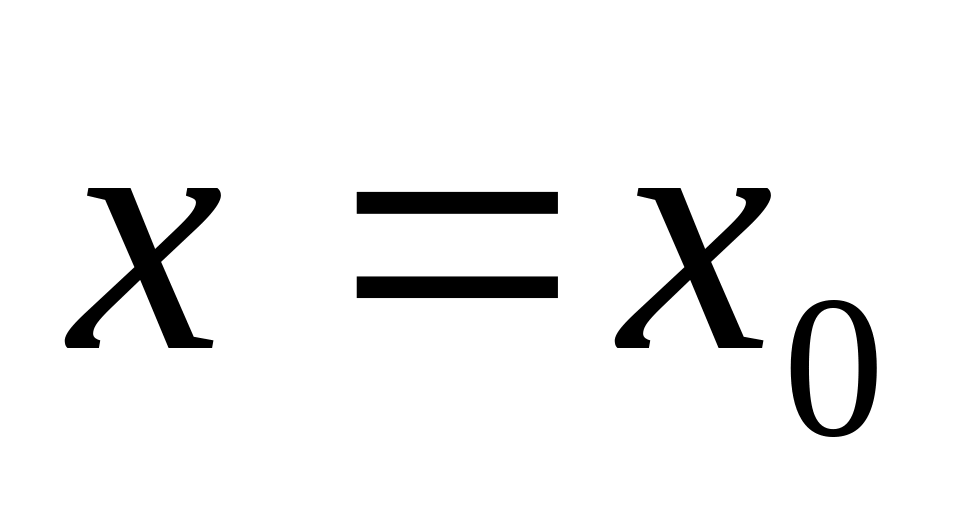 слева от максимума
слева от максимума
 и вычисляем
и вычисляем
 .
Задаём
.
Задаём
 где
где
 -
начальный шаг поиска.
-
начальный шаг поиска.Полагаем
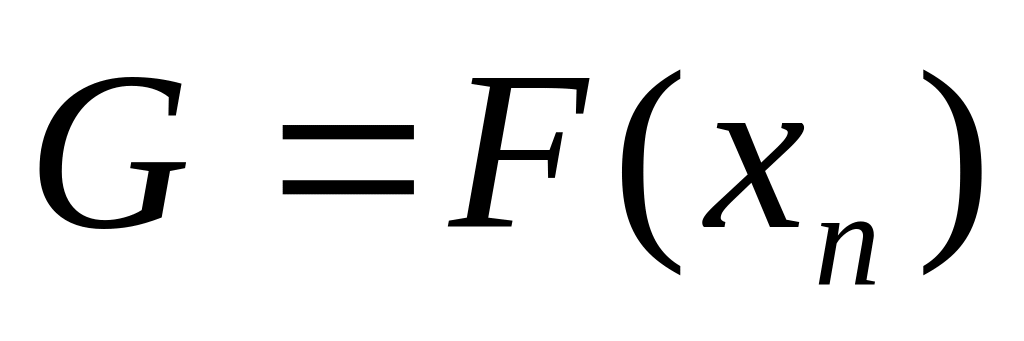 ,
где вначале
,
где вначале
 задаём
задаём
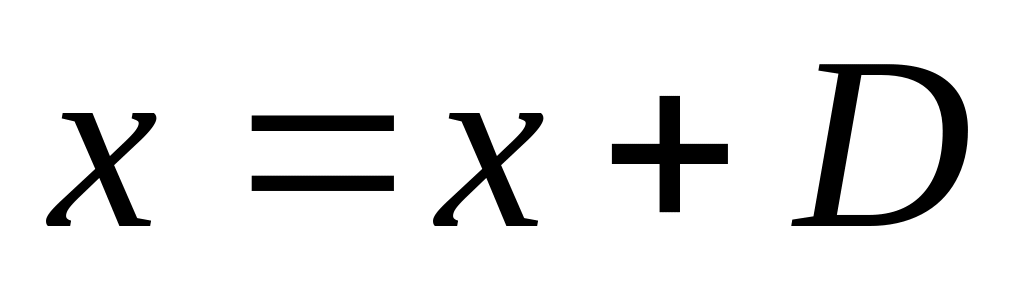 и вычисляем
и вычисляем
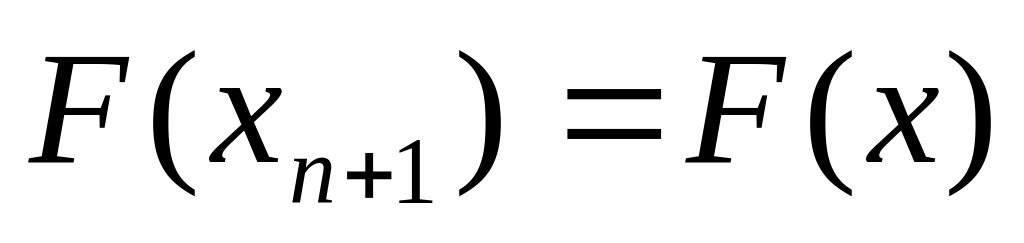 .
.Проверяем условие
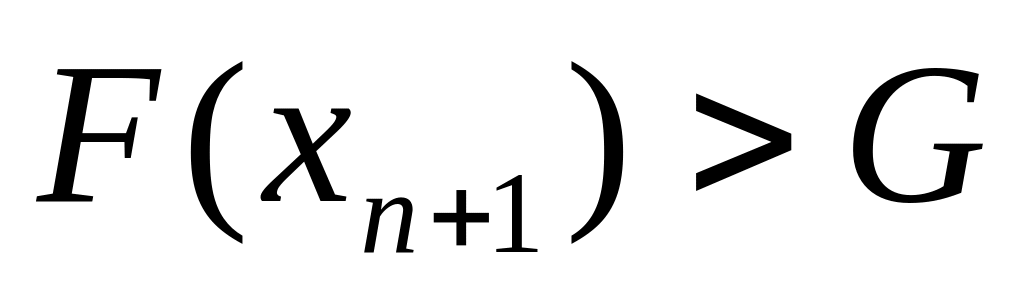 ;
если оно выполняется, идём к п. 3, если
нет – к п. 4.
;
если оно выполняется, идём к п. 3, если
нет – к п. 4.Полагаем
 .
Проверяем условие
.
Проверяем условие
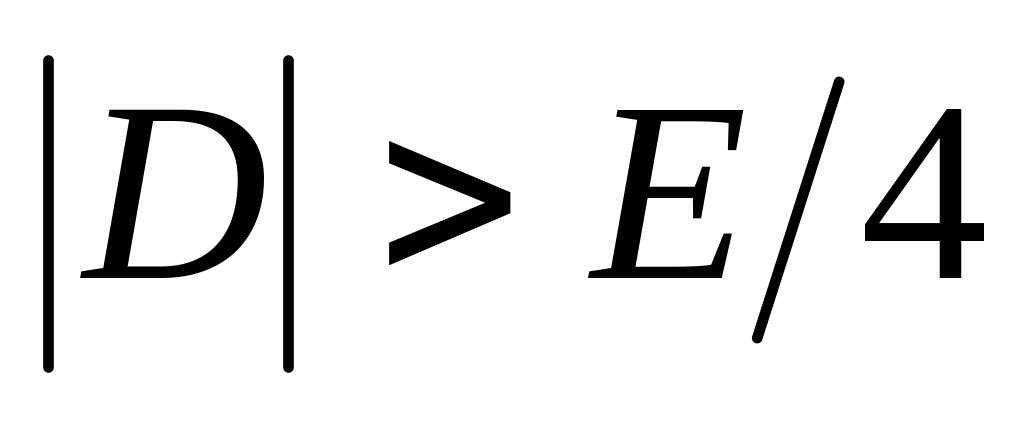 ,
где
,
где
 - заданная погрешность вычисления
- заданная погрешность вычисления
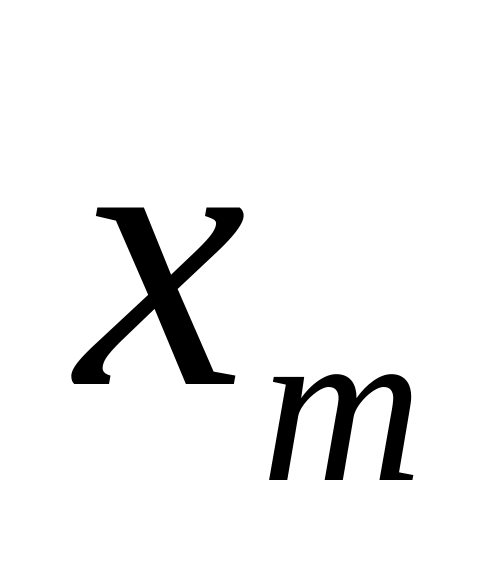 в точке максимума. Если оно выполняется,
идём к п. 2, т. е. обеспечиваем поиск
максимума в другом направлении с шагом
в 4 раза меньше прежнего. Если данное
условие выполнятся, заканчиваем поиск.
в точке максимума. Если оно выполняется,
идём к п. 2, т. е. обеспечиваем поиск
максимума в другом направлении с шагом
в 4 раза меньше прежнего. Если данное
условие выполнятся, заканчиваем поиск.
Метод дихотомии (деления интервала
поиска
![]() пополам) реализуется следующим образом.
пополам) реализуется следующим образом.
Проверяем условие
 ,
где
- заданная погрешность вычисления
.
Если это условие выполняется, идём к
п. 6; если не выполняется, идём к п. 2.
,
где
- заданная погрешность вычисления
.
Если это условие выполняется, идём к
п. 6; если не выполняется, идём к п. 2.Делим интервал поиска пополам и вычисляем две абсциссы, симметрично расположенные относительно точки
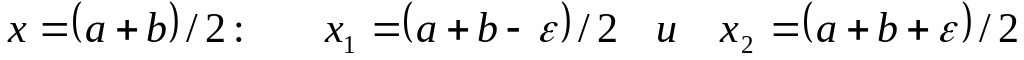 .
.Для этих значений вычисляем
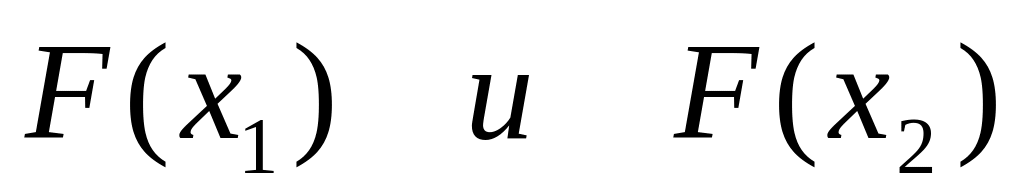 .
.Проверяем условие
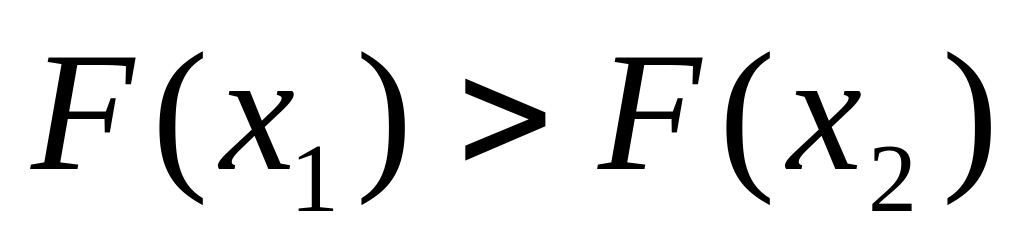 .
Если оно выполняется, полагаем
.
Если оно выполняется, полагаем
 и идём к п. 1. Если не выполняется, идём
к п. 5.
и идём к п. 1. Если не выполняется, идём
к п. 5.Полагаем
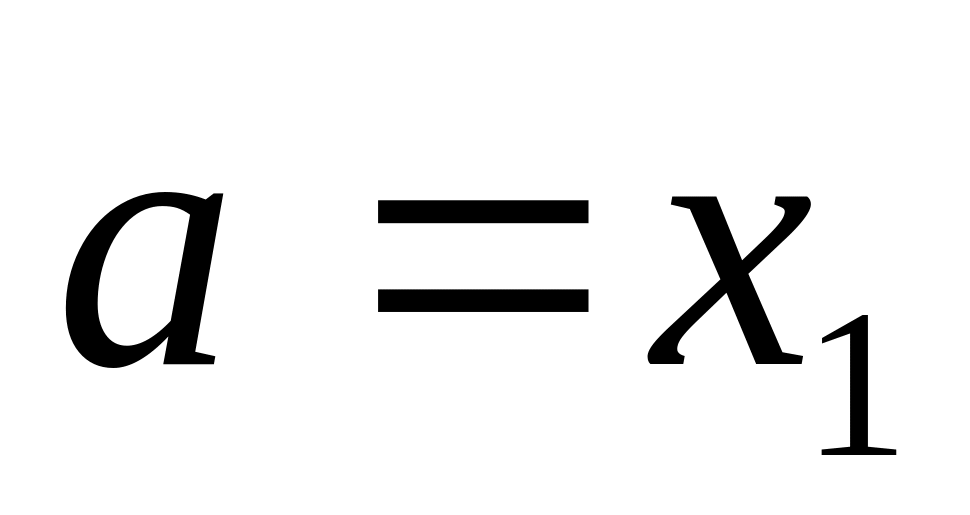 и идём к п. 1.
и идём к п. 1.Выводим на печать
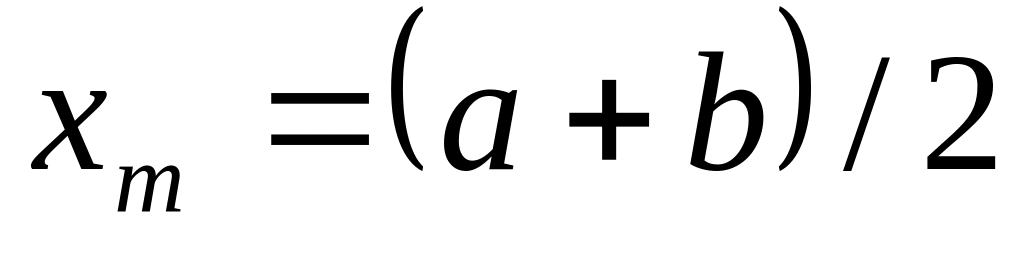 и вычисляем
и вычисляем
 .
.
Метод золотого сечения основан на делении отрезка по правилу золотого сечения. Он позволяет сужать отрезок , каждый раз вычисляя лишь одно значение , а не два, как в методе дихотомии. Данный метод реализуется следующим алгоритмом.
Находим коэффициент дробления
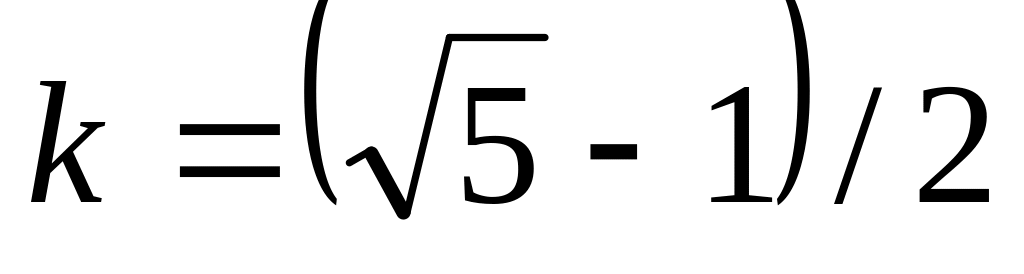 отрезка
.
отрезка
.Находим абсциссу
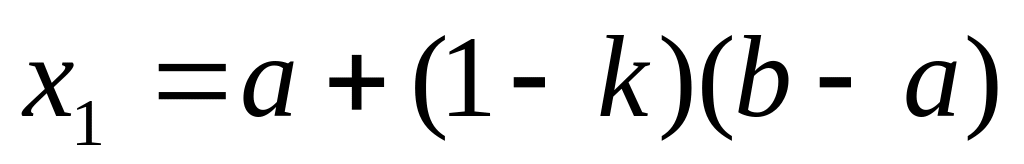 и вычисляем
и вычисляем
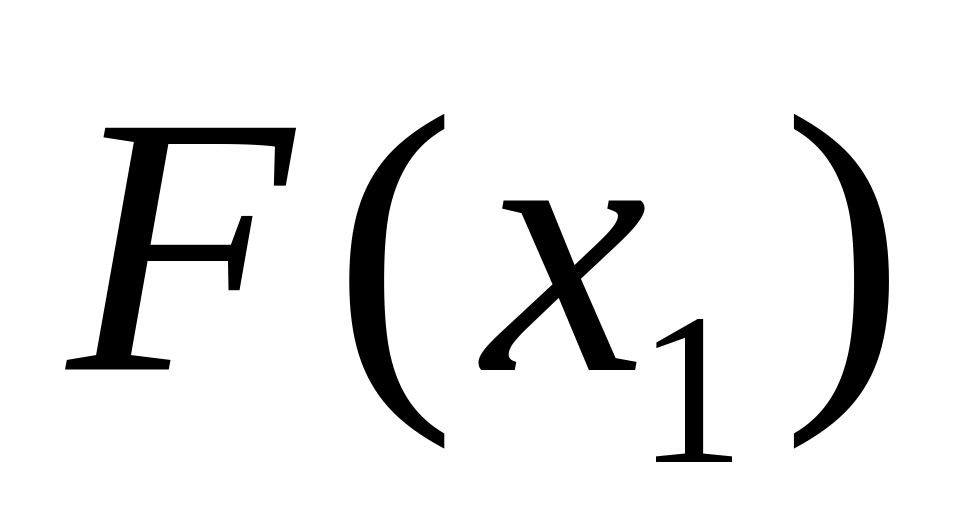 .
.Находим абсциссу
 и вычисляем
и вычисляем
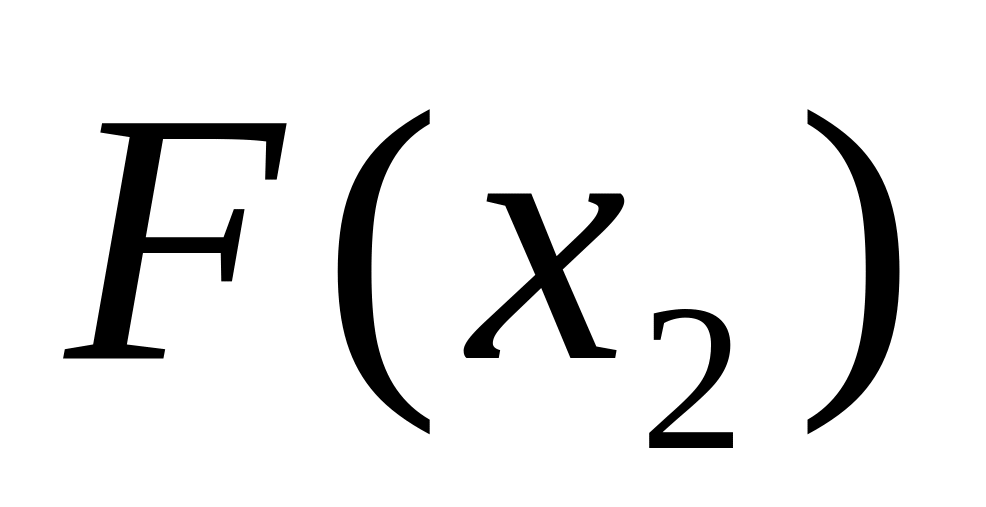 .
.Проверяем выполнение условия
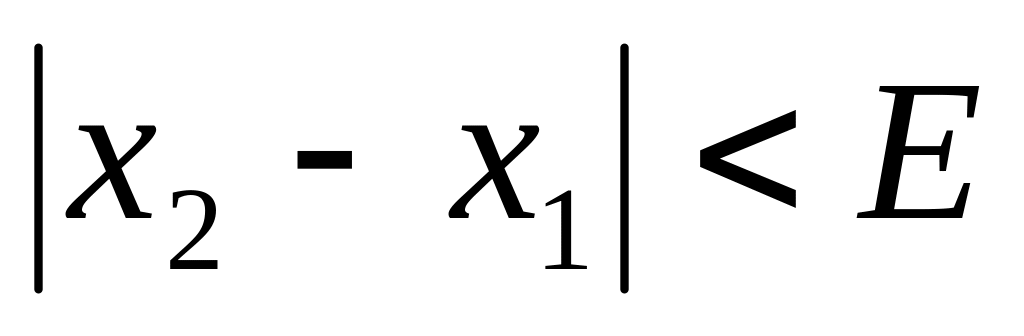 ,
где
- заданная погрешность вычисления
.
Если это условие выполняется, вычисляем
,
где
- заданная погрешность вычисления
.
Если это условие выполняется, вычисляем
 и
,
после чего останавливаем счёт с выдачей
значений
и
.
Если данное условие не выполняется,
идём к п. 5.
и
,
после чего останавливаем счёт с выдачей
значений
и
.
Если данное условие не выполняется,
идём к п. 5.Проверяем условие
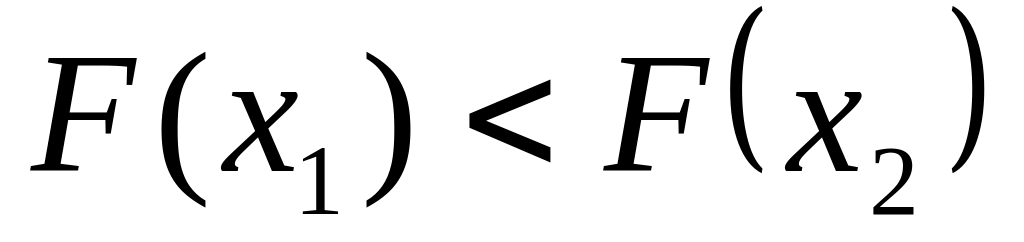 .
Если оно выполняется, полагаем
.
Если оно выполняется, полагаем
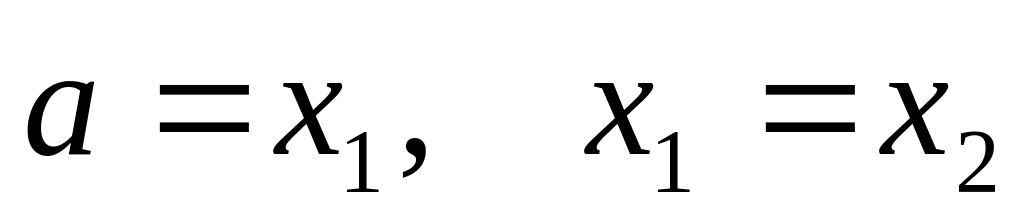 и
и
 ,
после чего выполняем п.3 и п. 4.
,
после чего выполняем п.3 и п. 4.Если
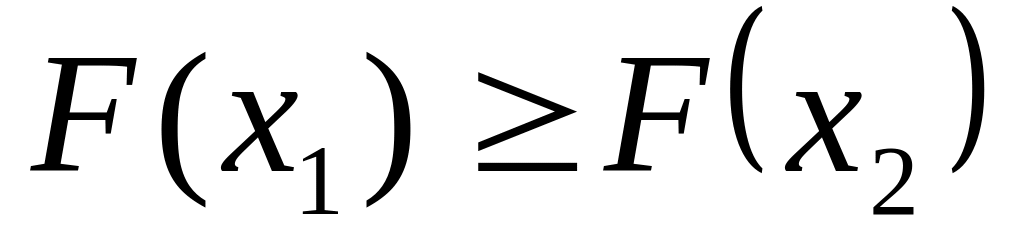 ,
полагаем
,
полагаем
 ,
, ,
после чего выполняем п. 2.
,
после чего выполняем п. 2.