32 Оптимальные задачи зи. Постановка задачи. Классификация методов принятия решения в зи

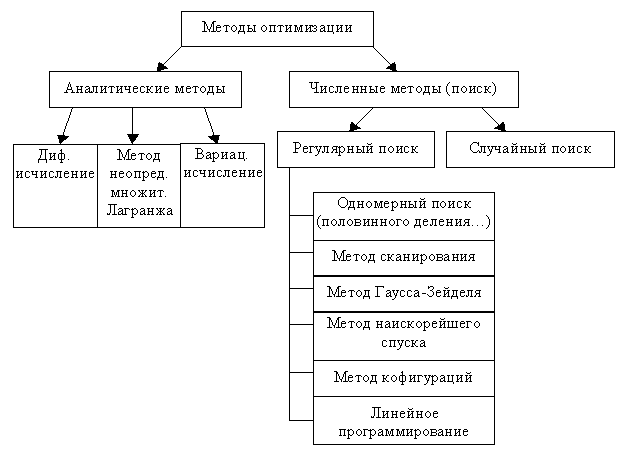
Аналитические методы — решение в явном виде.

Численные методы (поиск) — решение с помощью некоторого алгоритма.

Регулярный поиск — строго определённый порядок действий.

Случайный поиск — порядок поиска может меняться.

Аналитические методы :

Дифференциальное исчисление: 1)

2) (i = 1, 2, …,n)

3) Унимодальность.

Метод неопределённых множителей Лагранжа:

F(X)  max при _I(X)=0;

Функция Лагранжа: F₀=F+  max; ,

Регулярный поиск:

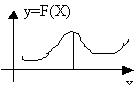
Одномерный поиск: Для унимодальных функций.

Метод Гаусса-Зейделя: метод покоординатного спуска.

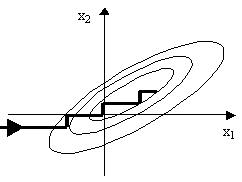
Метод наискорейшего спуска: F  max, ,…, , x= x^+hgradF(x^).

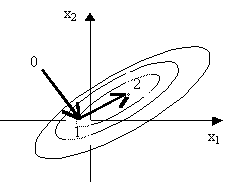
Метод конфигураций: может использоваться для движения по гребню.

x₂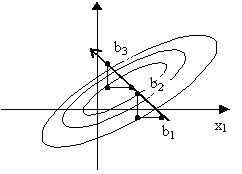

Линейное программирование:

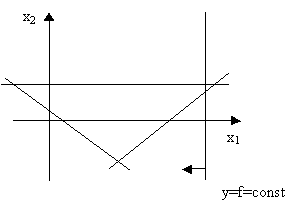
Случайный поиск: x_j=x_i^+_i , где _i  (-1; 1).

Лёгкий случайный поиск с возвратом.

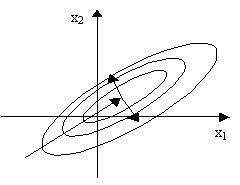
Особенности практического применения методов оптимизации.

Сложности задач оптимизации:

Высокая размерность (1020)

Оценка значимости параметров

Нормализация:

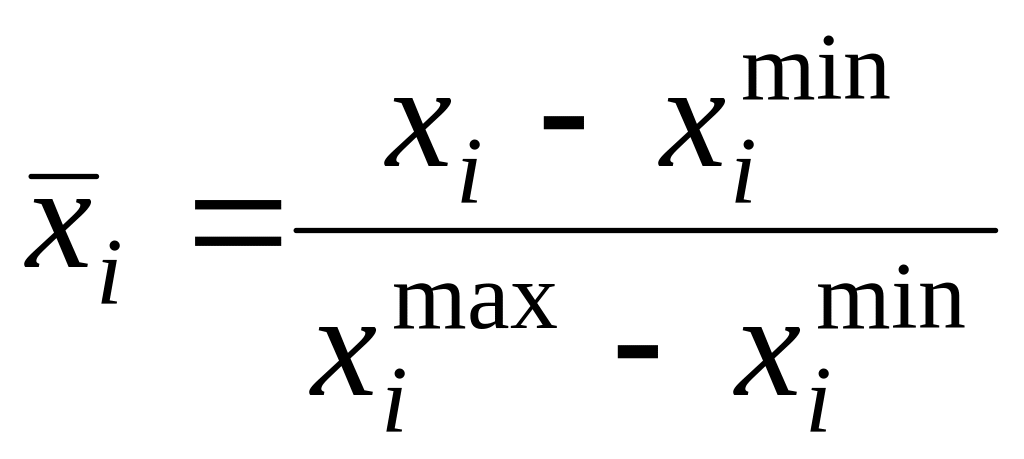, здесь (0 1).

Наличие ограничений.

– Область X  G — может быть и пустой (), т.е. ограничение — «жёстко».

– Метод штрафных функций: y=F(x)+ (x), функция штрафа для ограничения (x)0;  (x)=max0, (x)²r;

Многоэкстремальность, наличие глобального экстремума.

Метод сканирования; многоэтапные процедуры.

Овраги (гребни) функции цели.

Применение алгоритмов оптимизации в экстрем. и самонастр-ся САУ:

а) Блок-схема СНС:

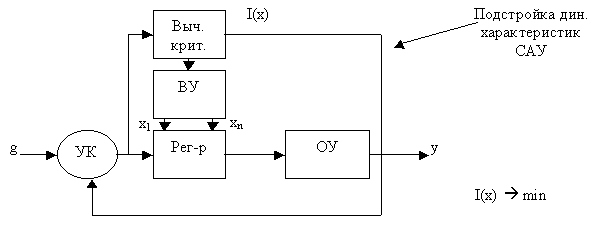
б) Блок-схема экстр. САУ:

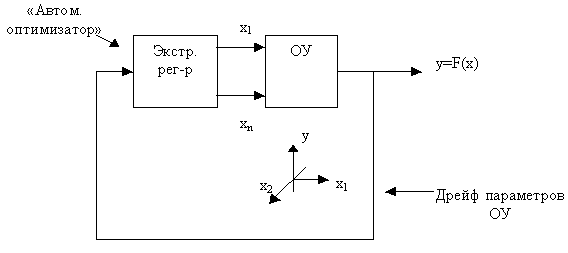
Доп. Литература:

Дуглас Дж. Уайлд «Методы поиска экстремума», -М.: Наука, 1967, 268 с.

Первозванский А.А. «Поиск», -М.: Наука, 1970, 264 с.

Пример задач имитационного моделирования.

Изучение экологических проблем (Никита Николаевич Моисеев, дир-р ВЦ АН СССР, г Алма-Ата, 1986 г.).(«экология» — «изучение собственного дома»)

Работы по изучению биосферы были включены в план ВЦ АН СССР в 1971 г.

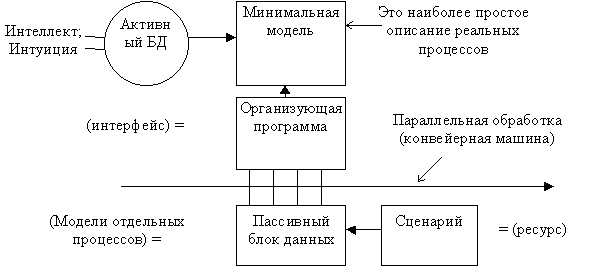
Первая версия модели биосферы 12-15 лет на её разработку.

Подробнее см. [Человек и биосфера, Александров, Моисеев], 1984 г.

Тестирование моделей — только на ЭВМ =(«звериное лицо объективной истины»).

Машинные эксперименты:

Влияние содержания углекислоты на состояние окружающей среды;

Анализ влияния пожаров (облака сажи) на земной климат.

Сценарий: Взаимный обмен ядерными ударами мощ. 5000 мГтонн.

СССР — проверяли  на 360 дней (упрощ. модель).

США — проверяли  на 30 дней (полная модель с учётом океана).

Результаты совпали.

Взрыв мощностью 1 мГт  300400 тыс.т пыли

10000 мГт  34 млрд.т пыли.

13% ядерного потенциала  превращается в костёр 1 млн.кв.км леса 

 около 4 млрд.т. сажи.

Облака сажи над городами  в 100 раз плотнее облаков, обр-ся в рез-те лесных пожаров.  «Ядерная ночь» + «Ядерная зима» (в Сев.Европе температура падает  на 30 С, на восточном побережье США  на 40-50 С).

100 мГтонн = общая взрывная мощь зарядов одной-двух подв. лодок типа

«Трайдент –2».

Зондирование пространства параметров [Соболь И.М., _{Статников} Р.Б. Наилучшие решения — где их искать. –М: Знание, 1982, 64 с.]

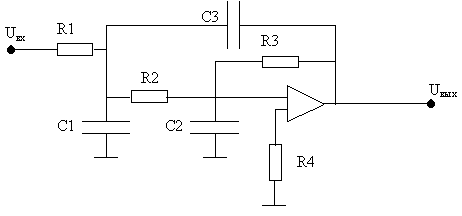
Задача: требуется найти значения параметров R1, R2, R3, R4, C1, C2, C3, при которых АЧХ фильтра максимально близка к заданной (идеальной) характеристике:

Критерий качества:

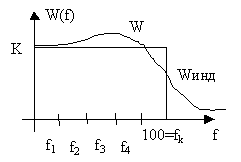
Параметры ФНЧ при этом будут удовлетворять следующим ограничениям:

Ri^H  R_i  R_i^B

C_i^H C_i  C_i^B

Зондирование — численное исследование пространства параметров X=(x₁, x₂, …,x_n) с целью определить наилучшие сочетания этих параметров.

Пример зондирования: интервал изменения каждой переменной x_i делится на m частей, итого получается mⁿ точек в узлах сетки. Всего 4²=16 точек, но если F(x₁,x₂) зависит только от x₁, то 12 точек являются «лишними», неинформативными.

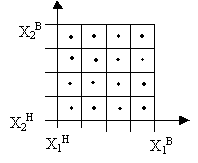
Более рациональная схема маш. эксп-та — Проекции точек на любую грань прямоугольника (в общем случае параллелепипеда) также образуют хорошие сетки. Желательно чтобы соответствующие точки имели закон распределения, близкий к равномерному; т.е. закон распределения точек должен быть случайным.

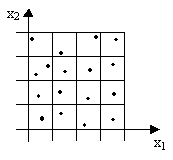
Этапы решения поставленной задачи:

Выбор пробных точек A_i (I=1, 2, …, N);

Составление таблиц испытаний:

Здесь A_i  {x₁, x₂, …, x_n} — пробные точки в заданной части пространства.

Fj Ai	F1	F2
A1 A2 A3 An	F1(A1) F1(A2) F1(A3) F1(An)	F2(A1) F2(A2) F2(A3) F2(An)

(A_1, A_2, …, A_n) — равномерно распределённые точки.

Определяются границы изменения критериев: min F₁  F₁  max F₁;

Min F₂  F₂  max F₂.

Выбор критериальных ограничений: на этой стадии — ЛПР — может назначать дополнительные критериальные ограничения: F₁  F₁^* и F₂  F₂^*, тем самым исключая из таблицы испытаний некоторые строки, т.е. некоторые испытательные точки A_i.

Исключение неэффективных точек:

Выберем какую либо из имеющихся допустимых точек, например A₁. Просматривая все другие точки A_i, кроме отмеченной, исключим те из них, для которых выполняются условия:

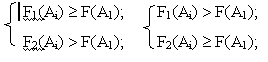
– При этом из рассмотрения исключаются все безусловно худшие точки, чем A₁. Затем среди оставшихся точек выберем какую-либо другую, отметим её и повторим процесс исключения.

– В итоге получим множество приближенно эффективных точек (при N   получаем в пределе множество эффективных точек).

5) а) Можно построить приближенную границу Парето-области.

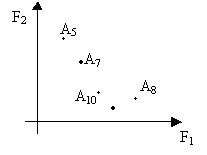
б) Можно найти корреляционную зависимость критериев F₁ и F₂ :

, где ,

r_kl — коэффициент корреляции.

Если r_kl 1, то F_k и F_l — лин. зависимость.