
- •080105.65 ‑ Финансы и кредит;
- •080107.65 – Налоги и налогообложение;
- •080103.65 ‑ Национальная экономика
- •Введение 5
- •Введение
- •Глава 1. Корреляционный анализ §1.1. Корреляционный анализ в сильных шкалах
- •§1.2. Корреляционный анализ в слабых шкалах
- •Глава 2. Парный регрессионный анализ §2.1. Линейная модель парной регрессии
- •§2.2. Парный линейный регрессионный анализ в ms Excel
- •2.2.1. Добавление линейного тренда
- •2.2.2. Интерпретация линии тренда
- •2.2.3. Усовершенствование линии тренда
- •2.2.4. Инструмент анализа Регрессия
- •2.2.5. Интерпретация регрессии
- •2.2.6. Диаграммы регрессии
- •2.2.6. Регрессионные функции
- •§2.3. Парный нелинейный регрессионный анализ в ms Excel
- •2.3.1. Полиномиальное приближение
- •2.3.2. Логарифмическое приближение
- •2.3.3. Показательное приближение
- •2.3.4. Экспоненциальное приближение
- •Глава 3. Множественный линейный регрессионный анализ
- •§3.1. Спецификация модели. Отбор факторов при построении уравнения множественной регрессии
- •§3.2. Метод наименьших квадратов (мнк). Свойства оценок на основе мнк
- •§3.3. Проверка существенности факторов и показатели качества регрессии
- •§3.4. Линейные регрессионные модели с гетероскедастичными остатками
- •§3.5. Обобщенный метод наименьших квадратов (омнк)
- •§3.6. Регрессионные модели с переменной структурой (фиктивные переменные)
- •Решение
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Глава 4. Множественный линейный регрессионный анализ средствами ms Excel
- •§4.1. Интерпретация результатов регрессии
- •Значимость коэффициентов
- •Интерпретация регрессионных статистик
- •Интерпретация анализа дисперсии
- •§4.2. Анализ остатков
- •§4.3. Использование линии тренда для прогноза
- •Интерпретация прогноза
- •Глава 5. Гетероскедастичность и автокорреляция
- •§5.1. Обнаружение гетероскедастичности
- •Графический анализ остатков
- •Тест ранговой корреляции Спирмена
- •Тест Голдфелда-Квандта
- •§5.2. Методы смягчения проблемы гетероскедастичности
- •Дисперсии отклонений известны (метод взвешенных наименьших квадратов)
- •5.2.2. Дисперсии отклонений неизвестны
- •§5.3. Автокорреляция
- •Суть и причины автокорреляции
- •Обнаружение автокорреляции
- •Математико-статистические таблицы в.1. Таблица значений -критерия Фишера при уровне значимости
- •В.2. Критические значения -критерия Стьюдента при уровне значимости 0,10, 0,05, 0,01 (двухсторонний)
- •В.3. Значения статистик Дарбина-Уотсона при 5%-ом уровне значимости
- •Список основной литературы
- •Александр Леонидович осипов Евгений Алексеевич рапоцевич практикум по эконометрике
- •080105.65 ‑ Финансы и кредит;
- •080107.65 – Налоги и налогообложение;
- •080103.65 ‑ Национальная экономика
Тест Голдфелда-Квандта
В данном случае предполагается,
что стандартное отклонение
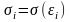 пропорционально значению
переменной
в этом наблюдении, то есть
пропорционально значению
переменной
в этом наблюдении, то есть
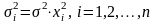 .
.
Тест Голдфелда-Квандта состоит в следующем:
Все наблюдений упорядочиваются по величине .
Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей
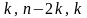 соответственно.
соответственно.Оцениваются отдельные регрессии для первой подвыборки (
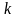 первых наблюдений) и для третьей
подвыборки (
последних наблюдений). Для парной
регрессии Голдфелд и Квандт предлагают
следующие пропорции:
первых наблюдений) и для третьей
подвыборки (
последних наблюдений). Для парной
регрессии Голдфелд и Квандт предлагают
следующие пропорции:
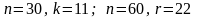 .
Если предположение о пропорциональности
дисперсий отклонений значениям
верно, то дисперсия регрессии по первой
подвыборке (рассчитываемая как
.
Если предположение о пропорциональности
дисперсий отклонений значениям
верно, то дисперсия регрессии по первой
подвыборке (рассчитываемая как
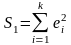 )
будет существенно меньше дисперсии
регрессии по третьей подвыборке
(рассчитываемой как
)
будет существенно меньше дисперсии
регрессии по третьей подвыборке
(рассчитываемой как
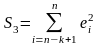 ).
).
Для сравнения соответствующих дисперсий строится соответствующая -статистика:
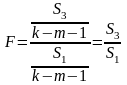 .
Здесь
.
Здесь
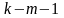 - число степеней свободы соответствующих
выборочных дисперсий (
- количество объясняющих переменных в
уравнении регрессии). Построенная
-статистика
имеет распределение Фишера с числом
степеней свободы
- число степеней свободы соответствующих
выборочных дисперсий (
- количество объясняющих переменных в
уравнении регрессии). Построенная
-статистика
имеет распределение Фишера с числом
степеней свободы
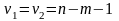 .
.Если
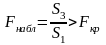 (где
(где
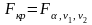 ,
определяется по таблице,
- выбранный уровень значимости), то
гипотеза об отсутствии гетероскедастичности
отклоняется.
,
определяется по таблице,
- выбранный уровень значимости), то
гипотеза об отсутствии гетероскедастичности
отклоняется.
Критическое значение - статистики рассчитывается с помощью функции MS Excel FРАСПОБР, в панели которой вводятся значения пороговой значимости (например, 0,05) и степени свободы .
Этот же тест может использоваться
при предположении об обратной
пропорциональности между
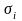 и значениями объясняющей переменной.
При этом статистика Фишера имеет вид:
и значениями объясняющей переменной.
При этом статистика Фишера имеет вид:
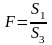 .
Для множественной регрессии данный
тест обычно применяется для той
объясняющей переменной, которая в
наибольшей степени связана с
.
При этом
должно быть больше, чем
.
Для множественной регрессии данный
тест обычно применяется для той
объясняющей переменной, которая в
наибольшей степени связана с
.
При этом
должно быть больше, чем
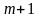 .
Если нет уверенности относительно
выбора переменной
,
то данный тест может осуществляться
для каждой из объясняющих переменных.
.
Если нет уверенности относительно
выбора переменной
,
то данный тест может осуществляться
для каждой из объясняющих переменных.
§5.2. Методы смягчения проблемы гетероскедастичности
Как отмечалось ранее,
гетероскедастичность приводит к
неэффективности оценок, что может
привести к необоснованным выводам по
качеству модели. Поэтому при установлении
гетероскедастичности необходимо
преобразовать модель с целью устранения
данного недостатка. Вид преобразования
зависит от того, известны или нет
дисперсии
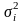 отклонений
отклонений
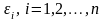 .
.
Дисперсии отклонений известны (метод взвешенных наименьших квадратов)
Данный метод применяется при известных для каждого наблюдений значений . В этом случае можно устранить гетероскедастичность, разделив каждое наблюдаемое значение на соответствующее ему значение дисперсии. В этом суть метода взвешенных наименьших квадратов (ВМНК).
Для простоты рассмотрим
взвешенный метод наименьших квадратов
на примере парной регрессии
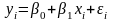 .
Разделим обе части
на известное
.
Разделим обе части
на известное
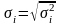 :
:
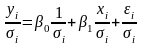 .
Обозначим
.
Обозначим
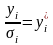 ,
,
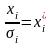 ,
,
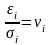 ,
,
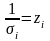 ,
получим уравнение регрессии без
свободного члена, но с дополнительной
объясняющей переменной
,
получим уравнение регрессии без
свободного члена, но с дополнительной
объясняющей переменной
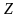 и с преобразованным отклонением
и с преобразованным отклонением
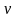 ,
для которого выполняется условие
гомоскедастичности:
,
для которого выполняется условие
гомоскедастичности:
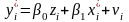 .
Таким образом ВМНК включает в себя
следующие этапы:
.
Таким образом ВМНК включает в себя
следующие этапы:
Значения каждой пары наблюдений
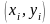 делят на известную величину
.
Тем самым наблюдениям с наименьшими
дисперсиями придаются наибольшие веса,
а с максимальными дисперсиями –
наименьшие веса. Это увеличивает
вероятность получения более точных
оценок.
делят на известную величину
.
Тем самым наблюдениям с наименьшими
дисперсиями придаются наибольшие веса,
а с максимальными дисперсиями –
наименьшие веса. Это увеличивает
вероятность получения более точных
оценок.По методу наименьших квадратов для преобразованных значений (
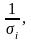
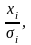
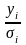 )
строится уравнение регрессии без
свободного члена с гарантированными
качествами оценок.
)
строится уравнение регрессии без
свободного члена с гарантированными
качествами оценок.
