
- •080105.65 ‑ Финансы и кредит;
- •080107.65 – Налоги и налогообложение;
- •080103.65 ‑ Национальная экономика
- •Введение 5
- •Введение
- •Глава 1. Корреляционный анализ §1.1. Корреляционный анализ в сильных шкалах
- •§1.2. Корреляционный анализ в слабых шкалах
- •Глава 2. Парный регрессионный анализ §2.1. Линейная модель парной регрессии
- •§2.2. Парный линейный регрессионный анализ в ms Excel
- •2.2.1. Добавление линейного тренда
- •2.2.2. Интерпретация линии тренда
- •2.2.3. Усовершенствование линии тренда
- •2.2.4. Инструмент анализа Регрессия
- •2.2.5. Интерпретация регрессии
- •2.2.6. Диаграммы регрессии
- •2.2.6. Регрессионные функции
- •§2.3. Парный нелинейный регрессионный анализ в ms Excel
- •2.3.1. Полиномиальное приближение
- •2.3.2. Логарифмическое приближение
- •2.3.3. Показательное приближение
- •2.3.4. Экспоненциальное приближение
- •Глава 3. Множественный линейный регрессионный анализ
- •§3.1. Спецификация модели. Отбор факторов при построении уравнения множественной регрессии
- •§3.2. Метод наименьших квадратов (мнк). Свойства оценок на основе мнк
- •§3.3. Проверка существенности факторов и показатели качества регрессии
- •§3.4. Линейные регрессионные модели с гетероскедастичными остатками
- •§3.5. Обобщенный метод наименьших квадратов (омнк)
- •§3.6. Регрессионные модели с переменной структурой (фиктивные переменные)
- •Решение
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Глава 4. Множественный линейный регрессионный анализ средствами ms Excel
- •§4.1. Интерпретация результатов регрессии
- •Значимость коэффициентов
- •Интерпретация регрессионных статистик
- •Интерпретация анализа дисперсии
- •§4.2. Анализ остатков
- •§4.3. Использование линии тренда для прогноза
- •Интерпретация прогноза
- •Глава 5. Гетероскедастичность и автокорреляция
- •§5.1. Обнаружение гетероскедастичности
- •Графический анализ остатков
- •Тест ранговой корреляции Спирмена
- •Тест Голдфелда-Квандта
- •§5.2. Методы смягчения проблемы гетероскедастичности
- •Дисперсии отклонений известны (метод взвешенных наименьших квадратов)
- •5.2.2. Дисперсии отклонений неизвестны
- •§5.3. Автокорреляция
- •Суть и причины автокорреляции
- •Обнаружение автокорреляции
- •Математико-статистические таблицы в.1. Таблица значений -критерия Фишера при уровне значимости
- •В.2. Критические значения -критерия Стьюдента при уровне значимости 0,10, 0,05, 0,01 (двухсторонний)
- •В.3. Значения статистик Дарбина-Уотсона при 5%-ом уровне значимости
- •Список основной литературы
- •Александр Леонидович осипов Евгений Алексеевич рапоцевич практикум по эконометрике
- •080105.65 ‑ Финансы и кредит;
- •080107.65 – Налоги и налогообложение;
- •080103.65 ‑ Национальная экономика
2.3.2. Логарифмическое приближение
В логарифмической модели
уравнение линии тренда имеет следующий
вид
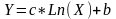 ,
где
,
где
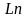 - натуральный логарифм. Так как логарифм
определен только для положительных
,
то значения независимой переменной
должны быть положительными. Если же
среди значений
имеются нулевые или отрицательные, то
на вкладке Тип окна Линии тренда
пиктограмма Логарифмическая будет
выделена серым. Чтобы обойти это
ограничение, можно добавить какое-либо
число ко всем
.
Результаты добавления логарифмической
линии тренда на график стоимости объектов
недвижимости приведены на рис. 2.19.
- натуральный логарифм. Так как логарифм
определен только для положительных
,
то значения независимой переменной
должны быть положительными. Если же
среди значений
имеются нулевые или отрицательные, то
на вкладке Тип окна Линии тренда
пиктограмма Логарифмическая будет
выделена серым. Чтобы обойти это
ограничение, можно добавить какое-либо
число ко всем
.
Результаты добавления логарифмической
линии тренда на график стоимости объектов
недвижимости приведены на рис. 2.19.

Рис. 2.19. Логарифмическая линия тренда
Повторяя последовательность шагов, описанную в разделе 2.3.1, получим более полные оценки регрессии в логарифмической модели с помощью инструмента анализа Регрессия. На рис. 2.20 представлены результаты инструмента регрессии после удаления части, относящейся к анализу дисперсии. По сравнению с линейной моделью, рассмотренной в разделе 2.2., данная логарифмическая модель имеет меньшую стандартную ошибку и большее . В соответствии с этим логарифмическая модель несколько лучше линейной.
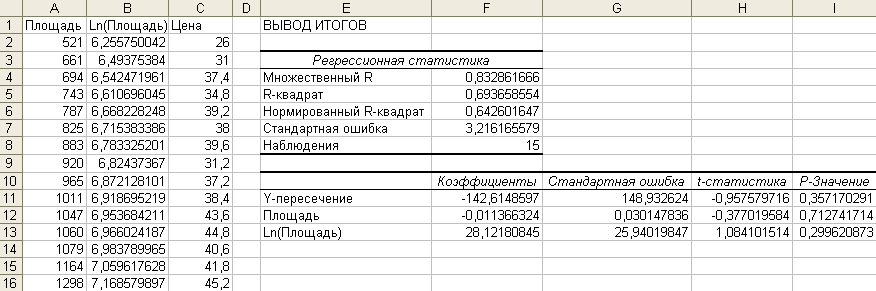
Рис. 2.20. Результаты применения логарифмической регрессии
Для осуществления прогноза
средней стоимости в логарифмической
модели введите значение Площади в ячейку
(например, А17) и формулу для вычисления
логарифма площади
 в ячейку В17. Затем постройте формулу
для предсказанной цены и поместите
=F12+F13*B17
в ячейку С17.
в ячейку В17. Затем постройте формулу
для предсказанной цены и поместите
=F12+F13*B17
в ячейку С17.
2.3.3. Показательное приближение
В показательной модели линия
тренда имеет следующее уравнение
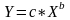 .
MS Excel
выполняет логарифмическое преобразование
исходных данных
и
для определения подобранных значений,
поэтому как зависимые, так и независимые
переменные должны быть положительными.
Если же среди значений
или
имеются нулевые или отрицательные, то
на вкладке Тип окна Линии тренда
пиктограмма Показательная будет выделена
серым. Чтобы обойти это ограничение,
можно добавить какое-либо число ко всем
и
.
Результаты добавления показательной
линии тренда на график стоимости объектов
недвижимости приведены на рис. 2.21.
.
MS Excel
выполняет логарифмическое преобразование
исходных данных
и
для определения подобранных значений,
поэтому как зависимые, так и независимые
переменные должны быть положительными.
Если же среди значений
или
имеются нулевые или отрицательные, то
на вкладке Тип окна Линии тренда
пиктограмма Показательная будет выделена
серым. Чтобы обойти это ограничение,
можно добавить какое-либо число ко всем
и
.
Результаты добавления показательной
линии тренда на график стоимости объектов
недвижимости приведены на рис. 2.21.
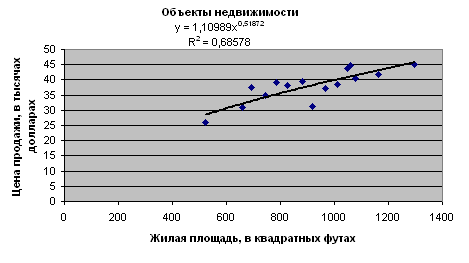
Рис. 2.21. Линия тренда в показательной модели
При добавлении показательной
линии тренда MS Excel
не пытается найти значения
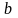 и
и
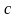 ,
минимизирующих сумму квадратов отклонений
фактических
и предсказанных. Вместо этого берется
логарифм от обеих частей формулы, что
может быть записано так
,
минимизирующих сумму квадратов отклонений
фактических
и предсказанных. Вместо этого берется
логарифм от обеих частей формулы, что
может быть записано так
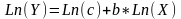 ,
а затем применяется обычная линейная
регрессия для зависимой переменной
,
а затем применяется обычная линейная
регрессия для зависимой переменной
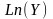 и независимой
и независимой
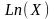 .
То есть MS Excel
определяет смещение и наклон, минимизирующие
сумму квадратов отклонений между
фактическими
и предсказанными
по формуле
.
То есть MS Excel
определяет смещение и наклон, минимизирующие
сумму квадратов отклонений между
фактическими
и предсказанными
по формуле
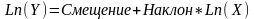 .
.
Таким образом, значение Смещения
соответствует
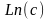 ,
а
в формуле равно Exp(смещение).
Значение Наклона соответствует
в формуле.
,
а
в формуле равно Exp(смещение).
Значение Наклона соответствует
в формуле.
Следующая последовательность шагов описывает получение более полных характеристик регрессии для показательной модели с помощью инструмента анализа Регрессия.
Введите данные в столбцы А и В, как показано на рис. 2.22.
Введите метку Ln(Площадь) в ячейку С1. Выделите ячейку С2 и введите формулу =Ln(А2).
Введите метку Ln(Цена) в ячейку D1. Выделите ячейку D2 и введите формулу =Ln(B2).
Скопируйте формулу в остальные ячейки, выделив C2 и D2 и дважды щелкнув по маркеру заполнения в правом нижнем углу ячейки D2. Значения логарифма появятся в столбцах С и D.
В меню Сервис выберите Анализ данных. В диалоговом окне Анализа данных выберите пункт Регрессия и нажмите ОК. Появится диалоговое окно Регрессии.
Входной интервал : укажите на листе или введите ссылки на диапазон со значениями зависимой переменной (D1:D16), включая метку в первой строке.
Входной интервал : укажите на листе или введите ссылки на область со значениями независимой переменной (С1:С16), включая метку в первой строке.
Метки: отметьте этот пункт, так как метки включены во входные интервалы для и .
Не выбирайте опции Константа – ноль или Уровень надежности.
Параметры вывода: щелкните по кнопке Выходной интервал, выделите строку справа и укажите или введите ссылку на левый верхний угол области шириной в 16 столбцов, куда будут помещены результаты (F1). Можно включить опции для получения Остатков. Затем нажмите ОК.
На рис.2.22 представлены результаты регрессии после удаления части, относящейся к анализу дисперсии. Значения - квадрат и Стандартной ошибки нельзя прямо сравнивать со значениями, полученными в линейной модели, так как здесь - квадрат является долей дисперсии , выраженной через в линейной модели, а Стандартная ошибка выражается в тех же единицах измерения, что и .
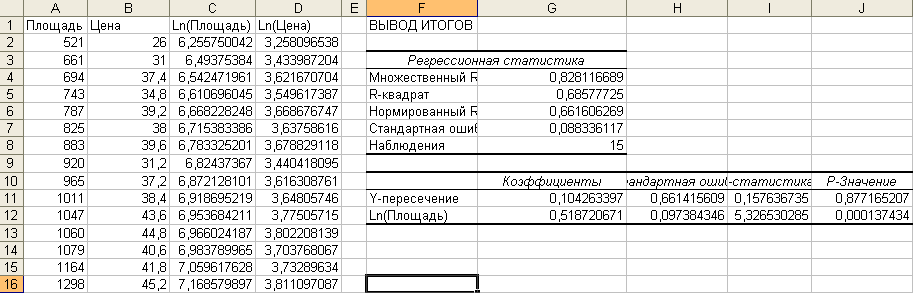
Рис. 2.22. Результаты применения показательной регрессии
Чтобы определить параметр формулы показательной модели, выделите ячейку G14 и введите формулу =EXP(G12). Для осуществления прогноза средней стоимости в показательной модели введите значение Площади в ячейку (например, А17). Затем постройте формулу для предсказанной цены (поместите =G14*A17^G13 в ячейку В17).
