§2.3. Парный нелинейный регрессионный анализ в ms Excel
В данном разделе описываются четыре способа моделирования нелинейной зависимости двух переменных: полиномиальной, логарифмический, показательный и экспоненциальный. Для каждого способа описывается добавление линии тренда на график, а также применение инструмента анализа Регрессии к преобразованным переменным для получения дополнительных характеристик. Общий подход добавления линии тренда состоит в следующем. Сначала строится график. Данные на листе располагаются так, чтобы столбец с данными был слева, а - справа. Выделите данные и и постройте точечную диаграмму с помощью Мастера диаграмм. Затем щелкните по точке данных на диаграмме, чтобы выделить ряд данных и выберите Добавить линию тренда в меню Диаграмма или щелкните правой кнопкой по ряду данных и выберите Добавить линию тренда в контекстном меню. Верхняя часть вкладки Тип диалогового окна Линия тренда представлена на рис. 2.6. Для получения линии тренда, описываемой в этом разделе, выберите соответствующий тип (полиномиальной, логарифмический, показательный или экспоненциальный) и на вкладке Параметры отметьте пункты Показать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации .
2.3.1. Полиномиальное приближение
На рис. 2.17 приведены результаты приближения квадратичной функцией. Значение =0,68, что немного лучше, чем для линейного тренда, у которого =0,66.
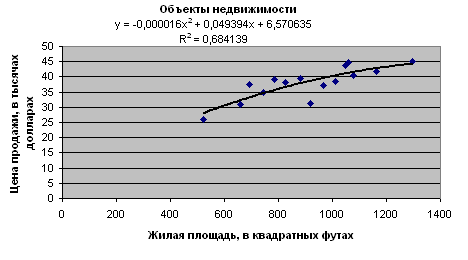
Рис. 2.17. Полиномиальная линия тренда
Следующая последовательность шагов описывает получение более полных характеристик регрессии для квадратичной модели.
Введите данные в столбцы А и С, как показано на рис. 2.18. Если Площадь и Стоимость уже введены в столбцы А и С, то выделите столбец В и выберите Добавить ячейки в контекстном меню. Введите метку Площадь^2 в ячейку В1.
Выделите ячейку В2 и введите формулу =А2^2. Скопируйте формулу в остальные ячейки столбца В, выделив В2 и дважды щелкнув по маркеру заполнения в правом нижнем углу. Квадраты значений появятся в столбце В.
В меню Сервис выберите Анализ данных. В диалоговом окне Анализа данных прокрутите список, выберите пункт Регрессия и нажмите ОК. Появится диалоговое окно Регрессии.
Входной интервал : укажите или введите ссылки на область со значениями зависимой переменной (С1:С16), включая метку в первой строке.
Входной интервал : укажите или введите ссылки на область со значениями независимой переменной (А1:А16), включая метку в первой строке.
Метки: отметьте этот пункт, так как метки включены во входные интервалы для и .
Не выбирайте опции Константа – ноль или Уровень надежности.
Параметры вывода: щелкните по кнопке Выходной интервал, выделите строку справа и укажите или введите ссылку на левый верхний угол области шириной в 16 столбцов, куда будут помещены результаты (Е1). Можно включить опции для получения Остатков. Затем нажмите ОК.
На рис. 2.18 приведены результаты регрессии после уничтожения части, относящейся к анализу дисперсии. По сравнению с линейной моделью, описанной в разделе 2.2., данная квадратичная модель имеет немного большую стандартную ошибку и немного больший . Исходя из этого, можно сказать, что квадратичная модель не лучше линейной.
Рис. 2.18. Результаты для полиномиальной регрессии
Чтобы осуществить прогноз средней цены в квадратичной модели, введите значение Площади в ячейку (например, А17) и формулу для Площади^2 (=А17^2 в ячейку В17). Затем постройте формулу для предсказанной ценны (введите =F12+F13*A17+F14*B17 в ячейку С17).