
Статический расчет трехшарнирной арки
Трехшарнирная арка представляет собой статически определимую распорную систему, состоящую из двух полуарок, соединенных между собой и поверхностью земли шарнирами. Опорные шарниры А и В обычно называют пятовыми, а средний С - ключевым (рис. 16).
Характерной особенностью распорных систем является наличие горизонтальных составляющих опорных реакций (распоры) при действии вертикальной нагрузки.
Трехшарнирные арки могут иметь опорные шарниры на одном и разных уровнях. Одна из шарнирно-неподвижных пятовых опор может быть заменена шарнирно-подвижной с вертикальным опорным стержнем. В этом случае для обеспечения геометрической неизменяемости вводится затяжка-стержень, который воспринимает распор (рис. 17).
Для трехшарнирной арки с опорами в одном уровне характерными величинами являются длина пролета l (расстояние между опорами А и В), размеры левой и правой полуарок l1 и l2, стрела подъема f.
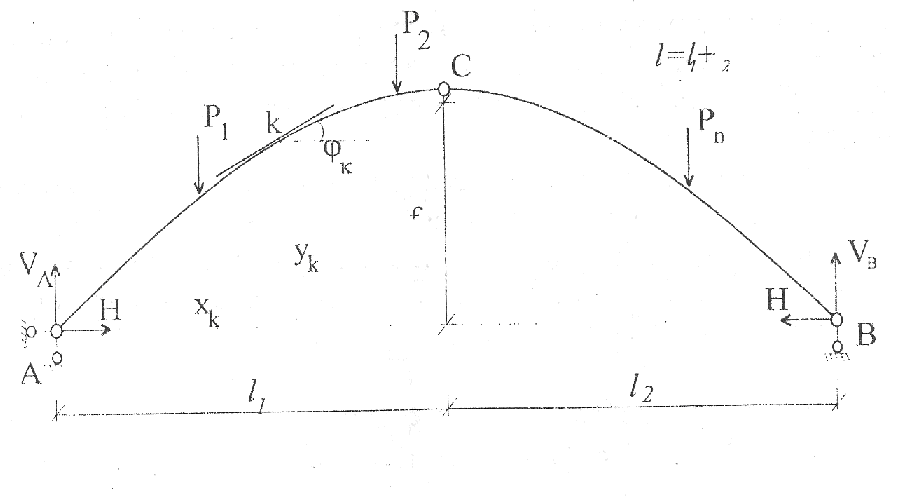
Рис. 16
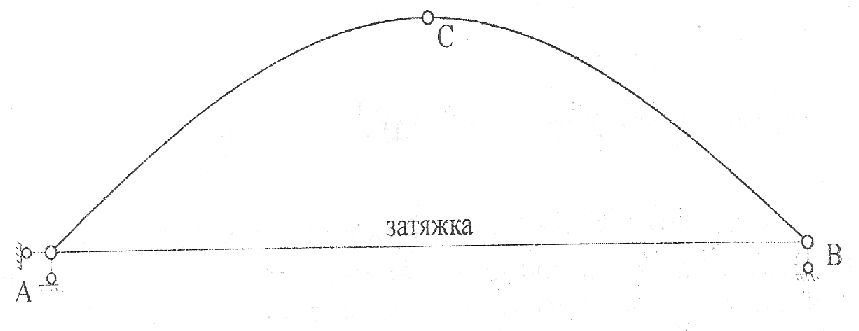
Рис. 17
Сечение k определяется координатами хk, уk, а также углом наклона касательной к оси арки φk. В сечениях трехшарнирной арки возникают изгибающие моменты, перерезывающие и продольные усилия. Изгибающий момент считается положительным, если растягивается нижнее волокно арки.
Положительно определенная поперечная сила поворачивает часть конструкции, на которую действует, по часовой стрелке. Положительная продольная сила растягивает ось арки.
Аналитический расчет трехшарнирной арки включает в себя определение опорных реакций VA, VB, H, определение внутренних усилий Mk, Qk, Nk в произвольном сечении, построение эпюр Mk, Qk, Nk. Опорные реакции и внутренние усилия в арке определяются из соотношений:
![]()
![]()
![]()
![]()
![]()
![]()
Здесь через V°A, Q°B, M°k, Q°k обозначены соответствующие величины для однопролетной балки, лежащей на шарнирных опорах, перекрывающий пролет l и загруженных такой же поперечной нагрузкой, что и арка.
Если сечение К расположено справа от шарнира С, то в формулах (6) нужно перед слагаемым с множителе SIN(X) поменять знак на противоположный.
На рис. 18 представлена расчетная схема трехшарнирной арки.
Кинематический анализ арки выполняется аналогично соответствующему разделу п. 1.1. Арка составлена из двух дисков АС и BC и имеет в своей структуре один шарнир C и четыре связи (шарнирно-неподвижные опоры A и B). Таким образом:
W = 3D – 3Ш - C0 = 3∙2 - 2∙1- 4 = 0.
Далее, два упомянутых диска AC и BC соединены между собой и с основанием тремя шарнирами A, B, C, которые не лежат на одной прямой.
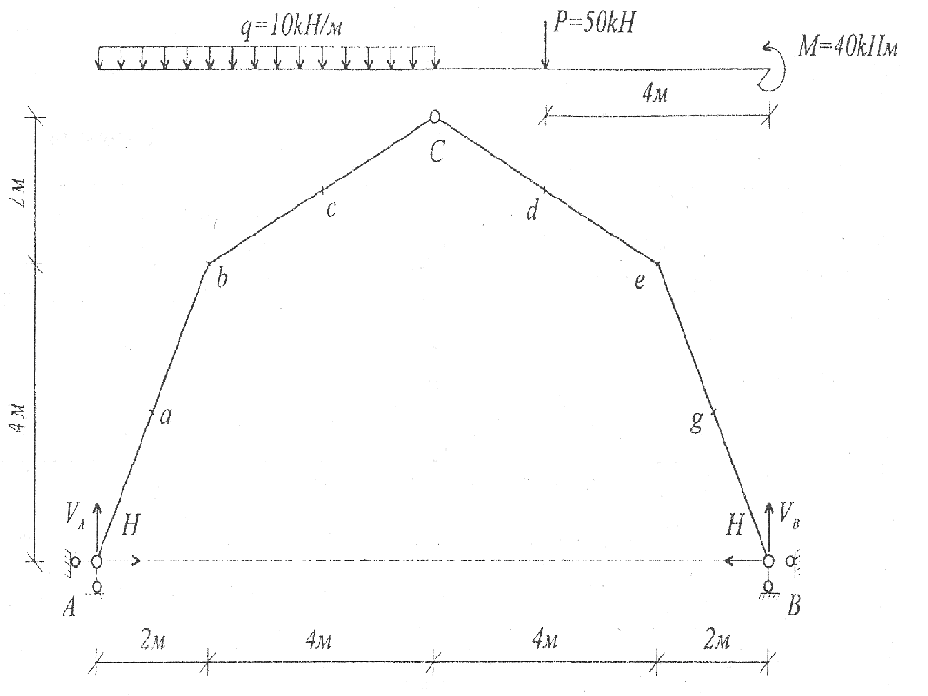
Рис. 18
Определяем опорные реакции в арке:
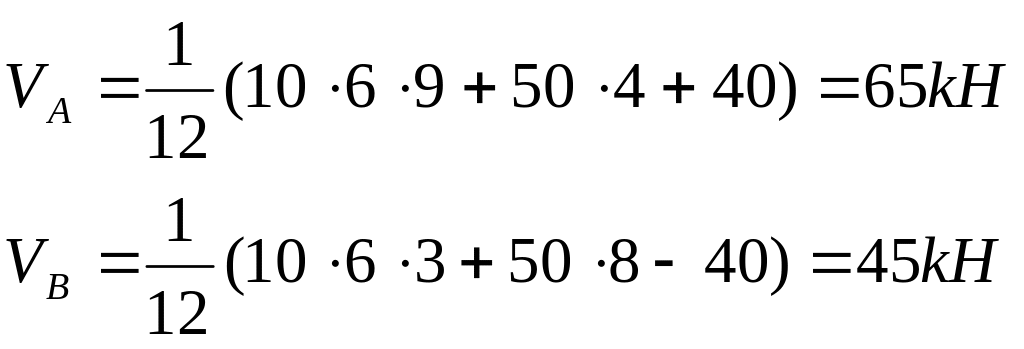
![]() (равновесие
левой полуарки)
(равновесие
левой полуарки)
![]() (равновесие
правой полуарки)
(равновесие
правой полуарки)
Результаты последующего расчета оформлены в табл. 2.
Таблица 2
N
|
Координаты [М] |
φk
|
sin φk
|
cos φk |
[kH∙м]
|
[kH] |
Mk [kН∙м] |
Qk [kH] |
Nk [kH] |
|
хк |
yк |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
А |
0 |
0 |
63,43 |
0,8944 |
0,4472 |
0 |
65 |
0 |
-2,236 |
-73,788 |
а |
1 |
2 |
63,43 |
0,8944 |
0,4472 |
60 |
55 |
-10 |
-6,708 |
-64,844 |
b- |
2 |
4 |
63,43 |
0,8944 |
0,4472 |
110 |
45 |
-30 |
-11,18 |
-56,08 |
B+ |
2 |
4 |
26,57 |
0,4472 |
0,8944 |
110 |
45 |
-30 |
24.596 |
-51,428 |
c |
4 |
5 |
26,57 |
0,4472 |
0,8944 |
180 |
25 |
5 |
6,708 |
-42,4841 |
С- |
6 |
6 |
26,57 |
0,4472 |
0,8944 |
210 |
5 |
0 |
-11,18 |
-33,54 |
C+ |
6 |
6 |
-26,57 |
-0,4472 |
0,8944 |
210 |
5 |
0 |
20,124 |
-29,068 |
d
|
8
|
5
|
-26,57
|
-0,4472
|
0,8944 |
220
|
5 |
45
|
20,124 |
-29,068 |
-45 |
-24,596 |
-51,428 |
||||||||
e- |
10 |
4 |
-26,57 |
-0,4472 |
0,8944 |
130 |
-45 |
-10 |
-24,596 |
-51,428 |
e+ |
10 |
4 |
-63,43 |
-0,8944 |
0,4472 |
130 |
-45 |
-10 |
11,18 |
-55,90 |
g |
11 |
2 |
-63,43 |
-0,8944 |
0,4472 |
85 |
-45 |
15 |
11,18 |
-55,90 |
В |
12 |
0 |
-63,43 |
-0,8944 |
0,4472 |
40 |
-45 |
40 |
11,18 |
-55,90 |
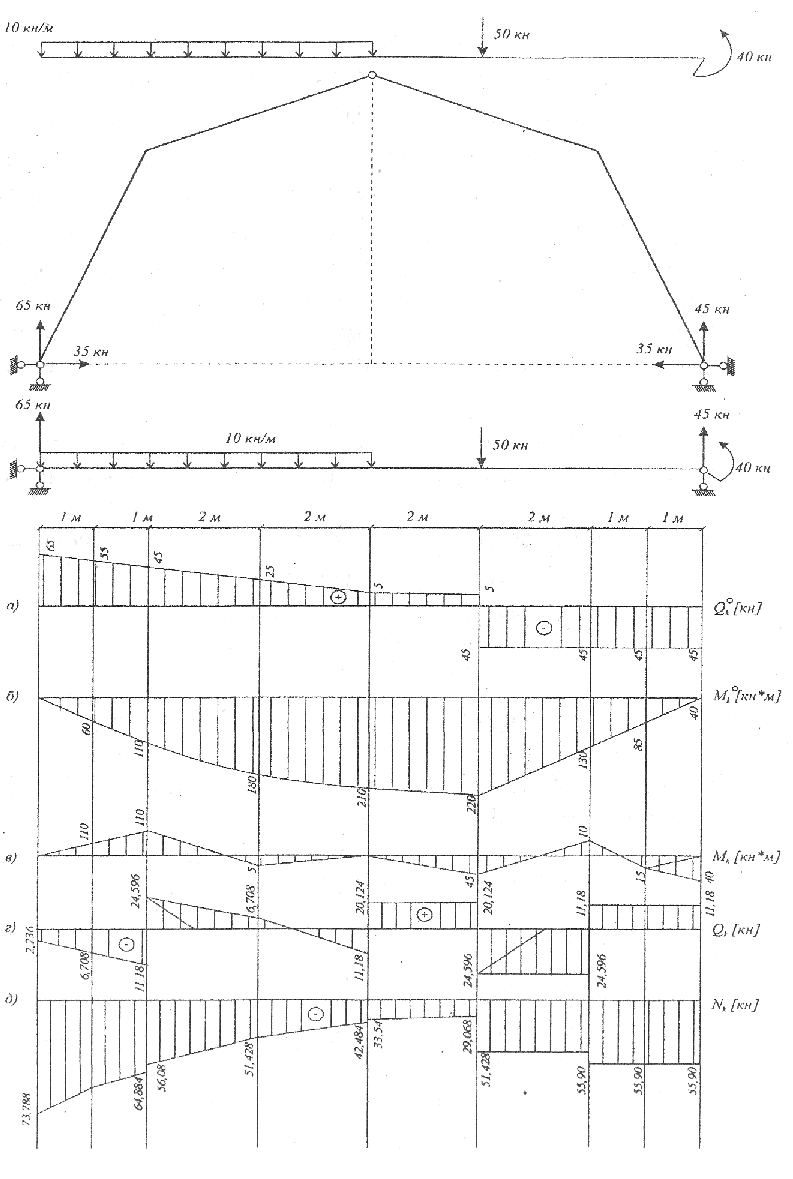
Рис. 19
Сечения назначены в середине и на концах каждого из стержней, образующих ось арки (см. обозначения на рис. 18). На рис. 19 (а, б) представлены эпюры и для соответствующей балки, перекрывающей данный пролет и несущей заданную поперечную нагрузку. На рис. 18(в, г, д) представлены эпюры внутренних усилий Mk, Qk, Nk в исходной трехшарнирной арке, которые построены в отрезках прямых линий. Точность в очертаниях эпюр зависит от количества назначенных сечений. Скачки на эпюрах Qk и Nk при переходе через сечения в, с и е объясняются резким изменением значений тригонометрических функций угла φk.
Обращаем внимание на существенное уменьшение значений ординаты арочных эпюр Мk и Qk по сравнению с балочными и .
Подберем поперечные сечения арки и балки из условия прочности.
![]()
Двутавровый профиль №50 по ГОСТ 8239-72: Wx=1589 см3; F=100 см2; 1х=39727см4.
Для арки необходима проверка условия прочности с учетом действия продольной силы:
![]()
Превышение над значением [σ]=160 МПа составляет 7,19%.
Поэтому, для арки назначаем следующий номер профиля - 24а, для которого Wx=317 см3; F=37,5 см2; Ix=3800 см4.
Сравним вес запроектированных конструкций:
Q6 = 7,85 - 100∙12∙10-3 =9,42 kH
QA = 7,85∙37,5∙4∙ 4,47∙10-3 = 5,26 kH
Таким образом, вес арки составляет 55,9% от веса балки.
