Розв’язування 5.6

1. Яскравість (В) поверхні, яка розсіює світло за законом Ламберта, зв’язана з її освітленістю (Е) співвідношенням:

(1)

де – коефіцієнт розсіювання білого екрана.

Таким чином, яскравість (В) зображення на екрані пропорційна його освітленості.

В свою чергу, освітленість зображення, яке отримане за допомогою лінзи, пропорційне величині ( ), як це видно з формули:

(2)

(задача 5.4; формула (11)).

Значить, яскравість (В) зображення на екрані пропорційна квадрату діаметра лінзи.

2. На мал. 5.6 – предмет; – його зображення; – тілесний кут, в якому розповсюджується світловий потік , що випромінюється елементом поверхні предмета і падає на лінзу; – тілесний кут, в якому розповсюджується той же самий світловий потік, падаючи на відповідний елемент зображення (втратами світла в лінзі нехтуємо). Очевидно, що під таким же кутом промені, створивши елемент зображення будуть розходитися. Відмітимо, що зображення , на відміну від предмета видно не зі всіх боків.

Для того, щоб спостерігач бачив елемент зображення, його око має знаходитися всередині тілесного кута .Таким чином, лише в напрямку одного із променів, який лежить в середині кута , має зміст говорити про яскравість (В) елемента зображення . В інших напрямках його яскравість рівна нулю.

Для того, щоб знайти величину (В) врахуємо, що, згідно визначення яскравості і сили світла, яскравість вимірюється світловим потоком, який випромінюється одиницею площі видимої світної поверхні всередині одиничного тілесного кута. Тому яскравість елемента можна записати:

(1)

Але відомо, що при зміні діаметра об’єктива величина та (мал.5.6) будуть змінюватися пропорційно , а відношення залишиться постійним. Таким чином, яскравість (В) зображення (формула (1), яке будемо розглядати безпосередньо, не залежить від діаметра лінзи.

Зауваження. Нехтуючи втратами світла в лінзі, можна показати, що яскравість (В) зображення незалежно від діаметра об’єктива рівна яскравості ( ) предмета, яка визначається співвідношенням:

(2)

Але відомо, що величини , , , можна виразити через та – відстані від лінзи до предмета та зображення:

(3)

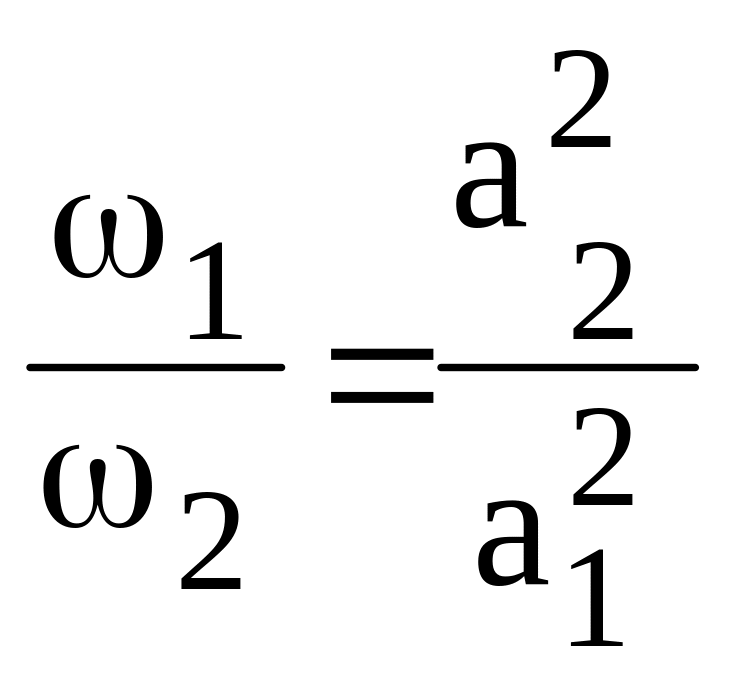(4)

Звідси маємо:

, або (5)

Звідси випливає (див. формулу (1, 2) рівність яскравостей .

Задача 5.7 (22-14, Фірганг, С.263)

Я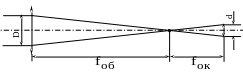 к зміниться освітленість зображення протяжного об’єкта (наприклад, планети) на сітківці ока при переході від спостереження неозброєним оком до спостереження в телескоп із збільшенням (Г). Діаметр об’єктива телескопа (D). Розглянути два випадки: 1) Г> ; 2) Г< ; де – діаметр зіниці. Втратами світла в телескопі знехтувати.

Мал. 5.7