§. Формула Ньютона-Лейбница.

Пусть fR_I, aI, xI. Рассмотрим функцию: .

Прежде отметим два простых факта

а). Непрерывность интеграла, как функции верхнего предела:

.

б) Дифференцируемость интеграла, как функции верхнего предела: fR_I , f непрерывна в x₀I, то дифференцируема в точке x₀, причём производная по верхнему пределу совпадает со значением подынтегральной функции в точке x₀: .

= = = =

= .

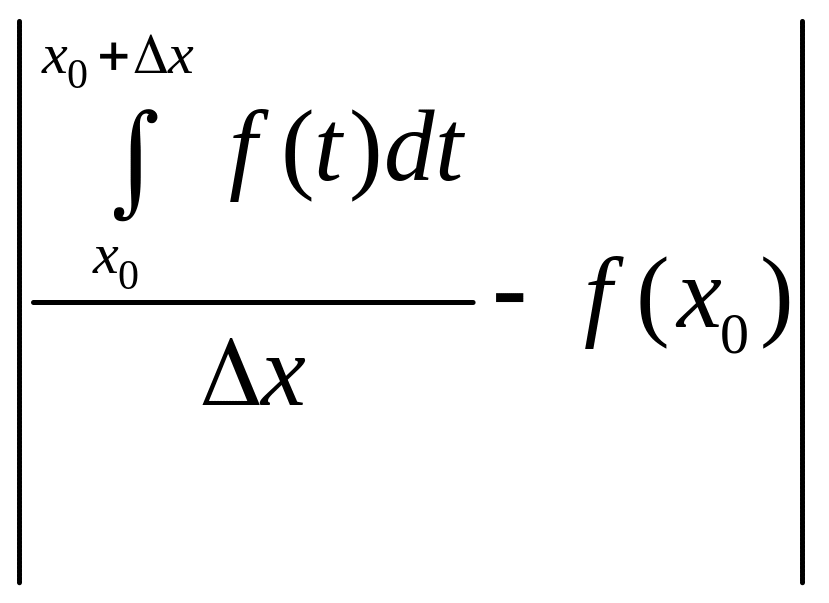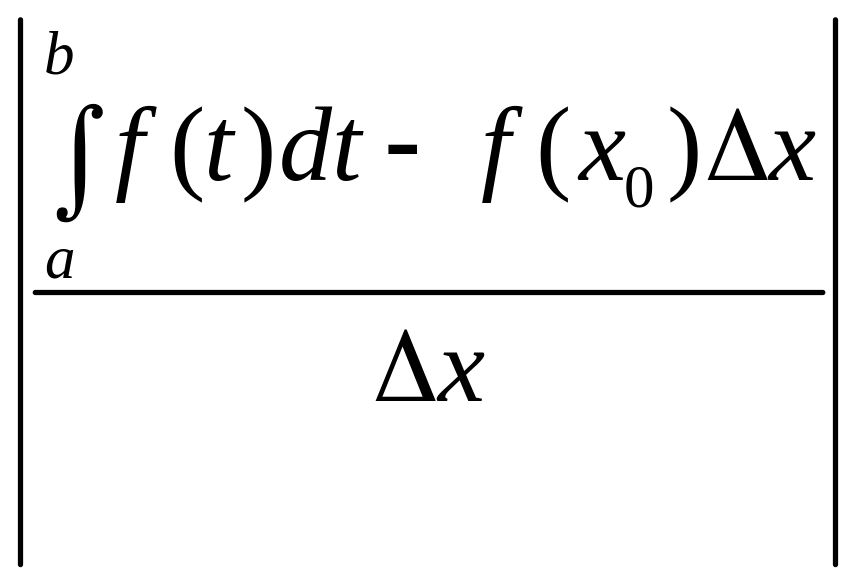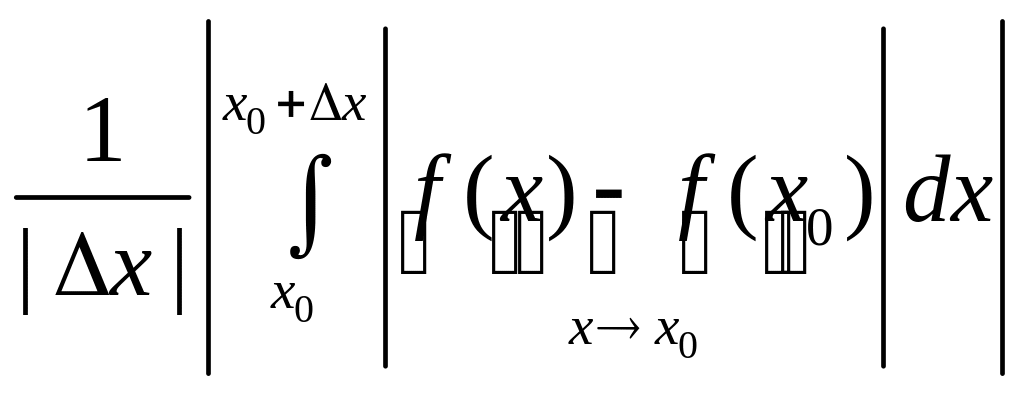
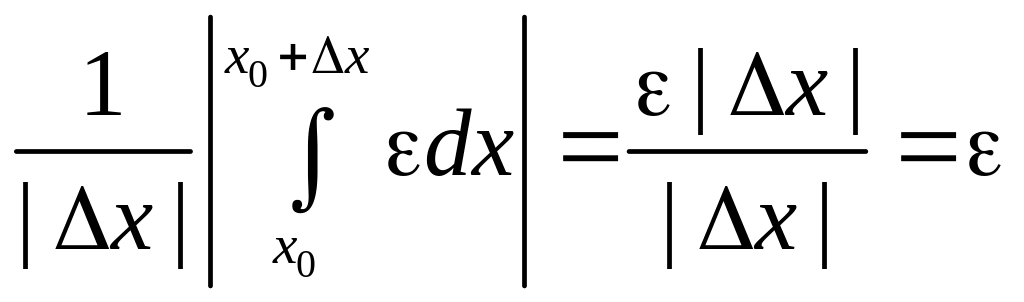т.е. .

Далее

в) Существование первообразной у непрерывной функции. Если f (x) непрерывна на промежутке, то у неё существует первообразная, которая с точностью до постоянного слагаемого является определённым интегралом от этой функции с переменным верхним пределом

F (x) = f(x) xI, где f (x) непрерывна по условию.

г) Обобщённая первообразная. Функция F(x) называется обобщённой первообразной для

f (x) на I, если F (x) = f (x) всюду на I, кроме может быть не более чем счётного множества точек. Пример т.е. | x | – обобщённая первообразная для sgn x.

Обобщённые первообразные отличаются не более, чем на постоянное слагаемое:

 .

Т. Всякая непрерывная на некотором промежутке функция, производная которой существует и равна нулю всюду кроме, не более чем счётного числа точек является константой. ▲

«

канторова-лестница»

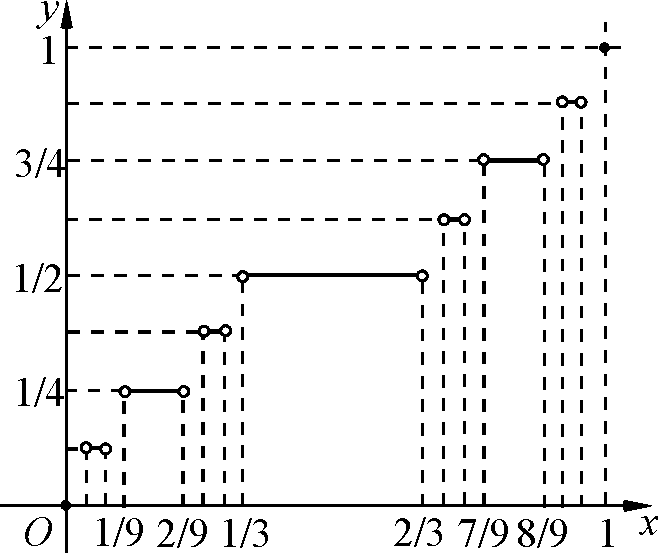
F (x) = 0 xС С – множество точек разрыва т.к. (С) = 0, то F (x) = 0 п.в. на [0, 1] по F(x) не константа (т.е. не более чем счётное число точек и множество лебеговой меры нуль не одно и тоже).

д). Если функция f (x) на I имеет обобщённую первообразную,то [a, b]  I

.

Записанная выше формула и есть формула Ньютона–Лейбница, связывающая интегральное исчисление с дифференциальным и, позволяющая вычислять определенные интегралы с помощью первообразных.

 В равенстве положим x = a   C = – (a) 

 или, что тоже самое .▲

§. Дифференцирование определённого интеграла, пределы которого дифференцируемые функции.

Вспоминая цепное правило дифференцирования сложной функции, можно написать следующую формулу . ▲.

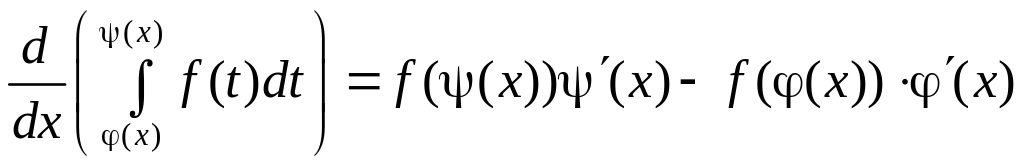§. Замена переменных в определённом интеграле.

П

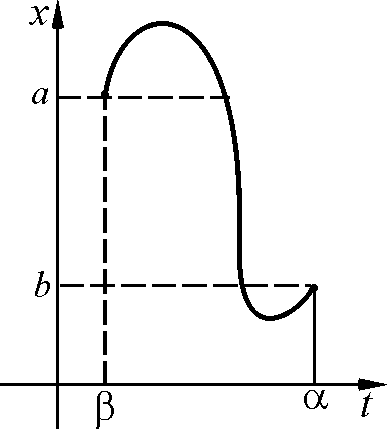
усть fR_{[a, b]} и на промежутке x[a, b] рассматривается . Кроме того, пусть задана функция x = (t) t[, ], причем () = a, () = b

и функция строго монотонна и непрерывно дифференцируема на промежутке . Тогда справедлива формула, именуемая формулой замены переменной в определенном интеграле

. ▲.

На иллюстрации сделана попытка пояснить необходимость монотонности функции x = (t).

§. Примеры.

1. Найти .

а). Формальное применение формулы Ньютона–Лейбница дает

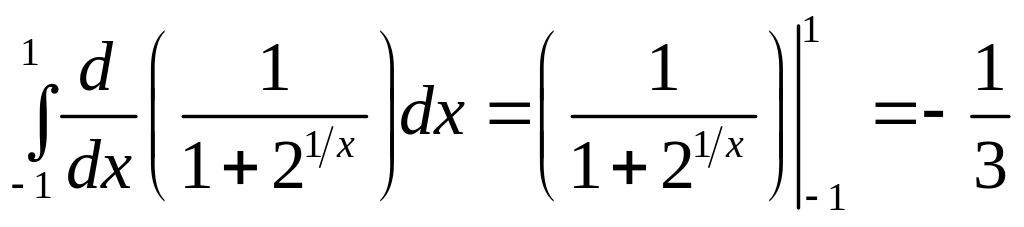, что само по себе удивительно, ибо интеграл от неотрицательной функции оказался отрицательным.

б). Давайте более аккуратно подойдем к нахождению первообразной функции. Для этого найдем первообразную отдельно для x больших и для x меньших нуля.

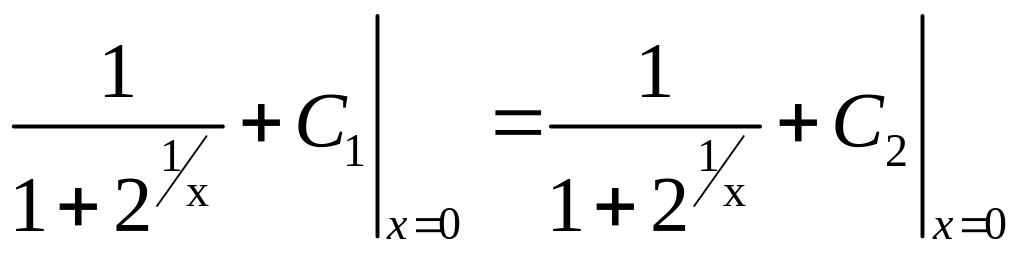
Получим для , и для . Чтобы найти первообразную на всем промежутке надо потребовать чтобы найденная первообразная была непрерывна, т.е. чтобы  . Значит первообразная подынтегральной функции на промежутке имеет вид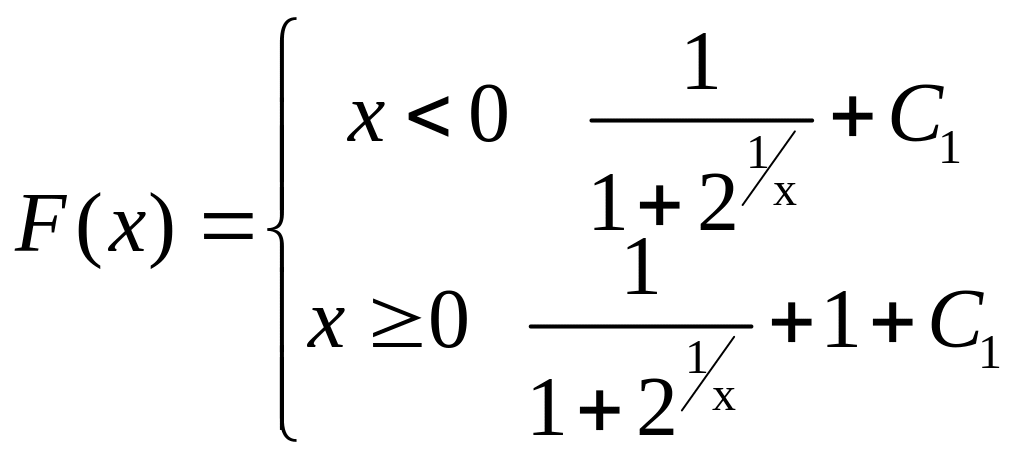 и теперь применение формулы Ньютона– Лейбница дает правильный результат .

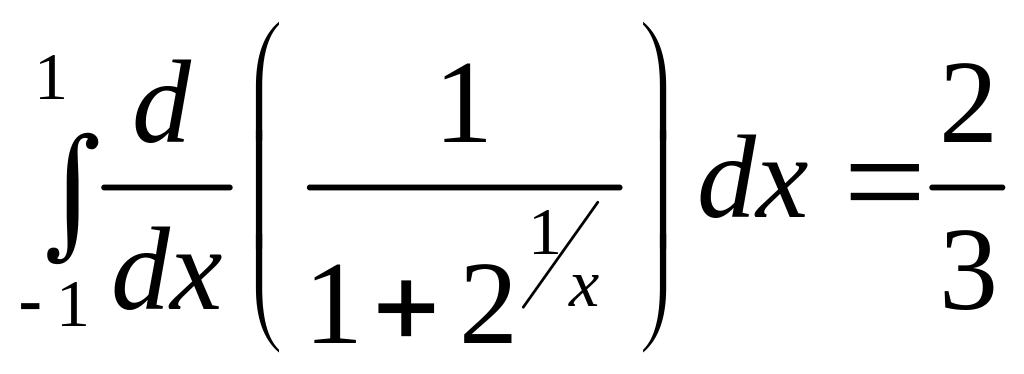2. . Формально выполняя замену переменной получим что , что очевидно неверно. Для получения правильного результата необходимо учесть, что функция разрывна при и следовало бы написать

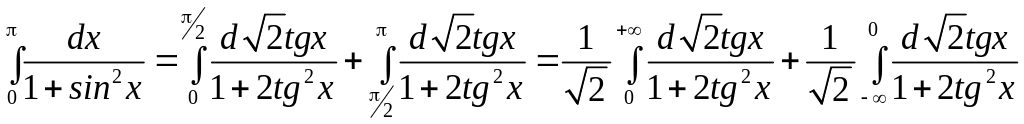, однако на этом пути нас ожидает еще одна неприятность принципиального порядка. Идея определенного интеграла не может быть реализована для бесконечных промежутков интегрирования. Здесь мы вторгаемся в область несобственных интегралов, которые будут рассмотрены несколько позже.

Приведенные два примера показывают что, и при применении формулы Ньютона –Лейбница и при замене переменной в определенном интеграле следует быть очень осторожным.