§. Необходимое условие интегрируемости

Т. Функция, интегрируемая на некотором промежутке, необходимо ограничена на нём.

Множество функций, интегрируемых на промежутке, обозначается: R(I) или R_{[a, b]}.

Напоминание: Критерий Коши существования предела по базе функции

 .

∆ Докажем: ограничена на I. Так как функция интегрируема, то

От противного: Предположим, что не ограничена на I . Тогда не ограничена на некотором подпромежутке промежутка разбиения , т.е. при :

Это следует из интегрируемости функции .

Но, если выбрать разбиения и , отличающиеся только одной отмеченной точкой , для которых (это возможно, т.к. функция неограниченна) то получим: . Полученное противоречие доказывает теорему ▲

Но ограниченность – только необходимое условие интегрируемости, однако недостаточное. Например, функция Дирихле не интегрируема (хотя и ограниченна). В самом деле: 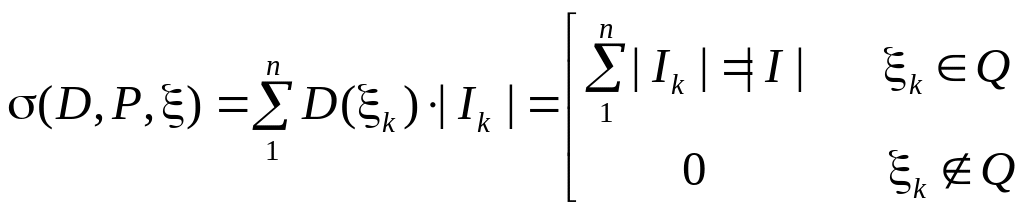, и, следовательно, предел интегральных сумм не существует.

§ Суммы и интегралы Дарбу

Рассмотрим разбиение промежутка [a, b] – Р_{[a, b]}. Для каждого промежутка разбиения выберем

;

и построим суммы: и , называемые нижней и верхней суммами Дарбу.

При этом:

и , .

Нетрудно понять, что при измельчении разбиения не уменьшаются, а не увеличиваются: .

Таким образом, нижние суммы Дарбу при измельчении разбиении образуют монотонно возрастающую и ограниченную сверху, а верхние – монотонно убывающую и ограниченную снизу последовательности. По теореме Вейерштрасса каждая из этих последовательностей имеет предел при . Эти пределы называются нижним и верхним интегралами Дарбу.

,

и, кроме того, .

§ Критерий Дарбу интегрируемости функций по Риману

Т°. Функция f (x) интегрируема на промежутке [a, b], тогда и только тогда, когда её верхний и нижний интегралы Дарбу равны между собой.

  .

∆. а). Пусть функция интегрируема по Риману. Тогда

 .

Следовательно: и, в силу того, что и верхняя и нижняя суммы Дарбу есть частные случаи сумм Римана, получим . Переходя к пределу при получаем, что , т.е.

.

б). Пусть верхний и нижний интегралы Дарбу совпадают. Принимая во внимание, что и используя теорему о двух милиционерах, переходим к пределу при : ▲

Другие формулировки того же критерия:

*). Если интегрируема на , то .

*). Если интегрируема на , то .

§ Интегрируемость непрерывных и монотонных функций

Т°. Функция непрерывная на замкнутом промежутке интегрируема на нём.

.

Т°. Функция монотонная на замкнутом промежутке интегрируема на нём.

 .

∆ а). Пусть т.е. непрерывна  равномерно непрерывна на . Тогда , и получим:

и по критерию Дарбу , что и требовалось доказать.

б). Пусть f (x) монотонна на [a, b]. Например, монотонно возрастающая: .

Тогда: , что и требовалось доказать ▲