
Методическое указание по полупроводникам и диодам
.pdf
1.4.Полупроводниковые приборы
1.4.1.Полупроводниковые диоды
Основы физики полупроводников
Все твердые тела по их способности проводить электрический ток делятся на три широких класса: проводники (металлы), полупроводники и диэлектрики (изоляторы). В табл. 1.2 приведены данные по электропроводности различных классов веществ.
|
|
|
Таблица 1.2 |
|
|
Электропроводность твердых веществ |
|
||
Класс веществ |
Удельная |
|
Удельное электрическое |
|
|
электропроводность, См/см |
сопротивление, Ом·см |
||
Проводники |
> 104 |
|
< 10-4 |
|
Полупроводники |
104…10-10 |
|
10-4…1010 |
|
Диэлектрики |
< 10-10 |
|
> 1010 |
|
Удельная |
электропроводность σ – величина обратная удельному |
|||
электрическому |
сопротивлению |
σ =1 ρ , |
размерность |
которой |
[σ]=1 [ρ]=1 (Ом м)= См м. |
|
|
|
|
Такая классификация твердых тел по их способности проводить электрический ток относится ко времени первых опытов с электричеством и достаточно примитивна. При глубоком и систематическом изучении принципов электропроводности полупроводников было обнаружено, что их электропроводность отличается от электропроводности проводников не только количественно, но и качественно; было обнаружено, что полупроводники имеют больше общих свойств с диэлектриками.
1.Влияние температуры. Электропроводность полупроводников резко возрастает даже при небольшом увеличении температуры (до 5…6 % на 1 °C). Электропроводность металлов с ростом температуры падает, причем незначительно (доли процента на 1 °C).
2.Влияние примеси. Ничтожное введение примеси в полупроводник в размере 0,001 % может в 104 увеличить его электропроводность. Практически не влияет на электропроводность проводников.
3. Влияние света, ионизирующих излучений, энергетических воздействий. Перечисленные воздействия приводят к увеличению электропроводности полупроводников. Практически не влияет на электропроводность проводников.
Таким образом полупроводник – это вещество, удельная проводимость которого существенно зависит от внешних факторов.
Примеры полупроводниковых веществ: трехвалентные – бор (B), галлий (Ga), индий (In);
четырехвалентные – кремний (Si), германий (Ge), селен (Se); пятивалентные – фосфор (P), мышьяк (As), сурьма (Su); полупроводниковые соединения, образованные элементами 3-й и 5-й
групп периодической системы Менделеева (AIII – BV) – арсенид галлия
(GaAs), фосфид индия (InP).
Зонная теория твердого тела. В основе описания электропроводности твердых тел лежит квантовая теория энергетического спектра электронов в веществах. Причем ее простейший вариант, учитывающий наиболее важные особенности движения электронов в кристаллах, – зонная теория позволяет успешно интерпретировать различие электрических свойств материалов.
Согласно законам квантовой механики электроны в изолированных атомах могут находиться только в определенных энергетических состояниях, характеризуемых дискретным рядом значений энергии, называемых энергетическими уровнями. Причем согласно принципу Паули на каждом энергетическом уровне может находиться два электрона с разными спинами.
|
|
|
|
При объединении N атомов в кристалл |
|||
E |
|
|
из-за их взаимодействия последний |
||||
|
|
можно рассматривать как |
гигантскую |
||||
∆Ez |
|
||||||
|
|
|
молекулу, у которой электроны всех |
||||
Ez |
|
||||||
|
|
Разрешенная |
атомов обобществлены. Каждый из |
||||
|
|
||||||
|
|
зона |
энергетических |
уровней в |
кристалле |
||
|
|
|
|
размывается, превращается в полосу из |
|||
|
|
|
|
N |
уровней, |
которая |
образует |
|
|
Запрещенная |
разрешенную |
энергетическую зону |
|||
|
|
зона |
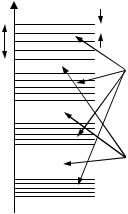
(рис. 1.32). Разрешенные зоны отделены |
||||
одна от другой диапазонами значений энергии, называемыми запрещенными энергетическими зонами, которые электроны не могут принимать в данной квантовомеханической системе.
Заполнение электронами разрешенных энергетических уровней происходит согласно распределению Ферми – Дирака, начиная с нижних уровней. Хотя структура энергетических зон дискретна, но ввиду близости уровней зоны оказываются квазинепрерывными. Расстояние между соседними уровнями в пределах разрешенной зоны гораздо меньше тепловой энергии электрона при комнатной температуре.

Пример. Расстояние между соседними энергетическими уровнями в разрешенной зоне ∆Ez (рис. 1.32).
Пусть ширина разрешенной зоны некоторого кристалла Ez ≈1эВ. Рассматриваем кристалл объемом V =1см3 . Плотность атомов в кристалле
N ≈1022 1 см3 . Электронвольт – несистемная единица измерения энергии, используемая в квантовой механике: 1эВ =1,6 10−19 Дж.
см3 . Электронвольт – несистемная единица измерения энергии, используемая в квантовой механике: 1эВ =1,6 10−19 Дж.
∆Ez ≈ |
Ez |
= |
|
|
1эВ |
|
=10−22 |
эВ. |
||
N V |
|
22 1 |
|
|
3 |
|||||
|
10 |
|
1см |
|
|
|||||
|
|
|
см |
3 |
|
|
|
|||
Статистическая функция Ферми – Дирака, описывающая вероятность fD (E) нахождения свободного электрона в энергетическом
состоянии E , имеет следующий вид
f |
|
|
+e |
(E −E f ) kT |
−1 |
(1.4.1) |
D |
(E)= 1 |
|
, |
|||
|
|
|
|
|
|
где E f |
– энергия Ферми или уровень Ферми, уровень энергии которой |
электрон |
может обладать с вероятностью fD (E f )=1 2 ; k T – средняя |
энергия |
теплового движения микрочастицы при температуре T ; |
k =1,38 10−23 Дж К – постоянная Больцмана; T – абсолютная температура,
К – постоянная Больцмана; T – абсолютная температура,
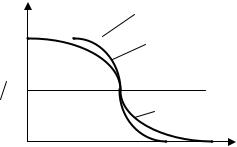
выраженная в кельвинах. На рис. 1.33 представлены графики зависимости fD = f (E) для различных температур.
Анализ выражения (1.4.1):
1. При T = 0 К вероятность заполнения уровней с энергиями меньше
энергии Ферми равна единице (рис. 1.33)
fD (E < E f )= 1+e(E −E f ) 0 −1 = (1+e−∞ )−1 = (1+0)−1 =1.
0 −1 = (1+e−∞ )−1 = (1+0)−1 =1.
При T = 0 К вероятность заполнения уровней с энергиями больше
энергии Ферми равна нулю (рис. 1.33)
fD (E > E f )= 1+e(E −E f ) 0 −1 = (1+e∞ )−1 = (1+∞)−1 = 0.
0 −1 = (1+e∞ )−1 = (1+∞)−1 = 0.
2. При T > 0 К повышается вероятность заполнения уровней с
энергиями выше энергии Ферми, и уменьшается вероятность заполнения уровней с энергиями меньше энергии Ферми (рис. 1.33).
При изучении электропроводности твердых тел рассматривают верхнюю из разрешенных зон, на подуровнях которой при температуре абсолютного нуля T = 0 К находятся электроны. Заряд будет переносится
только такими электронами, над уровнями которых располагаются свободные энергетические уровни. Приобретая дополнительную энергию за счет различных взаимодействий (увеличение температуры, воздействие
fD (E) |
|
|
T2 >T1 > 0 |
||||
|
|
T = 0 |
|||||
1 |
|
|
|
|
|
|
|
|
|
|
T1 |
||||
|
|
||||||
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T2 |
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
излучений и т.д.), электроны будут переходить на верхние свободные уровни, наличие которых связано с существованием соседних атомов, т.е. перемещаться от атома к атому.
Валентная зона – верхняя из разрешенных энергетических зон, все подуровни которой заполнены электронами при T = 0 К.
E f
Рис. 1.2
зоны проводимости Ec
Eg = Ec − Ev .
E |
Зона |
проводимости – |
|
разрешенная зона, |
расположенная |
|
над валентной. |
|
Ширина запрещенной зоны –
энергетический интервал между дном и потолком валентной зоны Ev
(1.4.2)
Зонные энергетические диаграммы различных веществ показаны на рис. 1.34. В металлах верхняя из разрешенных зон, на подуровнях которой находятся электроны при T = 0 К, заполнена частично (рис. 1.34,а). Эта зона
для металлов является зоной проводимости, все электроны которые находятся в этой зоне (а это валентные электроны) являются электронами проводимости, т.е. свободно могут перемещаться от атома к атому, а значит являются подвижными носителями заряда. Концентрация таких электронов (в случае одновалентного элемента) равна концентрации атомов в
металлической решетке n = Nm ≈1022 1 см3 . При изменении температуры
см3 . При изменении температуры
число свободных электронов в металле не изменяется. Уменьшение проводимости металлов с ростом температуры объясняется увеличением тепловых колебаний атомов решетки, на которых происходит рассеяние электронов. В металле уровень Ферми располагается чуть выше самого верхнего из подуровней, на котором находится электрон.
В полупроводниках при T = 0 К верхняя из разрешенных зон, на
подуровнях которой находятся электроны, полностью заполнена электронами (валентная зона) (рис. 1.34,б). Подуровни расположенной над ней разрешенной зоны (зоны проводимости) не содержат электронов при T = 0 К. Разделены валентная зона и зона проводимости запрещенной зоной
с шириной Eg ≤ 3K4 эВ. Таким образом при T = 0 К в полупроводниках
отсутствуют свободные носители заряда, поскольку электроны не могут переместиться на свободные уровни зоны проводимости, у них нет достаточно энергии. Только при повышении температуры, когда энергия электронов превысит Eg , некоторые из них попадают в зону проводимости и
становятся свободными носителями заряда. Чем выше температура, тем

больше электронов попадает в зону проводимости. Число свободных носителей в полупроводниках гораздо меньше, чем в металлах.
Уровень Ферми в собственных полупроводниках располагается в середине зоны проводимости.
|
Металлы |
Полупроводники |
|
Диэлектрики |
|
E |
Зона |
E |
Зона |
E |
Зона |
проводимости |
|
проводимости |
|||
|
проводимости |
|
|||
E f |
|
|
|
|
|
|
E f |
Eg <3K4 эВ E f |
Eg >3K4 эВ |
||
|
|
|
Валентная |
|
Валентная |
|
|
|
зона |
|
зона |
|
а |
|
б |
|
в |
|
|
|
Рис. 1.3 |
|
|
Энергетическая диаграмма диэлектриков похожа на диаграмму полупроводников (рис. 1.34,в). Отличие состоит в большем значении ширины запрещенной зоны в диэлектриках Eg ≥ 3K4 эВ. Это значит, что
при одной и той же температуре число свободных носителей в диэлектриках еще меньше чем в полупроводниках.
Различие в электропроводности полупроводников и металлов качественное, а полупроводников и диэлектриков – количественное.
Структура кристаллической решетки кремния (Si) приведена на рис. 1.35. Взаимодействие четырехвалентных атомов в решетке осуществляется с помощью достаточно прочных ковалентных
(парноэлектронных) связей, за счет валентных электронов. Внешняя электронная оболочка каждого атома достраивается за счет валентных электронов соседних атомов. При увеличении температуры некоторые связи могут разрываться. Электрон покидает связь, если получил достаточное количество энергии. В этом случае он уже принадлежит всему ансамблю атомов и может перемещаться от одного из них к другому. На зонной диаграмме
это соответствует переходу электрона из валентной зоны в зону проводимости.
В полупроводниках существует два типа подвижных носителей заряда. Электрон проводимости или электрон, находящийся в зоне
проводимости, – подвижный носитель отрицательного заряда.
Дырка или вакантное место в валентной зоне – носитель положительного заряда. После ухода электрона из валентной зоны у оставшихся там электронов появляется возможность перемещаться с подуровня на подуровень в пределах валентной зоны. Такое перемещение отрицательного электрона оказывается удобнее рассматривать как встречное ему перемещение положительного заряда – дырки.
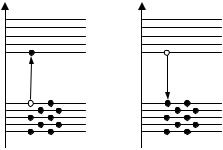
Генерация электронно-дырочной пары – процесс перехода электрона из валентной зоны в зону проводимости (рис. 1.36). Генерация сопровождается поглощением энергии величиной Eg или при повышении
температуры – термогенерация, или при поглощении кванта света –
фотогенерация.
|
|
|
Рекомбинация – процесс |
|||
|
|
|
исчезновения |
пары |
электрон- |
|
E |
E |
|
дырка, |
обратный |
генерации |
|
|
|
|
(рис. 1.36). |
В |
результате |
|
|
|
|
соударения |
с |
узлом |
|
|
Генерация |
Рекомбинация |
кристаллической решетки или |
|||
|
|
|
потери |
энергии |
электрон |
|
|
|
|
возвращается в валентную зону. |
|||
|
|
|
Сопровождается |
выделением |
||
|
Рис. 1.5 |
энергии |
или в виде фононов |
|||
|
(колебаний атомов), |
или в виде |
||||
|
|
|
фотонов |
|
(излучательная |
|
|
Собственными |
полупроводниками |
рекомбинация). |
|
||
|
называются |
полупроводники, в |
||||
узлах кристаллической решетки которых находятся атомы одного и того же элемента. Например, собственный германий (Ge), собственный кремний (Si).
Для собственных полупроводников число свободных электронов равно
числу дырок |
|
n = p = ni , |
(1.4.3) |
где n – концентрация свободных электронов (negative); p –концентрация дырок (positive); ni – параметр полупроводника, называемый собственная концентрация носителей. На значение ni влияет ширина запрещенной зоны полупроводника, чем выше значение Eg , тем меньше ni , и температура. С ростом температуры ni растет. В табл. 1.3 приведены
значения этих параметров для используемых при изготовлении электронных приборов полупроводников.
Процессы генерации и рекомбинации непрерывно происходят в полупроводнике, причем в некоторый фиксированный момент времени при определенной температуре T ≠ 0 K в собственном полупроводнике число
свободных электронов будет определяться значением ni .
Из (1.4.3) следует, что произведение концентрации электронов на концентрацию дырок для собственного полупроводника есть постоянная величина
n p = n2 |
= const . |
(1.4.4) |
i |
|
|
Собственные полупроводники обладают плохой электропроводностью, ввиду невысокой концентрации подвижных носителей заряда, которая значительно ниже, чем у проводников.
Таблица 1.3 Ширина запрещенной зоны и собственная концентрация носителей
различных полупроводников при T = 300 K
Полупроводник |
Ширина запрещенной |
Собственная концентрация |
|
зоны Eg , эВ |
носителей ni , см−3 |
Ge |
0,67 |
2,4 1013 |
Si |
1,12 |
1,45 1010 |
GaAs |
1,42 |
9,0 106 |
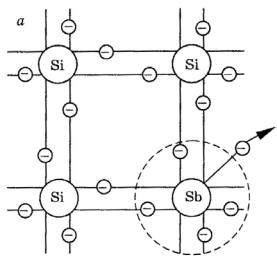
Примесными полупроводниками называются полупроводники, в
некоторых узлах кристаллической решетки которых находятся атомы, отличные от атомов основного вещества. Причем валентность примесных атомов должна быть отличной.
Если валентность атомов примеси выше валентности основных атомов, то такая примесь называется донорной примесью, а сам полупроводник
|
|
|
|
|
донорным |
полупроводником |
или |
|||
|
|
|
|
|
полупроводником |
|
n-типа. |
На |
||
|
|
|
|
|
рис. 1.37 представлена структура |
|||||
|
|
|
|
|
кристаллической решетки |
донорного |
||||
|
|
|
|
|
||||||
|
|
|
|
|
полупроводника |
|
на |
основе |
||
|
|
|
|
|
четырехвалентного |
Si, с |
примесью |
|||
|
|
|
|
|
атомов пятивалентной сурьмы (Sb). |
|||||
|
|
|
|
|
Четыре из пяти валентных электронов |
|||||
|
|
|
атома |
сурьмы |
|
|
оказались |
|||
|
|
ион |
|
|
|
|||||
|
|
|
|
задействованными |
в |
ковалентных |
||||
|
|
|
+ |
|||||||
|
|
|
|
|
связях с четырьмя атомами Si. Пятый |
|||||
|
|
|
|
|
||||||
|
|
|
|
|
электрон |
оказывается |
слабее |
|||
|
|
|
|
|
связанным |
с атомом |
Sb |
и для |
его |
|
высвобождения необходимо значение энергии меньше чем для разрыва ковалентной связи. Таким образом атомы примеси являются
поставщиками (донорами) свободных (подвижных) электронов. Атом примеси, отдавший один электрон, превращается в неподвижный положительно заряженный ион.

На зонной энергетической диаграмме донорного полупроводника данная ситуация моделируется дополнительным донорным уровнем (ДУ) с энергией Ed , который располагается в запрещенной зоне вблизи дна зоны
|
|
|
|
|
проводимости |
(рис. 1.38). Причем при T = 0 K ДУ |
||
|
|
|
|
|
заполнен. Уровень Ферми в донорном полупроводнике |
|||
|
|
E |
|
|
расположен между ДУ и дном зоны проводимости. |
|||
|
|
|
|
|
При T = 0 K |
в зоне |
проводимости |
отсутствуют |
|
Ec |
|
|
|||||
|
|
E f |
электроны и электропроводность отсутствует. Чтобы |
|||||
|
Ed |
|
||||||
|
|
|
попасть в зону проводимости, электронам на ДУ |
|||||
|
|
|
|
|||||
|
|
|
|
|
необходимо получить гораздо меньше энергии, чем |
|||
|
Ev |
|
|
|||||
|
|
|
электронам в валентной зоне. Эта энергия – энергия |
|||||
|
|
|
|
|||||
|
|
|
|
|
ионизации |
донорной |
примеси |
∆Ed = Ec − Ed . |
Поэтому такие переходы электронов с ДУ происходят при меньших температурах, чем переходы из валентной зоны. При ионизации донорной примеси появляется электрон проводимости, но при этом не
образуется вакантного места в валентной зоне (дырки). Таким образом, увеличивая концентрацию донорной примеси ND , можно увеличивать
концентрацию свободных электронов в донорном полупроводнике nn , не изменяя при этом концентрацию дырок pn . Если концентрация атомов
примеси будет значительно выше концентрации носителей в собственном полупроводнике ND >> ni , то можно считать, что электропроводность
обеспечивается только электронами, что и отражает название – полупроводник n-типа. Электроны в донорном полупроводнике являются основными носителями заряда, а дырки – неосновными. Для донорного полупроводника справедливо равенство подобное (1.4.4)
n |
p |
n |
= n2 . |
(1.4.5) |
n |
|
i |
|
Пользуясь (1.4.5) оценим концентрацию дырок, если концентрация атомов примеси много выше концентрации носителей в собственном
полупроводнике |
ND >> ni . |
Валентность примеси |
на единицу выше |
|||||
валентности атомов основного вещества. |
|
|||||||
Поскольку ND >> ni , то nn = ND + ni ≈ ND . |
(1.4.6) |
|||||||
Тогда p |
n |
= n2 |
n |
= n2 N |
D |
<n . |
(1.4.7) |
|
|
|
i |
n |
i |
i |
|
||
Из (1.4.7) видно, что концентрация дырок в полупроводнике n-типа уменьшается по сравнению с собственным полупроводником.
Если валентность атомов примеси ниже валентности основных атомов, то такая примесь называется акцепторной примесью, а сам полупроводник
акцепторным полупроводником или полупроводником p-типа. На рис. 1.39
представлена структура кристаллической решетки акцепторного полупроводника на основе четырехвалентного Si, с примесью атомов

|
трехвалентного |
индия |
(In). |
Три |
||
|
валентных |
электрона |
атома |
индия |
||
дырка |
||||||
оказались |
задействованными |
в |
||||
|
||||||
|
||||||
|
ковалентных связях с четырьмя атомами |
|||||
|
Si. Одна из ковалентных связей |
|||||
|
оказывается неполной. Она легко |
|||||
|
достраивается за счет электронов, |
|||||
|
покинувших основные атомы. Наличие |
|||||
|
примеси |
приводит к |
образованию |
|||
|
дырки. Таким образом атомы примеси |
|||||
–ион захватывают свободные электроны, т.е.являются акцепторами. Атом примеси,
принявший один электрон, превращается в неподвижный отрицательно заряженный ион.
На зонной энергетической диаграмме акцепторного полупроводника данная ситуация моделируется дополнительным акцепторным уровнем (АУ) с энергией Ea , который располагается в запрещенной зоне вблизи
потолка валентной зоны (рис. 1.40). Причем при T = 0 K АУ свободен.
Уровень Ферми в акцепторном полупроводнике расположен между потолком валентной зоны и АУ. При T = 0 K в зоне проводимости отсутствуют
электроны, а в валентной зоне – дырки, и электропроводность отсутствует. Чтобы попасть на АУ, электронам валентной зоны необходимо получить гораздо меньше энергии, чем для их попадания в зону проводимости. Эта энергия – энергия ионизации акцепторной примеси ∆Ea = Ea − Ev .
E
Ec
Ea  E f Ev
E f Ev 
Поэтому такие переходы электронов на АУ происходят при меньших температурах, чем переходы в зону проводимости. При ионизации акцепторной примеси появляется дырка, но при этом не появляется электрон в зоне проводимости. Таким образом, увеличивая концентрацию акцепторной примеси N A ,
можно увеличивать концентрацию дырок в акцепторном полупроводнике pp , не изменяя при
этом в енм концентрацию электронов np . Если
Рис. 1.9 |
концентрация атомов примеси будет значительно |
|
выше концентрации носителей в собственном |
||
|
||
|
полупроводнике N A >> ni , то можно считать, что |
электропроводность обеспечивается только за счет дырок, что и отражает название – полупроводник p-типа. Дырки в акцепторном полупроводнике являются основными носителями заряда, а электроны – неосновными. Для акцепторного полупроводника справедливо равенство подобное (1.4.4)
p |
p |
n |
p |
= n2 . |
(1.4.6) |
|
|
i |
|

Откуда следует, что если N A >> ni , то pp = N A + ni ≈ N A , |
(1.4.7) |
||||||||
и тогда n |
p |
= n2 |
p |
p |
= n2 |
N |
A |
<n . |
(1.4.8) |
|
i |
|
i |
|
i |
|
|||
Из (1.4.8) видно, что концентрация электронов в полупроводнике p- типа уменьшается по сравнению с собственным полупроводником.
Образец примесного полупроводника обладает электрической нейтральностью, несмотря на то, что концентрация одних носителей заряда много больше других. Эта разница компенсируется ионами атомов примеси соответствующего знака.
В полупроводниках существует два механизма перемещения свободных носителей заряда.
Дрейфовый ток – направленное перемещение носителей заряда, обусловленное наличием электрического поля.
Плотность электронного дрейфового тока определяется выражением
Jn dr = −qnvn = qnµnE , |
vn = −µnE , |
(1.4.9) |
а плотность дырочного дрейфового тока |
|
|
Jp dr = qpvp = qpµpE , |
vp = µpE , |
(1.4.10) |
где q =1,6022 10−19 Кл – |
элементарный электрический |
заряд; n, p – |
концентрация электронов и дырок соответственно; vn , vp – средняя скорость дрейфа электронов и дырок; µn , µp – подвижность электронов и
дырок; E – напряженность электрического поля.
Подвижность носителей заряда есть коэффициент пропорциональности между средней скоростью дрейфа и напряженностью электрического поля. Физический смысл данного параметра следует из выражения
µ = v E . |
(1.4.11) |
Таким образом подвижность – средняя скорость носителей в электрическом поле с единичной напряженностью. Размерность подвижности
[µ]= |
[v] |
|
= |
м м |
= |
м2 |
. |
(1.4.12) |
[E] |
с В |
|
||||||
|
|
|
В с |
|
||||
Подвижность зависит от типа полупроводника, концентрации примеси, температуры, напряженности поля:
1.с ростом температуры подвижность уменьшается;
2.при значениях концентрации примеси больше 1015 K1016 см−3
подвижность начинает падать;
3.в слабых полях подвижность постоянна, при напряженности поля выше критической подвижность обратно пропорциональна напряженности;
4.подвижность электронов выше подвижности дырок.
Суммарная плотность дрейфового тока определяется выражением
