Выборочный частный коэффициент корреляции

Точечная оценка   определяется по формуле:

,

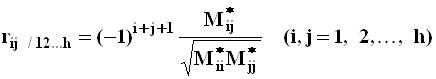здесь   - минор элемента   выборочной корреляционной матрицы  .

В случае трехмерной корреляционной модели для переменных   находятся три частных коэффициента корреляции:

;

;

.

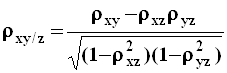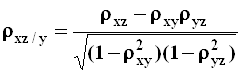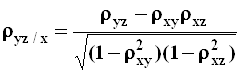 называется частным коэффициентом детерминации.

Величина   есть доля дисперсии переменной  , обусловленная вариацией   при фиксированных остальных рассматриваемых переменных.

Множественный коэффициент корреляции

Мерой тесноты линейной взаимосвязи между переменной   и совокупностью остальных переменных   служит множественный коэффициент корреляции:

,

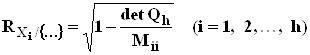Где   - определитель матрицы  ;

 - минор  -го элемента главной диагонали матрицы  .

Если  , то множественный коэффициент корреляции   совпадает с абсолютным значением парного коэффициента корреляции  , т.е.   есть обобщение  .

По величине множественного коэффициента корреляции делается вывод о тесноте, но не о направлении взаимосвязи.

Свойства множественного коэффициента корреляции

-  Численное значение множественного коэффициента корреляции заключено между нулем и единицей:

.

-  Если  , то переменная   связана с остальными рассматриваемыми случайными величинами   линейной функциональной зависимостью.

Например, для трехмерной корреляционной модели, если  , то точки   расположены в плоскости регрессии   на  .

-  Если  , то случайная величина   стохастически независима от других переменных, входящих в анализ.

В частности, если  , то одномерная случайная величина   и двумерная случайная величина  являются независимыми (в силу нормальности их совместного распределения).

-  Множественный коэффициент корреляции не уменьшается при введении в модель дополнительных признаков и не увеличивается при исключении отдельных признаков из модели.

-  По величине множественный коэффициент корреляции переменной   не меньше абсолютной величины частного коэффициента корреляции данной и любой другой переменной  :

.

Выборочный множественный коэффициент корреляции

В качестве точечной оценки   принимается

.

где   - минор  -го элемента главной диагонали выборочной корреляционной матрицы  .

В случае трехмерной корреляционной модели для переменных   вычисляются три множественных коэффициента корреляции:

;

;

.

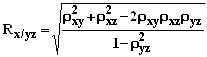 называется множественным коэффициентом детерминации.

Множественный коэффициент детерминации   показывает долю дисперсии исследуемой случайной величины  , обусловленную изменением остальных переменных  .

Коэффициент детерминации - квадрат линейного коэффициента корреляции, рассчитываемый для оценки качества подбора линейной функции.

№2

Парные коэффициенты корреляции. Для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретации аналогичны линейному коэффициенту корреляции в случае однофакторной связи.

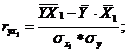
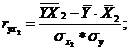
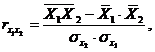
где   - среднее квадратическое отклонение факторного признака;

       - среднее квадратическое отклонение результативного признака.

Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели.

Для качественной оценки тесноты связи можно использовать следующую классификацию:

0.1- 0.3- слабая связь

0.3-0.5 – умеренная связь

0.5-0.7- заметная связь

0.7-0.9- тесная связь

0.9-0.99- весьма тесная

Для расчета частных коэффициентов корреляции мо­гут быть использованы парные коэффициенты корреляции.

Для случая зависимости Y от двух факторов можно вычислить 2 коэффициента частной корреляции:

   

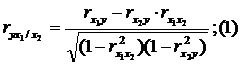
(2-ой фактор   фиксирован);

 

    

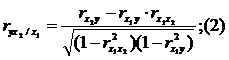
(1-ый фактор   фиксирован).

 

Это коэффициенты частной корреляции 1-ого порядка (порядок определяется числом факторов, влияние которых на результат устраняется).

Частные коэффициенты корреляции, рассчитанные по таким формулам изменяются от -1 до +1. Они используют­ся не только для ранжирования факторов модели по степени влияния на результат, но и также для отсева факторов. При малых значениях   нет смысла вводить в уравнение m-ый фактор, т.к. качество уравнения регрессии при его введении возрастет незначительно (т.е. теоретиче­ский коэффициент детерминации увеличится незначитель­но).

Совокупный коэффициент множественной корреляции или индекс множественной корреляцииопределяет тесноту совместного влияния факторов на результат:

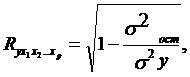
где   остаточная дисперсия;

или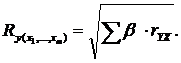 

. Он принимает значения от 0 до 1 (в отличие от парного коэффициента корреляции, который может прини­мать отрицательные значения, R используется без учета на­правления связи). Чем плотнее фактические значения   располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина  . Таким образом, при значении Rблизком к 1, урав­нение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат; при значении R близком к 0 уравнение регрессии плохо описывает фактиче­ские данные и факторы оказывают слабое воздействие на результат.

При трех переменных для двух факторного уравнения регрессии данная формула совокупного коэффициента множественной корреляции легко приводится к следующему виду:

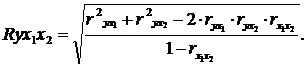
Чем R ближе к единице, тем совокупное влияние изучаемых показателей x1 и x2  на результативный фактор y больше (корреляционная связь более интенсивная).

 

Множественный (совокупный) коэффициент детерминации определим как квадрат множественного коэффициента корреляции. Показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии. Его значение - в пределах от нуля до единицы. Чем ближе множественный коэффициент детерминации к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов. 

№3

Корреляционный анализ является одним из методов статистического анализа взаимозависимости нескольких признаков.

Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке и определении на основе этой матрицы частных и множественных коэффициентов корреляции и детерминации.

Парный и частный коэффициенты корреляции характеризуют тесноту линейной зависимости между двумя переменными соответственно на фоне действия и при исключении влияния всех остальных показателей, входящих в модель. Они изменяются в пределах от -1 до +1, причем чем ближе коэффициент корреляции к 1, тем сильнее зависимость между переменными. Если коэффициент корреляции больше нуля, то связь положительная, а если меньше нуля — отрицательная.

Множественный коэффициент корреляции характеризует тесноту, линейной связи между одной переменной (результативной) и остальными, входящими в модель; он изменяется в пределах от 0 до 1.

Квадрат множественного коэффициента корреляции называется множественным коэффициентом детерминации. Он характеризует долю дисперсии одной переменной (результативной), обусловленной влиянием всех остальных переменных (аргументов), входящих в модель.

67. Проверка значимости частного и множественного коэффициентов корреляции.