
- •Экзаменационные вопросы по дисциплине «Теория вероятностей и математическая статистика»
- •Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.
- •Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии.
- •50. Доверительный интервал для дисперсии нормального распределения при известном и неизвестном математическом ожидании.
- •51. Доверительное оценивание вероятности (генеральной доли признака) – параметра биномиального распределения.
- •52. Понятие «статистическая гипотеза». Статистический критерий. Статистика критерия. Область отвержения гипотезы.
- •53. Ошибки первого и второго рода. Уровень значимости и мощность статистического критерия. Наиболее мощный критерий. Условия, определяющие критическую область наиболее мощного критерия.
- •54. Этапы процедуры проверки статистической гипотезы с помощью критерия заданного уровня значимости.
- •55. Проверка гипотезы о числовом значении математического ожидания (генеральной средней) нормального распределения.
- •56. Проверка гипотезы о числовом значении дисперсии нормального распределения.
- •57. Проверка гипотезы о числовом значении вероятности (генеральной доли признака) – параметра биноминального распределения.
- •58. Проверка гипотезы о равенстве математических ожиданий (генеральных средних) двух нормальных распределений.
- •59. Проверка гипотезы о равенстве дисперсий двух нормальных распределений.
- •60. Проверка гипотезы о равенстве вероятностей (генеральных долей признака) для двух биномиально распределённых генеральных совокупностей.
- •Предпосылки корреляционного анализа
- •Двумерная корреляционная модель
- •Уравнения линейной парной регрессии
- •Интервальная оценка коэффициента корреляции
- •Этапы определения ди(доверительного интервала) для коэффициента корреляции
- •Доверительные интервалы для коэффициентов регрессии
- •Частный коэффициент корреляции
- •Выборочный частный коэффициент корреляции
- •Множественный коэффициент корреляции
- •Свойства множественного коэффициента корреляции
- •Выборочный множественный коэффициент корреляции
- •Проверка значимости коэффициентов связи а) для частного коэффициента корреляции
- •Б) для множественного коэффициента корреляции
- •Уравнения регрессии для трехмерной корреляционной модели
Интервальная оценка коэффициента корреляции
корреляционная регрессия уравнение математический
При
построении доверительного интервала
для неизвестного коэффициента
корреляции
используется
специальная функция - ![]() -преобразование
Фишера (гиперболический арктангенс)
выборочного коэффициента корреляции r:
-преобразование
Фишера (гиперболический арктангенс)
выборочного коэффициента корреляции r:
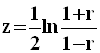 .
.
![]() -
возрастающая нечетная функция: z(-r)
= -z(r).
-
возрастающая нечетная функция: z(-r)
= -z(r).
Распределение
вероятностей значений ![]() приближается
(тем более точно, чем больше объем
выборки n)нормальным
распределением вероятностей
приближается
(тем более точно, чем больше объем
выборки n)нормальным
распределением вероятностей ![]() с
параметрами:
с
параметрами:
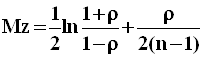 и
и 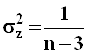 .
.
Статистика 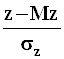 имеет
асимптотическое стандартное нормальное
распределение
имеет
асимптотическое стандартное нормальное
распределение ![]() .
.
Асимптотически
точный доверительный интервал
надежности ![]() для
нормированного отклонения z:
для
нормированного отклонения z:
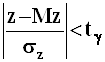 ,
,
где ![]() -
квантиль уровня
-
квантиль уровня ![]() распределения
,
т.е. корень уравнения
распределения
,
т.е. корень уравнения ![]() .
.
Доверительный
интервал для математического ожидания ![]() :
:
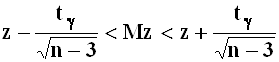 .
.
Величиной 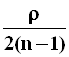 в
выражении
в
выражении ![]() можно
пренебречь, принимая во внимание, что
она при
можно
пренебречь, принимая во внимание, что
она при ![]() есть
бесконечно малая более высокого порядка
в сравнении с
есть
бесконечно малая более высокого порядка
в сравнении с 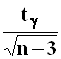 .
.
Доверительный
интервал для гиперболического арктангенса
коэффициента корреляции ![]() :
:
 .
.
Решение относительно данного двойного неравенства приводит к искомому доверительному интервалу для коэффициента корреляции:
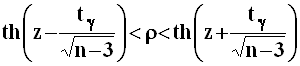 ,
,
с
границами, определяемыми как значения
гиперболического тангенса  для
значений
для
значений ![]() ,
равных соответственно
,
равных соответственно  и
и  .
.
Функция ![]() задает
преобразование, обратное
-преобразованию
Фишера. Следовательно,
задает
преобразование, обратное
-преобразованию
Фишера. Следовательно, ![]() .
.
Этапы определения ди(доверительного интервала) для коэффициента корреляции
- находится выборочный коэффициент корреляции r;
-
выполняется прямое преобразование
Фишера значения r: ![]() ;
;
-
выбирается квантиль ![]() ,
исходя из условия
,
исходя из условия ![]() ;
;
-
вычисляются значения  и
и 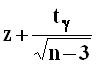 ;
;
- с помощью обратного преобразования Фишера находятся границы ДИ:
 и
и  .
.
Доверительные интервалы для коэффициентов регрессии
Их построение осуществляется в соответствии с общей схемой. При этом используются статистики:
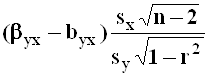 ;
; 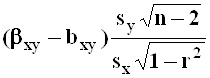 ,
,
имеющие
распределение Стьюдента с числом
степеней свободы, равном ![]() .
.
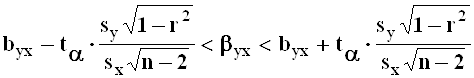 ;
;
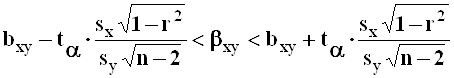 ,
,
где ![]() -
корень уравнения
-
корень уравнения ![]() .
.
66. Трехмерная корреляционная модель. Частные и множественные коэффициенты корреляции и детерминации, их свойства.
№1
Частный коэффициент корреляции
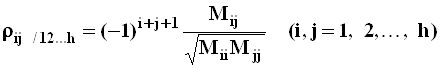 ,
,
где ![]() -
минор элемента
-
минор элемента ![]() матрицы
матрицы ![]() ,
т.е. определитель матрицы, получающейся
из корреляционной матрицы удалением
,
т.е. определитель матрицы, получающейся
из корреляционной матрицы удалением ![]() -ой
строки и
-ой
строки и ![]() -го
столбца.
-го
столбца.
Свойства частного коэффициента корреляции
![]() обладает
всеми свойствами парного коэффициента
корреляции
обладает
всеми свойствами парного коэффициента
корреляции ![]() ,
т.к. является коэффициентом корреляции
,
т.к. является коэффициентом корреляции ![]() для
их условного двумерного распределения.
В отличие от парного коэффициента
корреляции
,
на величине которого сказывается не
только влияние переменных
друг
на друга, но и воздействие
остальных
для
их условного двумерного распределения.
В отличие от парного коэффициента
корреляции
,
на величине которого сказывается не
только влияние переменных
друг
на друга, но и воздействие
остальных ![]() переменных,
частный коэффициент корреляции
позволяет
характеризовать тесноту связи между
признаками
в
«чистом» виде, исключая при анализе
зависимости влияние других переменных.
Если парный коэффициент корреляции
больше
соответствующего частного коэффициента
,
то можно заключить, что остальные
рассматриваемые переменные усиливают
взаимосвязь между изучаемыми величинами
переменных,
частный коэффициент корреляции
позволяет
характеризовать тесноту связи между
признаками
в
«чистом» виде, исключая при анализе
зависимости влияние других переменных.
Если парный коэффициент корреляции
больше
соответствующего частного коэффициента
,
то можно заключить, что остальные
рассматриваемые переменные усиливают
взаимосвязь между изучаемыми величинами ![]() .
Уменьшение значения парного коэффициента
корреляции, в сравнении с отвечающим
ему частным коэффициентом корреляции,
свидетельствует об ослаблении связи
между исследуемыми величинами
в
результате воздействия других переменных.
.
Уменьшение значения парного коэффициента
корреляции, в сравнении с отвечающим
ему частным коэффициентом корреляции,
свидетельствует об ослаблении связи
между исследуемыми величинами
в
результате воздействия других переменных.
