
- •Оглавление
- •Введение
- •Раздел 1 применение методов интегрирования функции в задачах лазерных технологий Теоретические сведения
- •Неопределенный интеграл
- •Определенный интеграл
- •Несобственные интегралы
- •Интегрирование функций нескольких переменных
- •Интегрирование в других системах координат
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 2 применение методов исследования функции на экстремум в задачах лазерных технологий Теоретические сведения
- •Возрастающая и убывающая функции
- •Экстремумы функции
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 3
- •Применение методов исследования интеграла вероятностей в задачах лазерных технологий
- •Теоретические сведения
- •Интеграл вероятностей и дополнительный интеграл вероятностей
- •2. Кратные интегралы вероятностей
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 4
- •Применение методов исследования линейных дифференциальных уравнений в задачах
- •Лазерных технологий
- •Теоретические сведения
- •Однородные и неоднородные уравнения
- •Общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
- •3. Частное решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной правой частью
- •Задача 5
- •Решение
- •Задача 6
- •Уравнение теплопроводности. Закон Фурье
- •2. Длина теплопроводности
- •3. Частные случаи уравнения теплопроводности
- •4. Граничные и начальные условия
- •5. Источник
- •6. Уравнение теплопроводности в других системах координат
- •7. Уравнение теплопроводности при движущемся источнике тепла
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 5
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 6 применение методов исследования преобразования лапласа в задачах лазерных технологий Теоретические сведения
- •1. Преобразование Лапласа и обратное преобразование Лапласа
- •2. Основные свойства преобразования Лапласа
- •Примеры решения задач Задача 1
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 7
- •Применение метода источников
- •В задачах лазерных технологий
- •Теоретические сведения
- •Сущность метода и элементарные решения
- •2. Основные методики определения совокупности элементарных источников
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задача 4
- •Решение
- •Задачи для самостоятельного решения
- •Список рекомендуемой литературы
2. Кратные интегралы вероятностей
Кратными интегралами вероятностей называются функции, определяемые выражениями:
 ,
,
 ,
(3.10)
,
(3.10)
………………………………………
 .
.
По
определению принимается:
![]() ,
,
 .
.
Графики кратных интегралов вероятностей выглядят следующим образом:
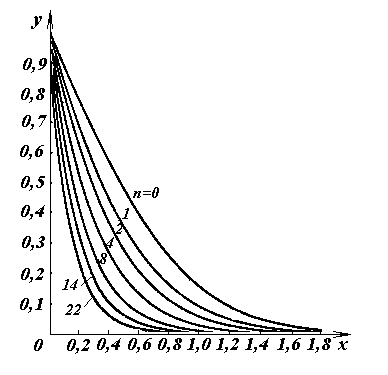
Рис.
3.2. Кратные интегралы вероятностей
![]() .
.
Значения в нуле:
 ,
(3.11)
,
(3.11)
где
![]() –
гамма-функция. В частности,
–
гамма-функция. В частности,
![]() ,
,
![]() .
.
Значения
на бесконечности:
![]() .
.
Рекуррентные
соотношения позволяют выразить кратные
интегралы
![]() друг через друга, понижая значение п.
Для п
=1 и п=2:
друг через друга, понижая значение п.
Для п
=1 и п=2:
 ,
(3.12)
,
(3.12)
 .
(3.13)
.
(3.13)
Для произвольных значений п рекуррентные соотношения можно найти в справочнике [8].
Производные:
![]() ,
,
![]() (3.14)
(3.14)
Интегралы вероятностей присутствуют во многих выражениях, являющихся решениями теплофизических задач нагревания вещества лазерным излучением, например в следующих.
1. На
поверхность металла или другого сильно
поглощающего материала падает пучок
лазерного излучения. Радиус облученной
области
достаточно
велик:
![]() (где
а
–
температуропроводность материала,
–
время
воздействия излучения). Плотность
мощности падающего
излучения
(где
а
–
температуропроводность материала,
–
время
воздействия излучения). Плотность
мощности падающего
излучения
![]() постоянна во времени и
по
сечению пучка. При этом
распределение температуры по глубине
материала имеет вид:
постоянна во времени и
по
сечению пучка. При этом
распределение температуры по глубине
материала имеет вид:
 ,
(3.15)
,
(3.15)
где
А
–
поглощательная
способность материала, k
–
его теплопроводность,
t
– время от начала воздействия, ось у
направлена
от поверхности вглубь материала. Здесь
и везде
дальше температуру отсчитываем от
начального значения. Заметим, что
представление о достаточно большом
размере облученной области (
)
имеет относительный характер, в частности,
для импульсов наносекундной длительности
размер облученной области
![]() мкм
является достаточно большим.
мкм
является достаточно большим.
2. Та же ситуация, что и в примере 1, но радиус облученной области может быть любой, в том числе достаточно малый. Температура на поверхности в центре облученной области:
 .
(3.16)
.
(3.16)
3. Пучок лазерного
излучения падает на поверхность тонкой
металлической пленки, находящейся на
прозрачной диэлектрической подложке.
Плотность мощности излучения постоянна
во времени и по сечению пучка. Облученная
область имеет форму круга, причем его
радиус
.
Время воздействия излучения
![]() с.
Распределение температуры в пленке
имеет вид:
с.
Распределение температуры в пленке
имеет вид:
 .
(3.17)
.
(3.17)
где r – радиус в полярной системе координат на поверхности пленки, полюс которой совпадает с центром облученной области, с – теплоемкость материала пленки, h – толщина пленки, – плотность пленки.
4.
Лазерное хирургическое лечение
злокачественной опухоли производится
путем введения зонда в ее центр, через
который с помощью
оптического волокна подается лазерное
излучение. Конец зонда излучает
световую энергию равномерно во все
стороны. Распределение
температуры в биоткани имеет также
сферическую симметрию и определяется
зависимостью (исключая область
![]() ):
):
 .
(3.18)
.
(3.18)
где P – мощность излучения, r – радиус в сферической системе координат, центр которой совпадает с центром симметрии распределения интенсивности излучения.
