
- •Оглавление
- •Введение
- •Раздел 1 применение методов интегрирования функции в задачах лазерных технологий Теоретические сведения
- •Неопределенный интеграл
- •Определенный интеграл
- •Несобственные интегралы
- •Интегрирование функций нескольких переменных
- •Интегрирование в других системах координат
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 2 применение методов исследования функции на экстремум в задачах лазерных технологий Теоретические сведения
- •Возрастающая и убывающая функции
- •Экстремумы функции
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 3
- •Применение методов исследования интеграла вероятностей в задачах лазерных технологий
- •Теоретические сведения
- •Интеграл вероятностей и дополнительный интеграл вероятностей
- •2. Кратные интегралы вероятностей
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 4
- •Применение методов исследования линейных дифференциальных уравнений в задачах
- •Лазерных технологий
- •Теоретические сведения
- •Однородные и неоднородные уравнения
- •Общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
- •3. Частное решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной правой частью
- •Задача 5
- •Решение
- •Задача 6
- •Уравнение теплопроводности. Закон Фурье
- •2. Длина теплопроводности
- •3. Частные случаи уравнения теплопроводности
- •4. Граничные и начальные условия
- •5. Источник
- •6. Уравнение теплопроводности в других системах координат
- •7. Уравнение теплопроводности при движущемся источнике тепла
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 5
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 6 применение методов исследования преобразования лапласа в задачах лазерных технологий Теоретические сведения
- •1. Преобразование Лапласа и обратное преобразование Лапласа
- •2. Основные свойства преобразования Лапласа
- •Примеры решения задач Задача 1
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 7
- •Применение метода источников
- •В задачах лазерных технологий
- •Теоретические сведения
- •Сущность метода и элементарные решения
- •2. Основные методики определения совокупности элементарных источников
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задача 4
- •Решение
- •Задачи для самостоятельного решения
- •Список рекомендуемой литературы
Раздел 2 применение методов исследования функции на экстремум в задачах лазерных технологий Теоретические сведения
Возрастающая и убывающая функции
Функция
называется неубывающей на промежутке
![]() ,
если для любых величин
,
если для любых величин
![]()
![]() ,
принадлежащих этому промежутку,
выполняется условие:
,
принадлежащих этому промежутку,
выполняется условие:
![]() .
.
Функция называется невозрастающей на промежутке , если для любых величин , принадлежащих этому промежутку, выполняется условие:
![]() .
.
Если неравенства строгие (< или >), функция называется строго возрастающей или строго убывающей.
Неубывающая, невозрастающая, убывающая и возрастающая функции называются монотонными.
Все дальнейшие рассуждения будут относиться к функциям, дифференцируемым на некотором интересующем нас промежутке.
Для того, чтобы узнать, возрастающая функция или убывающая, нужно найти ее производную и определить ее знак. Если функция на промежутке такова, что:
![]() ,
то
–
неубывающая на
.
,
то
–
неубывающая на
.
![]() ,
то
–
строго возрастающая на
.
,
то
–
строго возрастающая на
.
![]() ,
то
–
невозрастающая на
.
,
то
–
невозрастающая на
.
![]() ,
то
–
строго убывающая на
.
,
то
–
строго убывающая на
.
Связь
между знаком производной и направлением
изменения функции геометрически
очевидна, если вспомнить, что производная
представляет собой тангенс угла наклона
касательной к графику функции. Если
касательная направлена вверх (тангенс
угла наклона положителен), то и кривая
направлена вверх (функция возрастает).
Если касательная направлена вниз
(тангенс угла наклона отрицателен), то
и кривая направлена вниз (функция
убывает) (см. рис. 2.1.). Однако при этом в
отдельных точках производная может
быть равна нулю (т.е. касательная
горизонтальна). Например, функция
![]() возрастающая, но в точке х
= 0 функция становится равной нулю (см.
рис.2.2).
возрастающая, но в точке х
= 0 функция становится равной нулю (см.
рис.2.2).
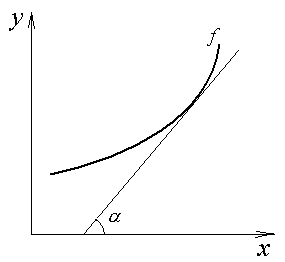
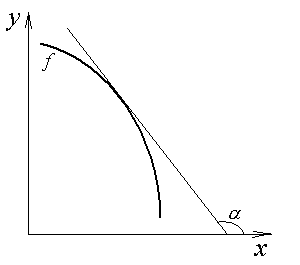
а б
Рис.2.1. Возрастающая (а) и убывающая (б) функции.

Рис.2.2. Функция .
Экстремумы функции
Пусть
функция
определена на некотором интервале
.
Говорят, что
имеет максимум в точке![]() ,
принадлежащей этому интервалу, если ее
значение во всех остальных точках
некоторой окрестности точки
,
также принадлежащей интервалу
,
меньше или равно значению функции в
точке
:
,
принадлежащей этому интервалу, если ее
значение во всех остальных точках
некоторой окрестности точки
,
также принадлежащей интервалу
,
меньше или равно значению функции в
точке
:
![]() .
.
Если
![]() ,
говорят, что функция имеет минимум в
точке
.
,
говорят, что функция имеет минимум в
точке
.
Если
![]() ,
,
![]() ,
то говорят, что функция имеет строгий
минимум и максимум в точке
соответственно.
,
то говорят, что функция имеет строгий
минимум и максимум в точке
соответственно.
Максимумы и минимумы функции называются также ее экстремумами.
Экстремум функции возможен в так называемых критических точках, т.е. в точках, в которых производная функции равна нулю, обращается в бесконечность или не существует.
Приведем некоторые примеры (см. рис.2.З):
а)
Функция
![]() .
В точке х
= 0
.
В точке х
= 0
![]() = 0.
= 0.
б)
Функция
![]() .
При
.
При
![]()
![]() .
.
в)
Функция
![]() .
.
![]() ,
,
![]() ,
,
![]() не существует.
не существует.
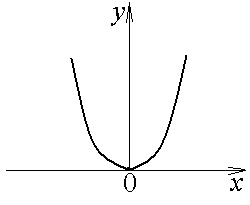
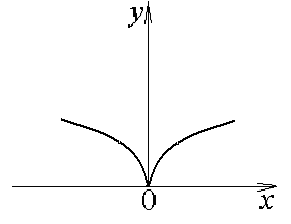
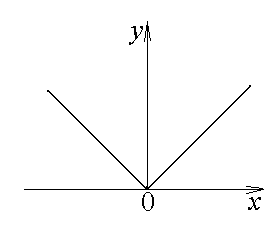
а б в
Рис. 2.3. Графики функций а) , б) , в) .
Заметим, что критическая точка не всегда является точкой экстремума. Например, производная функции в точке х = 0 равна нулю, однако экстремума в этой точке нет (см. рис.2.2).
Для того, чтобы определить, является ли критическая точка точкой экстремума и какой это будет экстремум (максимум или минимум), нужно определить, меняет ли знак производная функции, проходя через критическую точку. Пусть на экстремум проверяется точка . Возможны следующие ситуации:
![]()
![]()
1. ---- – максимум.
2. ---- – минимум.
3. ---- – экстремума нет (функция возрастает).
4. ---- – экстремума нет (функция убывает).
Существует
еще один способ определения экстремума,
который пригоден лишь для тех критических
точек, в которых производная функции
равна нулю. Если в такой точке
функция имеет вторую производную
![]() и она отрицательна, то в точке
функция имеет максимум, если положительна
–
минимум.
и она отрицательна, то в точке
функция имеет максимум, если положительна
–
минимум.
Таким образом, процедура исследования функции на экстремум заключается в следующем:
1.
Определяем
![]() .
.
2. Находим критические точки.
За. Определяем знак по обе стороны вблизи критической точки и определяем наличие или отсутствие максимума и минимума в точке.
или
3б.
Если критические точки
такие,
что
=
0 при х
=
,
находим
![]() и определяем по ее знаку наличие минимума
или максимума в точке.
и определяем по ее знаку наличие минимума
или максимума в точке.
