- •Оглавление
- •Введение
- •Раздел 1 применение методов интегрирования функции в задачах лазерных технологий Теоретические сведения
- •Неопределенный интеграл
- •Определенный интеграл
- •Несобственные интегралы
- •Интегрирование функций нескольких переменных
- •Интегрирование в других системах координат
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 2 применение методов исследования функции на экстремум в задачах лазерных технологий Теоретические сведения
- •Возрастающая и убывающая функции
- •Экстремумы функции
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 3
- •Применение методов исследования интеграла вероятностей в задачах лазерных технологий
- •Теоретические сведения
- •Интеграл вероятностей и дополнительный интеграл вероятностей
- •2. Кратные интегралы вероятностей
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 4
- •Применение методов исследования линейных дифференциальных уравнений в задачах
- •Лазерных технологий
- •Теоретические сведения
- •Однородные и неоднородные уравнения
- •Общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
- •3. Частное решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной правой частью
- •Задача 5
- •Решение
- •Задача 6
- •Уравнение теплопроводности. Закон Фурье
- •2. Длина теплопроводности
- •3. Частные случаи уравнения теплопроводности
- •4. Граничные и начальные условия
- •5. Источник
- •6. Уравнение теплопроводности в других системах координат
- •7. Уравнение теплопроводности при движущемся источнике тепла
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 5
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 6 применение методов исследования преобразования лапласа в задачах лазерных технологий Теоретические сведения
- •1. Преобразование Лапласа и обратное преобразование Лапласа
- •2. Основные свойства преобразования Лапласа
- •Примеры решения задач Задача 1
- •Решение
- •Задачи для самостоятельного решения
- •Раздел 7
- •Применение метода источников
- •В задачах лазерных технологий
- •Теоретические сведения
- •Сущность метода и элементарные решения
- •2. Основные методики определения совокупности элементарных источников
- •Примеры решения задач Задача 1
- •Решение
- •Задача 2
- •Решение
- •Задача 3
- •Решение
- •Задача 4
- •Решение
- •Задачи для самостоятельного решения
- •Список рекомендуемой литературы
Интегрирование в других системах координат
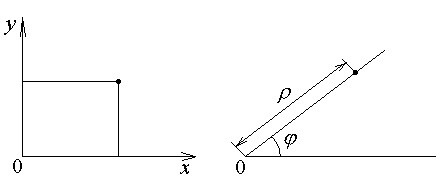
Рассмотрим интегрирование в полярной системе координат. Полярная система координат задается полюсом, полярной осью и единицей масштаба.
а б
Рис. 1.4. Декартовая (а) и полярная (б) системы координат.
Координаты точки в полярной и декартовой системе координат связаны соотношениями:
![]() .
(1.14)
.
(1.14)
При
переводе интеграла из одной системы
координат в другую при
переходе от дифференциалов
![]() и
и
![]() к
новым дифференциалам
к
новым дифференциалам
![]() образуется сомножитель, который
называется якобианом. Для полярной
системы координат:
образуется сомножитель, который
называется якобианом. Для полярной
системы координат:
![]() .
(1.15)
.
(1.15)
Примеры решения задач Задача 1
Определить
энергию импульса лазерного излучения,
если мощность
его зависит от времени следующим образом:
![]()
![]() Вт,
Вт,
![]() 1/с,
длительность импульса
1/с,
длительность импульса
![]() с.
с.
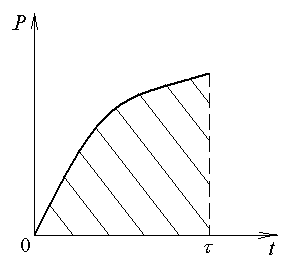
Рис. 1.5. К решению задачи 1.
Решение
Энергия
импульса определяется как интеграл от
мощности Р
по
времени
t
(время
действия импульса
![]() ):
):
 .
.
Делаем замену переменной и пересчет пределов интегрирования:
![]()
![]() ,
,
![]() .
.
Используя значения U и dU, получим:
 .
.
Из
таблицы интегралов находим:
![]() .
.
![]()
![]()
![]() .
.
Вычислим энергию импульса, подставив в полученную формулу числовые значения. Получим Е = 0,4 Дж.
Задача 2
Определить
зависимость от времени температуры
тонкой пластины,
нагреваемой излучением равномерно по
объему, если мощность излучения
зависит от времени
![]() ,
коэффициент отражения пластины R,
а
начальная температура пластины
,
коэффициент отражения пластины R,
а
начальная температура пластины![]() .
.
Решение
Известно,
что увеличение температуры тела на
величину
![]() требует
затраты энергии
требует
затраты энергии
![]() ,
где
m
–
масса тела, с
–
его
теплоемкость.
,
где
m
–
масса тела, с
–
его
теплоемкость.
Перейдем
к бесконечно малым приращениям:![]() .
Отсюда
.
Отсюда
![]() .
Энергия и мощность связаны соотношением:
.
Энергия и мощность связаны соотношением:
![]() ,
где
,
где
![]() –
поглощенная мощность. Таким образом:
–
поглощенная мощность. Таким образом:
![]()
![]() .
.
Температуру
пленки находим, интегрируя последнее
выражение.
 .
Отсюда
.
Отсюда
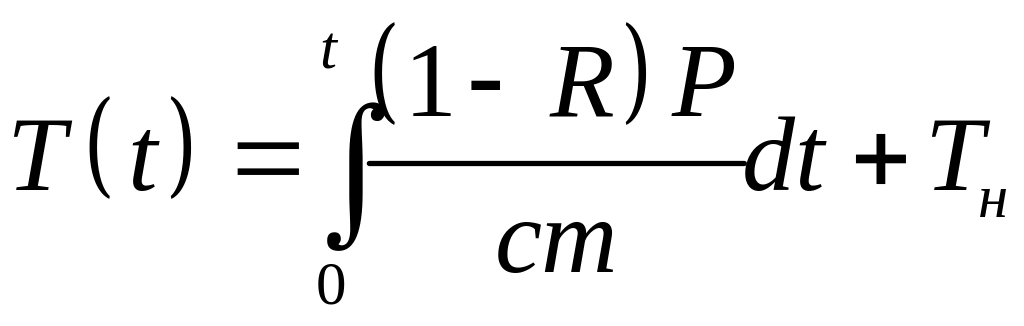 .
Если
.
Если
![]() ,
то:
,
то:
![]() .
.
Задача 3
Определить
мощность излучения, падающего на
поверхность, если облученная
область имеет вид круга радиуса
![]() и
плотность
мощности излучения
в ней распределена по закону
и
плотность
мощности излучения
в ней распределена по закону
![]() ,
где
,
где![]() ,
,
![]() –
полярные
координаты в плоскости поверхности.
–
полярные
координаты в плоскости поверхности.
Решение
Мощность излучения, падающего на поверхность, есть интеграл плотности мощности излучения по данной поверхности (в данном случае – по кругу), т.е.
 .
.
Для гауссова распределения плотности мощности излучения
![]()
 .
.
Проведем
замену переменной
![]() и пересчет пределов интегрирования.
Получим:
и пересчет пределов интегрирования.
Получим:

Задачи для самостоятельного решения
Определить
энергию импульса лазерного излучения
длительностью
,
если мощность его зависит от времени
следующим образом
![]() (1.1-1.5):
(1.1-1.5):
1.1.
![]() 1.4.
1.4.
![]()
1.2.
![]() 1.5.
1.5.
![]()
1.3.

Определить
зависимость от времени средней температуры
пластины,
нагреваемой импульсом лазерного
излучения, если коэффициент
отражения поверхности
![]() ,
а
мощность излучения, падающего на
пластину,
изменяется во времени по закону
(1.6
-1.10):
,
а
мощность излучения, падающего на
пластину,
изменяется во времени по закону
(1.6
-1.10):
1.6. ![]() 1.9.
1.9.
![]()
1.7. ![]() 1.10.
1.10.
![]()
1.8. 
Определить, используя полярную систему координат, мощность излучения, падающего на поверхность, если облученная область имеет вид круга радиуса и плотность мощности в ней распределена по закону (1.11-1.15):
1.11.
![]() .
1.14.
.
1.14.

1.12.
 1.15.
1.15.

1.13.