Примеры решения задач Задача 1

Производится облучение полубесконечного сильно поглощающего тела. Плотность мощности излучения q постоянна на поверхности тела и во времени. Определить распределение температуры по толщине тела в момент окончания импульса излучения.

Решение

Проанализируем условие задачи:

1) ;

2) источник продолжительного действия;

3) распределение источников по поверхности равномерное;

4) ;

5) так как тело занимает полупространство, будем рассматривать задачу нагревания всего пространства источником плотности мощности . ( - плотность мощности излучения, R – коэффициент отражения).

Итак, температура при действии точечного мгновенного единичного источника:

.

Размерность числителя: [Дж/м²].

При действии источника с плотностью энергии :

.

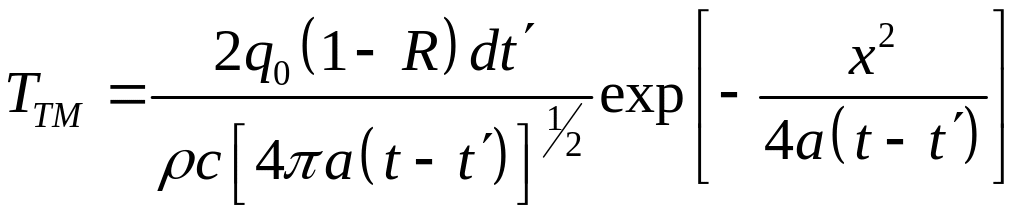Интегрируя по времени, определяем температуру при действии точечного продолжительного источника с плотностью мощности :

.

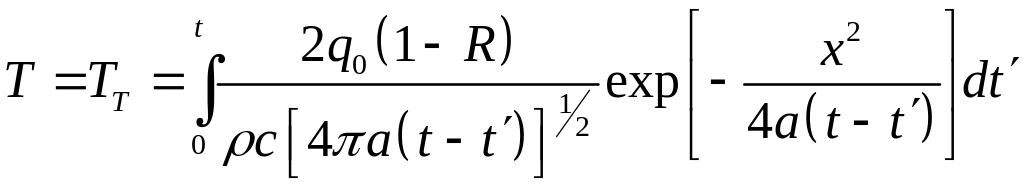Вычисляем интеграл, делая замену переменной: .

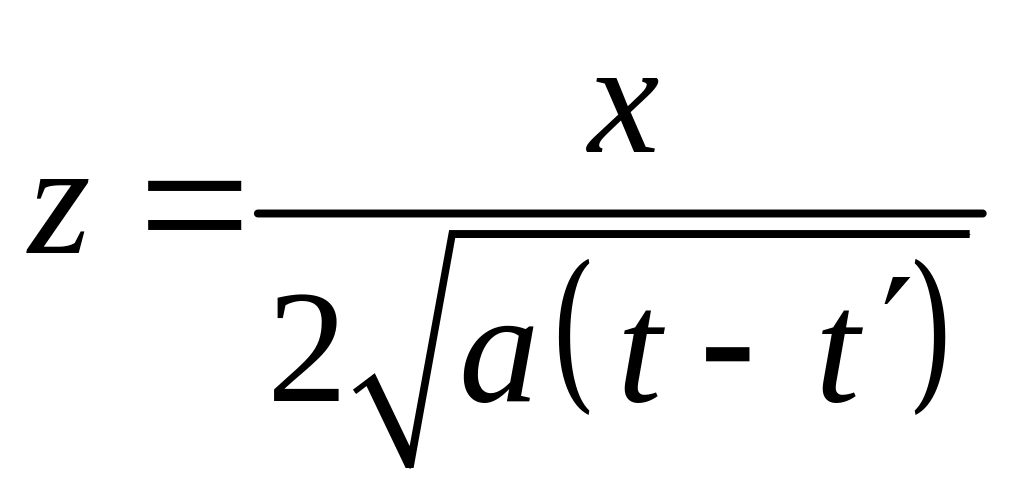Находим дифференциал новой переменной :

Отсюда:

Таким образом,

Вычислим последний интеграл. Берем интеграл по частям, обозначив , .

Получим:

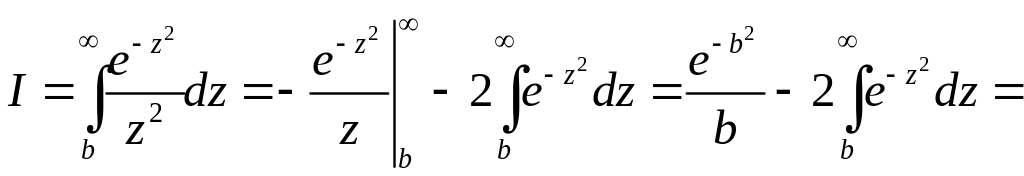
Таким образом, температура на глубине x в момент времени t с начала облучения:

где – теплопроводность тела.

В момент окончания импульса излучения :

Задача 2

Производится облучение тонкой поглощающей пленки. Облученная область представляет собой половину ее поверхности ( ). Плотность мощности излучения распределена равномерно по облученной области и во времени. Определить распределение температуры по поверхности пленки во время действия импульса излучения.

Решение

Проанализируем условия задачи:

1) п= 1;

2) источник продолжительного действия;

3) распределение источников – равномерное, ;

4) .

Температура одномерного тела при действии на него точечного мгновенного единичного источника:

.

Рис. 7.4. К задаче 2.

Размерность числителя: [Дж/м²].

При действии источника с энергией

.

Интегрируя по и , определим зависимость во время действия излучения:

.

Интегрирование по с заменой переменной дает (см. предыдущую задачу):

,

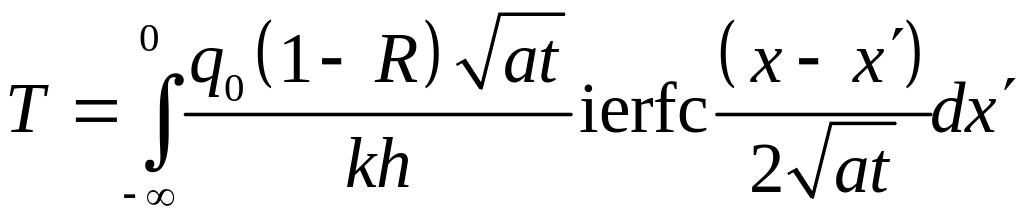где – теплопроводность пленки.

Интегрирование по с заменой переменной дает:

Задача 3

Производится облучение тонкой поглощающей пленки толщиной h. Облученная область – квадрант ( , ). Плотность мощности излучения распределена равномерно по облученной области и во времени. Определить температуру в точке ( , ) в момент времени .

Решение

Проанализируем условия задачи:

1) ;

2) источник продолжительного действия;

3) распределение источника – равномерное в облученной области ( , );

4) .

Температура в точке ( , ) при действии точечного мгновенного единичного источника:

,

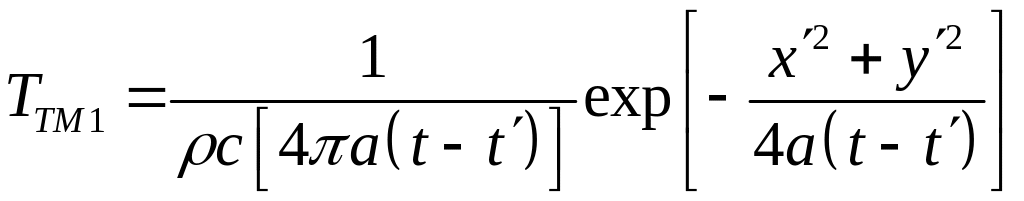Размерность числителя: [Дж/м].

При действии источника с энергией :

.

Интегрируя по х', у', t', определим при :

.

Интегрируем каждый из двух интегралов в квадратных скобках, делая замену переменной , :

.