
- •Іі Розвиток уявлень про атом
- •1. Ідея атомізма. Дискретність речовини. Дискретність електричного заряду
- •2. Спектри випромінювання тіл. Лінійчасті спектри атомів. Серіальна формула Бальмера
- •1) Тверді тіла і рідини випромінюють суцільний спектр.
- •2) Спектри молекул – полосаті (окремі полоси).
- •3) Спектри атомів в газоподібному стані мають чітко окреслені лінії – їх називають лінійчастими.
- •3. Модель атома Томсона
- •4. Дослід Резерфорда. Ядерна модель атома
- •5. Протиріччя ядерної моделі атома Резерфорда з законами класичної фізики.
- •6. Постулати Бора. Правило квантування Бора.
- •1. Електрони в атомі рухаються тільки по дозволеним стаціонарним орбітам, не випромінюючи і не поглинаючи енергію.
- •7. Напівквантова модель атома Бора
- •8. Дослід Франка і Герца
6. Постулати Бора. Правило квантування Бора.
Вихід із цього кризового стану був знайдений датським фізиком Нільсом Бором у 1913р., який працював у той час в Манчестерському університеті у Е. Резерфорда. Бор застосував квантову гіпотезу М. Планка до моделі атома Резерфорда, сформулювавши свої постулати:
1. Електрони в атомі рухаються тільки по дозволеним стаціонарним орбітам, не випромінюючи і не поглинаючи енергію.
2.
Випромінювання або поглинання світла
атомом відбувається при переході
електрона з однієї стаціонарної орбіти
на іншу, згідно з законом збереження
енергії:
 ( - умова частот Бора).
( - умова частот Бора).
Умови для стаціонарних орбіт Бор знайшов, виходячи з гіпотези Планка, згідно якої здійснюються тільки ті стани гармонічного осцилятора, енергія яких рівна:

Тут
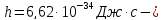 стала Планка,
стала Планка,
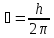 = 1,05
= 1,05 .
.
Звідси випливає, що момент імпульсу електрона відносно ядра в атомі
 або
або
 , (2)
, (2)
де
me
–
маса електрона,
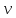 -
лінійна
швидкість електрона,
r
– відстань електрона до ядра.
-
лінійна
швидкість електрона,
r
– відстань електрона до ядра.
Це правило Бор розповсюдив на всі інші механічні системи, в тому числі і на атомну систему.
7. Напівквантова модель атома Бора
Згідно правилу квантування кругових орбіт Бора, можливі тільки ті орбіти з нескінченної кількості орбіт для яких виконується умова:
 .
(3)
.
(3)
Тут
число
 було названо
головним
квантовим числом.
було названо
головним
квантовим числом.
Хай
електрон рухається в полі атомного
ядра, заряд якого
 .
При
.
При
 - атом водню; при
- атом водню; при
 - воднеподібний іон, тобто атом у якого
залишився лише 1 електрон.
- воднеподібний іон, тобто атом у якого
залишився лише 1 електрон.
Рівняння руху електрона має вид
 - другий закон
Ньютона (4)
- другий закон
Ньютона (4)
Виключаючи
 з рівнянь (3) і (4) отримаємо вираз для
радіусів дозволених орбіт:
з рівнянь (3) і (4) отримаємо вираз для
радіусів дозволених орбіт:
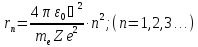 (5)
(5)
Радіус першої орбіти водневого атома називається Борівським радіусом:
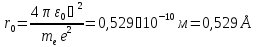
Значення
 добре узгоджується з його експериментальними
значеннями.
добре узгоджується з його експериментальними
значеннями.
Знайдемо
енергію яка відповідає радіусам атома
 .
Будемо вважати, що ядро нерухоме. Тоді
внутрішня енергія атома визначається
енергією електрона:
.
Будемо вважати, що ядро нерухоме. Тоді
внутрішня енергія атома визначається
енергією електрона:
 . (6)
. (6)
З рівняння (4) маємо
 .
.
Тоді

Враховуючи вираз (5) знайдемо дозволені значення внутрішньої енергії атома:
 (7)
(7)

Для атому водню Z = 1. Тоді різниця енергії двох рівнів
 . (8)
. (8)
А циклічна частота випромінювання:
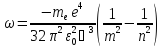 .
(9)
.
(9)
Або
 ,
(10)
,
(10)
де
 -
стала Рідберга (11)
-
стала Рідберга (11)
Це
значення
 з досить великою точністю співпадає з
значенням
з досить великою точністю співпадає з
значенням
 ,
знайденим з експерименту. А ф-ла (10)
співпадає з серіальною формулою Бальмера
(1), знайденою
емпірично.
,
знайденим з експерименту. А ф-ла (10)
співпадає з серіальною формулою Бальмера
(1), знайденою
емпірично.
8. Дослід Франка і Герца
Постулати Бора були підтверджені експериментально. Найбільш переконливе підтвердження існування дискретних енергетичних рівнів атома давали досліди Франка і Герца (1913р.). В цих дослідах вивчалася взаємодія електронів різної енергії з атомами ртуті. Схема досліду зображена на рисунку.
 UЗ
UЗ
U
К – підігрівний катод (джерело електронів)
С – анод, виконаний у вигляді сітки
А – металевий електрод (колектор)
U – прискорююча напруга
UЗ – затримуюча напруга
I – сила струму в гальванометрі
Вольт-амперна характеристика досліду представлена на наступному рисунку.

Якщо
енергія електронів менше 4,9 еВ то
спостерігається тільки пружна взаємодія
між електронами і атомами ртуті. Енергія
електронів майже не змінюється. Якщо
енергія електронів більше 4,9 еВ –
починається збудження атомів ртуті
внаслідок непружної взаємодії їх з
електронами, які передають їм свою
енергію. Збуджені атоми через
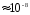 с
випромінюють фотони.
с
випромінюють фотони.
Дослід
Франка і Герца свідчить про те, що в
атомі ртуті різниця в енергії основного
стану і найближчого збудженого стану
дорівнює 4,9 еВ. Дослідження інших атомів
дало аналогічні результати. Наприклад
для калію
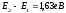 ;
для
;
для
 .
.
Пізніше
були поставлені досліди, які виявили в
атомах і інші енергетичні стани

